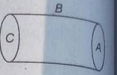
A hollow cylinder has a charge q C within it. It is the electric flux in unit of voltmeter associated with the curved surface B, the flum linked with the plane surface A in unit of V - m will be

The correct Answer is:A
Gauss' theorem states that the net electric flux through any closed surface is equal to the net charge inside the surface divided by .
Let electric flux linked with surfaces A, B and C be respectively. That is
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE EXERCISE (Exercise 2 (MISCELLANEOUS PROBLEMS))
47 Videos
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner
29 Videos
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner
29 Videos
- ELECTRONS AND PROTONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTRONS AND PROTONSEXERCISE - MHT CET CORNER
19 Videos
- FORCEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)
19 Videos
Similar Questions
A hollow cylinder has a charge qC within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B the flux linked with the plance surface A in unit of voltmeter will be

View SolutionA hollow cylinder has a charge qC within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B the flux linked with the plane surface A in unit of voltmeter will be

View Solution
Knowledge Check
A hollow cylinder has a charge qC within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B the flux linked with the plance surface A in unit of voltmeter will be
 A12(qε0−ϕ)Bq2ε0Cϕ3Dqε0−ϕ
A12(qε0−ϕ)Bq2ε0Cϕ3Dqε0−ϕA hollow cylinder has a charge qC within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B the flux linked with the plance surface A in unit of voltmeter will be
 A12(qε0−ϕ)Bq2ε0Cϕ3Dqε0=ϕ
A12(qε0−ϕ)Bq2ε0Cϕ3Dqε0=ϕA hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B, the flux linked with the plane surface A in unit of voltmeter will be
 A12(qε0−ϕ)Bq2ε0Cϕ3Dqε0−ϕ
A12(qε0−ϕ)Bq2ε0Cϕ3Dqε0−ϕ
A hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B, the flux linked with the plane surface A in unit of voltmeter will be

View SolutionA hollow cylinder has a charges q coulomb within it. If ϕ is the electric flux in units of V-m associated with the curved surface B, the flux linked with the plane surface A in units of V-m will be

View SolutionA hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux is unit of volt -m associated with the curved surface B, the flux linked with the plane surface A in the same units will be

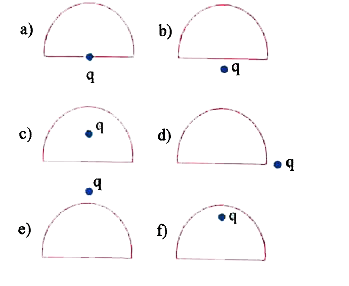
View SolutionFind the total flux due to charge qassociated with the given hemisphercal surface
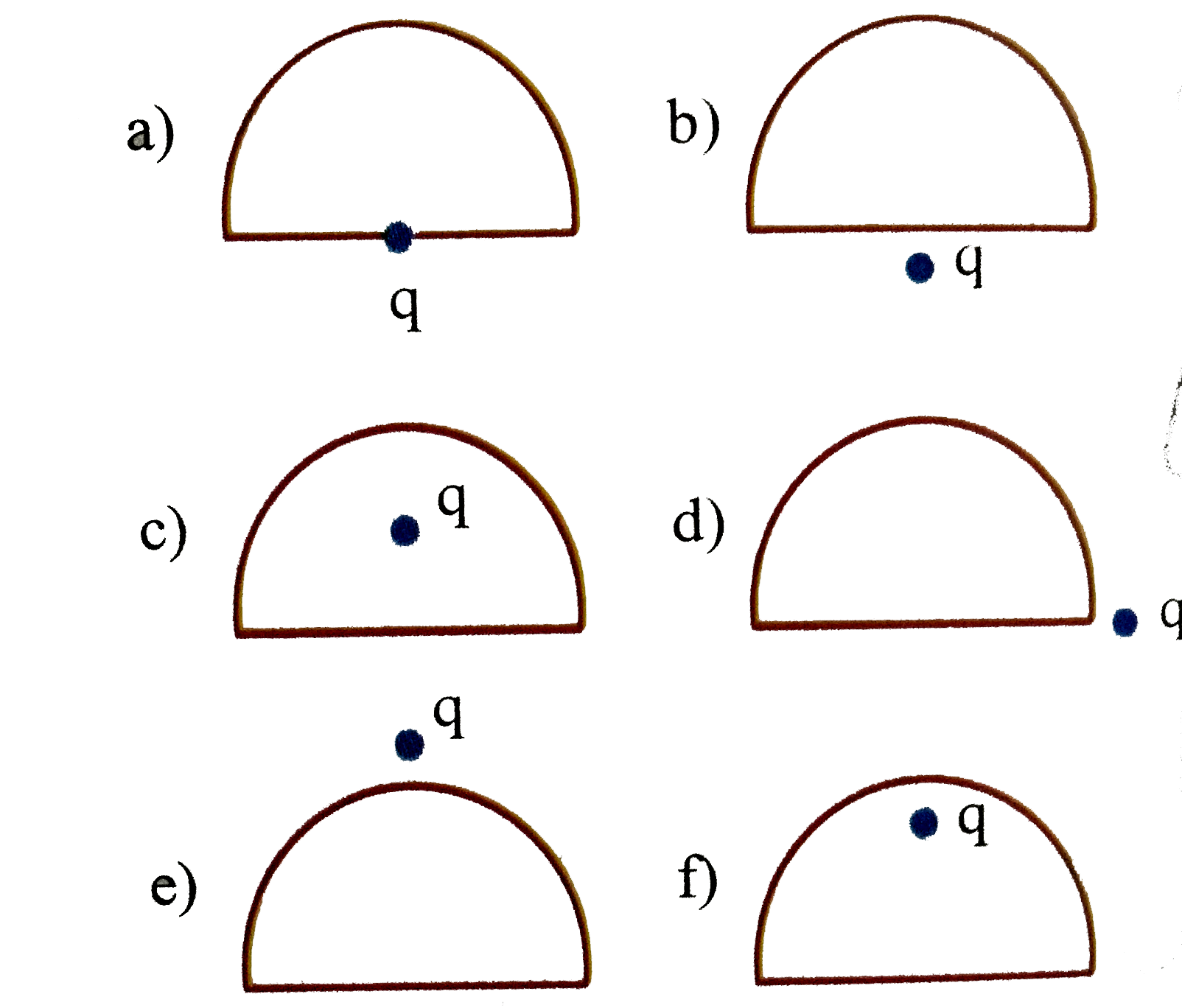
View SolutionFind the total flux due to charge q associated with the given hemispherical surface
View Solution
