How many 6μF,200V condensers are needed to make a condenser of 18μF,600?
9
18
3
27
The correct Answer is:D
To solve the problem of how many 6μF,200V capacitors are needed to create a capacitor of 18μF,600V, we can break it down into steps:
Step 1: Determine the configuration for voltage
To achieve a higher voltage rating of 600V, we need to connect capacitors in series. The voltage rating of capacitors in series adds up.
For 200V capacitors in series:
- If we connect n capacitors in series, the total voltage rating becomes n⋅200V.
To achieve 600V, we need:
\( n \times 200V = 600V \)
\( n = \frac{600V}{200V} = 3 \)
So, we need 3 capacitors in series to achieve 600V.
Step 2: Determine the equivalent capacitance for capacitors in series
The formula for the equivalent capacitance \( C_{eq} \) of capacitors in series is:
\( \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} \)
For 3 capacitors of 6μF:
\( \frac{1}{C_{eq}} = \frac{1}{6μF} + \frac{1}{6μF} + \frac{1}{6μF} = \frac{3}{6μF} \)
\( C_{eq} = \frac{6μF}{3} = 2μF \)
So, 3 capacitors in series give us an equivalent capacitance of 2μF at 600V.
Step 3: Determine how many sets of capacitors are needed for 18μF
Now, we need to achieve a total capacitance of 18μF. Since we have 2μF from the series combination, we can connect these combinations in parallel.
To find out how many 2μF capacitors are needed to make 18μF:
\( n \times 2μF = 18μF \)
\( n = \frac{18μF}{2μF} = 9 \)
So, we need 9 sets of 3∩aci→rs∈series to achieve 18μF.
Step 4: Calculate the total number of capacitors needed
Since each set consists of 3 capacitors, the total number of capacitors required is:
\( \text{Total capacitors} = 9 \times 3 = 27 \)
Thus, 27 capacitors of 6μF,200V are needed to create a capacitor of 18μF,600V.
Final Answer
The total number of 6μF,200V capacitors needed is 27.
---
To achieve a higher voltage rating of 600V, we need to connect capacitors in series. The voltage rating of capacitors in series adds up.
- If we connect n capacitors in series, the total voltage rating becomes n⋅200V.
\( n \times 200V = 600V \)
\( n = \frac{600V}{200V} = 3 \)
The formula for the equivalent capacitance \( C_{eq} \) of capacitors in series is:
\( \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} \)
For 3 capacitors of 6μF:
\( \frac{1}{C_{eq}} = \frac{1}{6μF} + \frac{1}{6μF} + \frac{1}{6μF} = \frac{3}{6μF} \)
\( C_{eq} = \frac{6μF}{3} = 2μF \)
Now, we need to achieve a total capacitance of 18μF. Since we have 2μF from the series combination, we can connect these combinations in parallel.
\( n \times 2μF = 18μF \)
\( n = \frac{18μF}{2μF} = 9 \)
Since each set consists of 3 capacitors, the total number of capacitors required is:
\( \text{Total capacitors} = 9 \times 3 = 27 \)
The total number of 6μF,200V capacitors needed is 27.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner
29 Videos
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE EXERCISE (Exercise 1 (TOPICAL PROBLEMS))
87 Videos
- ELECTRONS AND PROTONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTRONS AND PROTONSEXERCISE - MHT CET CORNER
19 Videos
- FORCEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)
19 Videos
Similar Questions
Minimum number of capacitors each of 8μF and 250 V used to make a composite capacitor of 16μF and 1000 V are
View SolutionThe capacity of a condenser A is 10μF and it is charged to a battery of 100 volt. The battery is disconnected and the condenser A is connected to a condenser B the common potential is 40V. The capacity of B is
View Solution
Knowledge Check
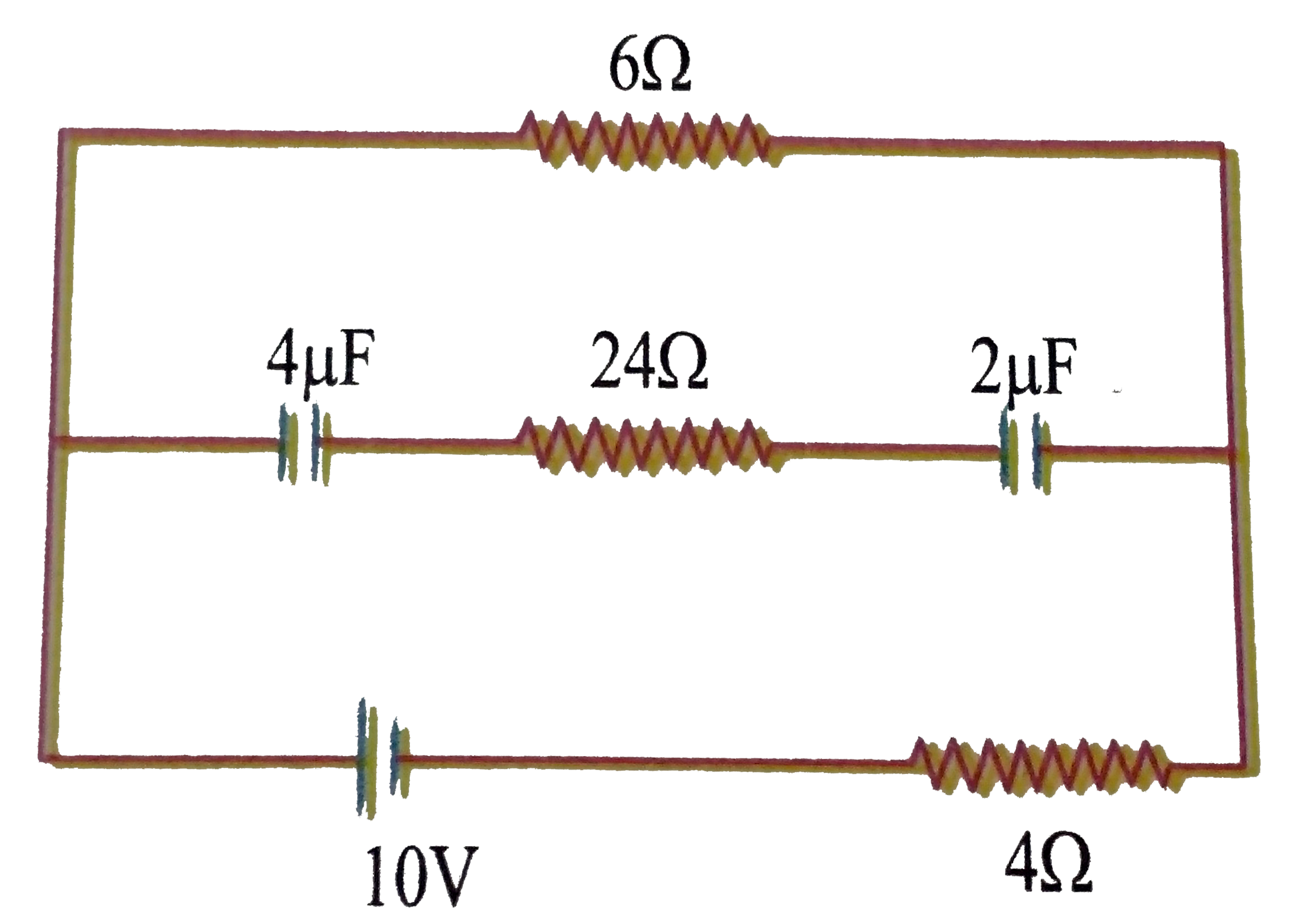
The charge developed on 4μF condenser isA18μCB4μCC8μCDzeroA condenser having a capacity of 6μF is charged to 100V and is then joined to an uncharged condenser of 14μF and then removed. The ratio of the charges on 6μF and 14μF and the potential of 6μF will be
A614 and 50 voltsB146 and 30 voltsC614 and 30 voltsD146 and 0 voltsA 4μF condenser is connected in parallel to another condenser of 8μF. Both the condensers are then connected in series with a 12μF condenser and charged to 20 volts. The charge on the plate of 4μF condenser is
A3.3μCB40μCC80μCD240μC
Two capacitors 3μF and 6μF are connected in series across a potential difference of 120V. Then the potential difference across 3μF capacitor is:
View SolutionA condenser of of capacity 2μF is charged to a potential of 100V. It is now connected to an uncharged condenser of capacity 3μF . The common potential will be
View SolutionA condenser A of capacity 4μF has a charge 20μC and another condenser B of capacity 10μF has a charge 40μC. If they are connected parallel, then
View SolutionA 4μF condenser is charged to 400V and then its plates are joined through a resistance of 1KΩ. The heat produced in the resistance is :
View SolutionThree capacitors of capacitance 3μF,10μF and 15μF are connected in series to a voltage source of 100V. The charge on 15μF is
View Solution
