Two identical parallel plate air capacitors are connected in series to a battery of emf V. If one of the capacitor is completely filled with dielectric material of constant K, then potential difference of the other capacitor will become
KV(K+1)
KVK+1
K−1KV
VK(K+1)
The correct Answer is:B
According the question, in first case (i.e. without dielectric)

For 2nd case when dielectric is inserted in one of the capacitor,

Given V1+V2=V
The capacitance of first capacitor becomes KC, So by charge conservation,
(KC)V1=CV2 ...(ii)
V1V2=1K
⇒ V1+V2V2=1+KK
⇒ V2=(KV1+K) (∵V1+V2=V)
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE EXERCISE (Exercise 2 (MISCELLANEOUS PROBLEMS))47videos
ELECTROSTATICS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTRONS AND PROTONSEXERCISE - MHT CET CORNER19videos
ELECTRONS AND PROTONS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)19videos
FORCE
Similar Questions
Two parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionTwo parallel plate air capacitance C, were connected in series to a battery with emf ξ. Then one of the capacitors was filled up with uniform dielectric with permittivity ε. How many times did the electric field strength in that capacitor decrease ? What amount of charge flows throgh the battery ?
View Solution
Knowledge Check
- Question 1 - Select One
Two parallel plate air capacitance of same capacity C are connected in series to a battery of emf E. Then one of the capacitors is completely filled with dielectric material of constant K. The change in the effective capacity of the series combination is
AC2[K−1K+1]B2C[K−1K+1]CC2[K+1K−1]DC2[K−1K+1]2 - Question 2 - Select One
Two identical parallel plate air capacitors are connected in series to a battery of emf V. If one of the capacitor is completely filled with dielectric material of constant K, then potential difference of the other capacitor will become
AK+1KV0BKK+1V0CK+12KV0D2KK+1V0 - Question 3 - Select One
Two identical parallel plate capacitors of capacitance C each are connected in series with a battery of emf, E as shown. If one of the capacitors is now filled with a dielectric of dielectric constant k, the amount of charge which will flow through the battery is (neglect internal resistance of the battery)
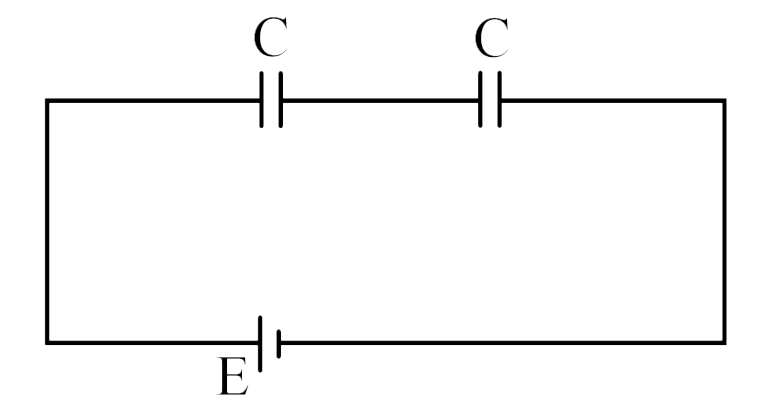 Ak+12(k−1)CEBk−12(k+1)CECk−2k+2CEDK+2k−2CE
Ak+12(k−1)CEBk−12(k+1)CECk−2k+2CEDK+2k−2CE
Two identical parallel plate capacitors are connected in parallel combination. Total charge on capacitors is Q0. If one of the capacitors is kept in a dielectric medium of constant K, then the total charge on both the capacitors will change to (P.D. across them is kept constant)
View SolutionTwo identical parallel plate capacitors are connected in series to a battery of 100V. A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capacitors will now be respectively
View SolutionTwo parallel plate capacitos of capacitences C and 2C are connected in parallel and charged to a potential difference V0 . The battery is then disconnected and the region between the plates of the capacitor C completely filled with a material of dielectric constant 2. The potential difference across the capacitors now becomes-
View SolutionTwo identical parallel plate capacitors are connected in parallel to a3 volt battery. The battery is disconnected and the two capacitors are joined in series, Fig. What is the potentail difference between A and B ?
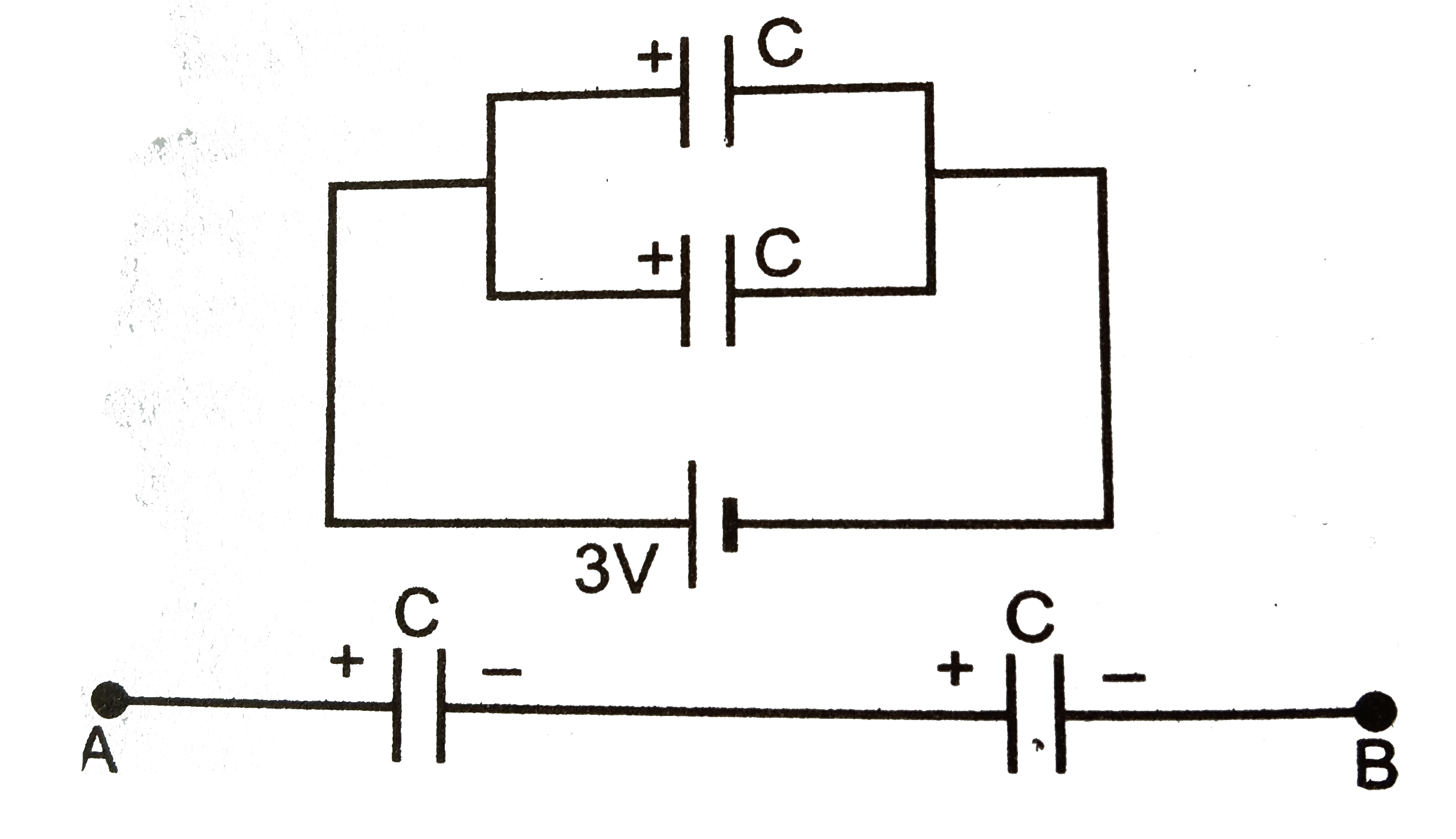 View Solution
View SolutionA parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
View Solution

