The rate constant of a reaction increases by 5% when its temperature is raised from $27^{\circ} c$ to $28^{\circ} c .$ The activation energy of the reaction is

$36.6 k J / m o l$

$16.6 k J / m o l$

$46.6 k J / m o l$

$26.6 k J / m o l$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To find the activation energy (EA) of the reaction given that the rate constant increases by 5% when the temperature is raised from 27°C to 28°C, we can use the Arrhenius equation in the form of the logarithmic relationship between the rate constants and temperatures.
1. Identify Given Values:
- Initial temperature (T1) = 27°C = 27 + 273 = 300 K
- Final temperature (T2) = 28°C = 28 + 273 = 301 K
- Rate constant at T1 (K1) = 100 (assuming an arbitrary value for simplicity)
- Rate constant at T2 (K2) = K1 + 5% of K1 = 100 + 5 = 105
2. Use the Arrhenius Equation:
The relationship between the rate constants and temperatures can be expressed as:
$log \frac{K 2}{K 1} = \frac{E A}{2.303 R} \cdot \frac{(T 2 - T 1)}{T 1 \cdot T 2}$
3. Substitute Known Values:
- $K 2 = 105$
- $K 1 = 100$
- $R = 8.314 J/mol K$
- $T 1 = 300 K$
- $T 2 = 301 K$
Substitute these values into the equation:
$log \frac{105}{100} = \frac{E A}{2.303 \cdot 8.314} \cdot \frac{(301 - 300)}{300 \cdot 301}$
4. Calculate the Logarithm:
$log \frac{105}{100} = log 1.05 \approx 0.02119$
5. Calculate the Temperature Difference and Product:
$T 2 - T 1 = 301 - 300 = 1 K$
$T 1 \cdot T 2 = 300 \cdot 301 = 90300 K^{2}$
6. Substitute Values into the Equation:
$0.02119 = \frac{E A}{2.303 \cdot 8.314} \cdot \frac{1}{90300}$
7. Rearranging to Solve for EA:
$E A = 0.02119 \cdot 2.303 \cdot 8.314 \cdot 90300$
8. Calculate EA:
- First calculate $2.303 \cdot 8.314 \approx 19.1$
- Then calculate $0.02119 \cdot 19.1 \approx 0.404$
- Finally, $E A \approx 0.404 \cdot 90300 \approx 36465.2 J/mol \approx 36.5 kJ/mol$
9. Final Result:
The activation energy (EA) of the reaction is approximately 36.65 kJ/mol.

Updated on:7/8/2024

Class 12 CHEMISTRY CHEMICAL KINETICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
When the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes $K$ as a function of temperature, i.e.
$k = A e_{a}^{- E_{a} / R T}$
where
$k =$ rate constant
$A =$ a constant (frequency factor)
$E_{a} =$ energy of activation
${log}_{10} k = {log}_{10} A - \frac{E_{a}}{2.303 R} [\frac{1}{R}]$
$Y = C + M X$
It is the equation of straight line with negative slope. On plotting ${log}_{10} k$ against $[\frac{1}{T}]$ we get a straight line as shown below :

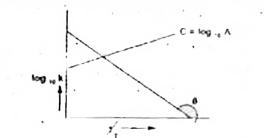
The slope gives activation energy and intercept gives frequency factor.
Also $log . \frac{k_{2}}{k_{1}} = \frac{E_{a}}{2.303} [\frac{T_{2} - T_{1}}{T_{1} T_{2}}]$
The rate constant of a reaction is increased by $5 %$ when its temperature is raised from $27^{\circ} C$ to $28^{\circ} C$ . The activation energy of the reaction in kJ/mol is
A $36.6$
B $16.6$
C $46.6$
D $26.6$
Question 2 - Select One
The rate of a reaction becomes 4 times when temperature is raised from 293 K to 313 K. The activation energy for such reaction would be
A50.855 kJ ${mol}^{- 1}$
B52.849 kJ ${mol}^{- 1}$
C54.855 kJ ${mol}^{- 1}$
D56.855 kJ ${mol}^{- 1}$
Question 3 - Select One
A particular reaction rate increases by a a factor of five when the temperature is increased from $5^{\circ}$ to $27^{\circ}$ C. What is the activation energy of the reaction?
A6.10 KJ . ${mol}^{- 1}$
B18.9 KJ . ${mol}^{- 1}$
C50.7 KJ . ${mol}^{- 1}$
D157 KJ . ${mol}^{- 1}$

The rate constant of a reaction increases by 5% when its temperature is raised from $27^{\circ} c$ to $28^{\circ} c .$ The activation energy of the reaction is

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

The rate of a reaction becomes 4 times when temperature is raised from 293 K to 313 K. The activation energy for such reaction would be

A particular reaction rate increases by a a factor of five when the temperature is increased from $5^{\circ}$ to $27^{\circ}$ C. What is the activation energy of the reaction?

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-CHEMICAL KINETICS -Exercise 2

The rate constant of a reaction increases by 5% when its temperature is raised from 27∘c to 28∘c. The activation energy of the reaction is

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

The rate of a reaction becomes 4 times when temperature is raised from 293 K to 313 K. The activation energy for such reaction would be

A particular reaction rate increases by a a factor of five when the temperature is increased from 5∘ to 27∘ C. What is the activation energy of the reaction?

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-CHEMICAL KINETICS -Exercise 2

The rate constant of a reaction increases by 5% when its temperature is raised from $27^{\circ} c$ to $28^{\circ} c .$ The activation energy of the reaction is

A particular reaction rate increases by a a factor of five when the temperature is increased from $5^{\circ}$ to $27^{\circ}$ C. What is the activation energy of the reaction?