An object has velocity →v1 w.r.t. ground. An observer moving with constant velocity →v0 w.r.t. ground measures the velocity of the object as →v2. The magnitudes of three velocities are related by
v0≥v1+v2
v1≤v2+v0
v2≥v1+v0
All of the above
The correct Answer is:B
b. →v2=→v1−→v0,→v2+→v0=→v1
From the law of triangle, we can draw the
velocity vector diagram.
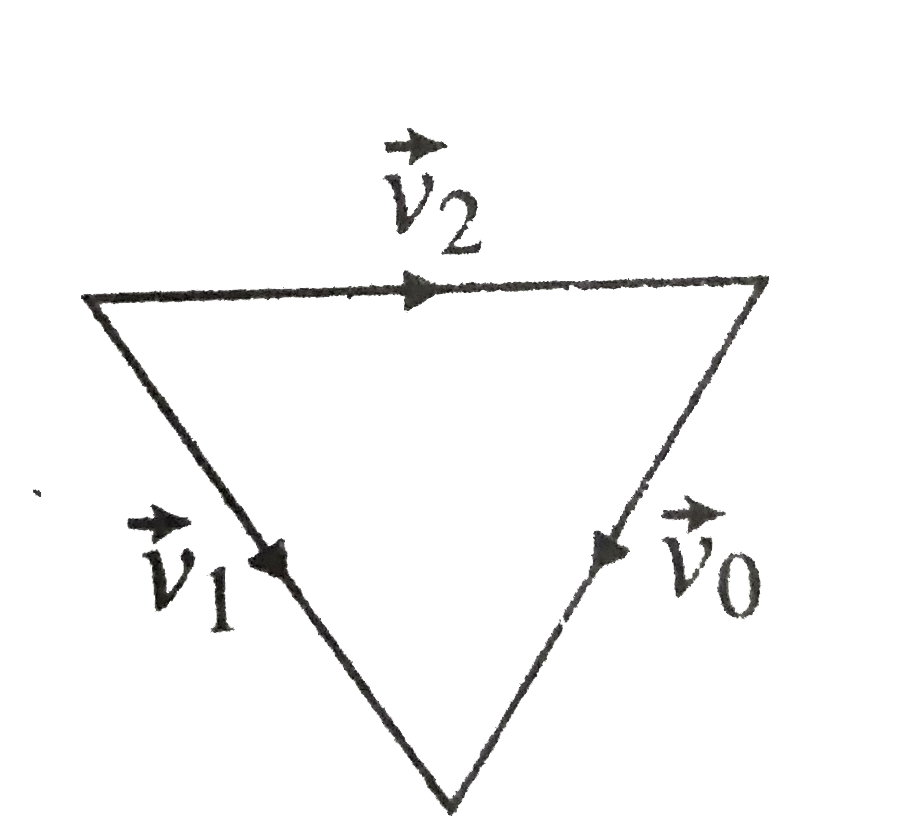
From triangle property, sum of two sides gethird
side. So v1≤v0+v2 .
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type26videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type35videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type9videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
Similar Questions
Knowledge Check
- Question 1 - Select One
The velocity of image w.r.t ground in the below figure is
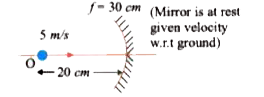 A45 m/s and approaches the mirrorB45 m/s and moves away from the mirrorC60 m/s and approaches the mirrorD60 m/s and moves away from the mirror
A45 m/s and approaches the mirrorB45 m/s and moves away from the mirrorC60 m/s and approaches the mirrorD60 m/s and moves away from the mirror - Question 2 - Select One
A particle moving with velocity →V is acted by the three forces shown by the vector triangle PQR. The velocity of the particle will :
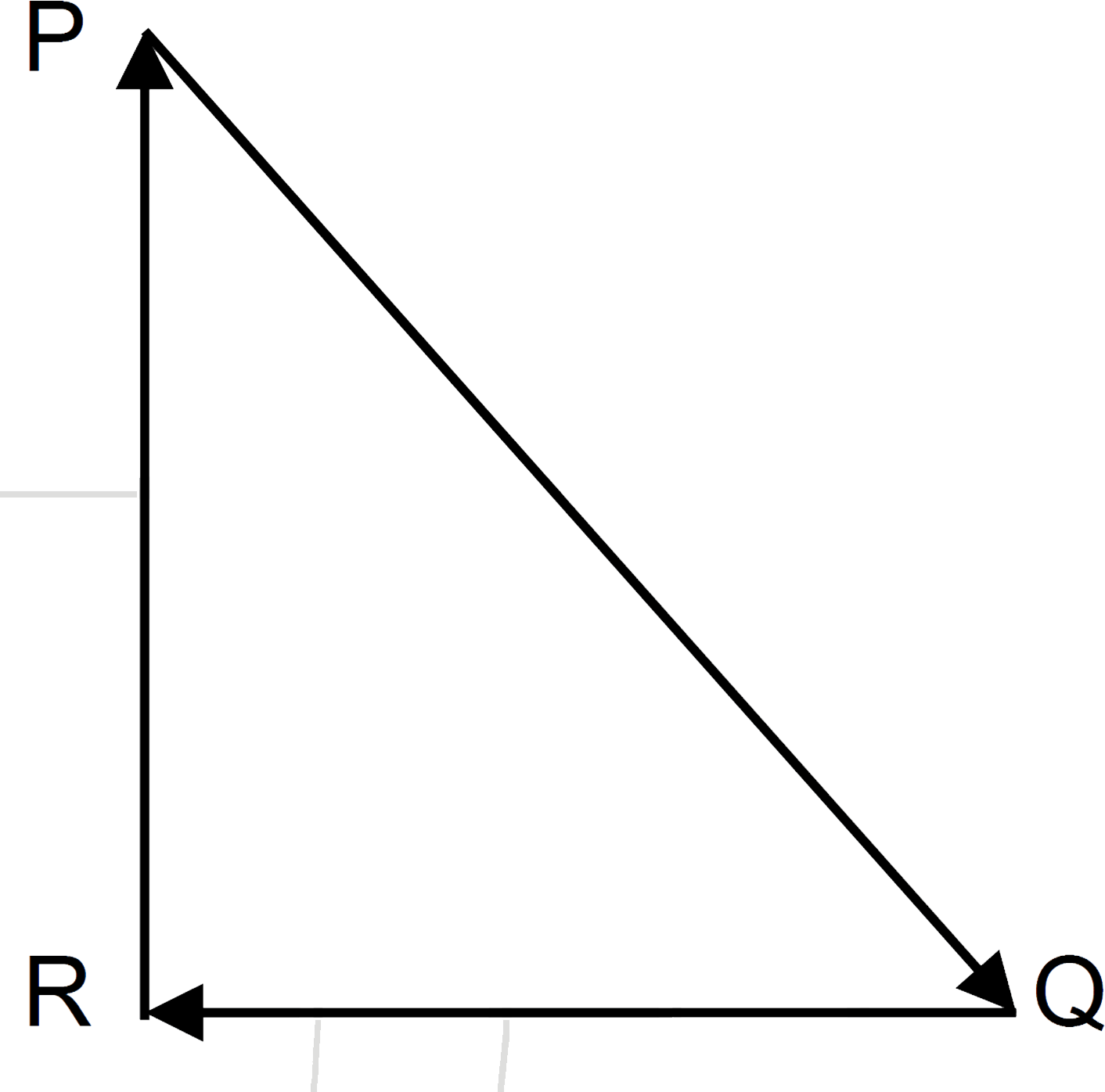 AIncreaseBDecreaseCRemain constantDChange according to the smallest force
AIncreaseBDecreaseCRemain constantDChange according to the smallest force - Question 3 - Select One
A bird is flying towards south with a velocity 40km/h and a train is moving with a velocity 40 km/h towards east. What is the velocity of the bird w.r.t. an obserber in the train ?
A40√2km/h. N-EB40√2km/h. S-EC40√2 km/h. S-WD40√2 km/h. N-W
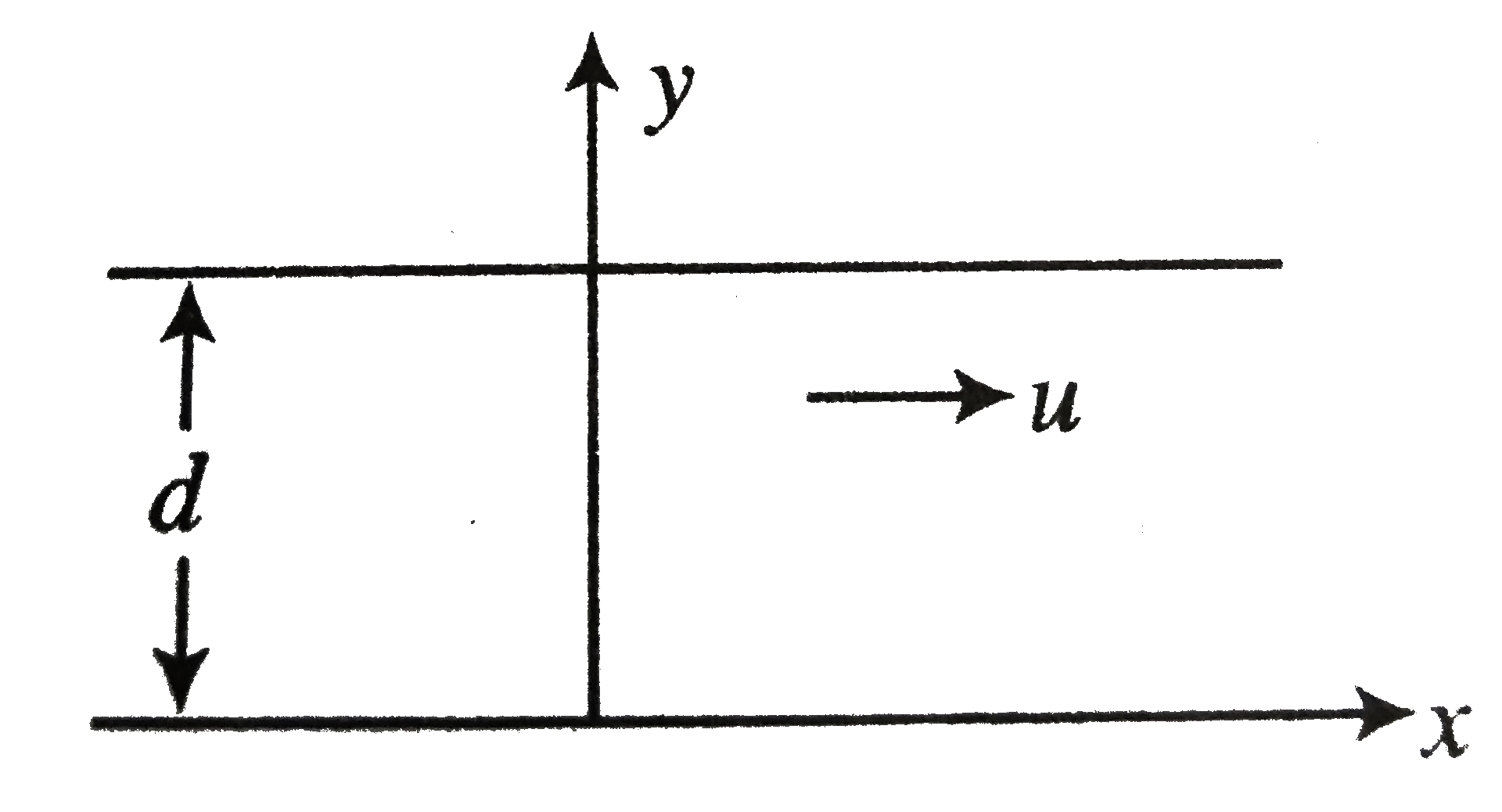
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
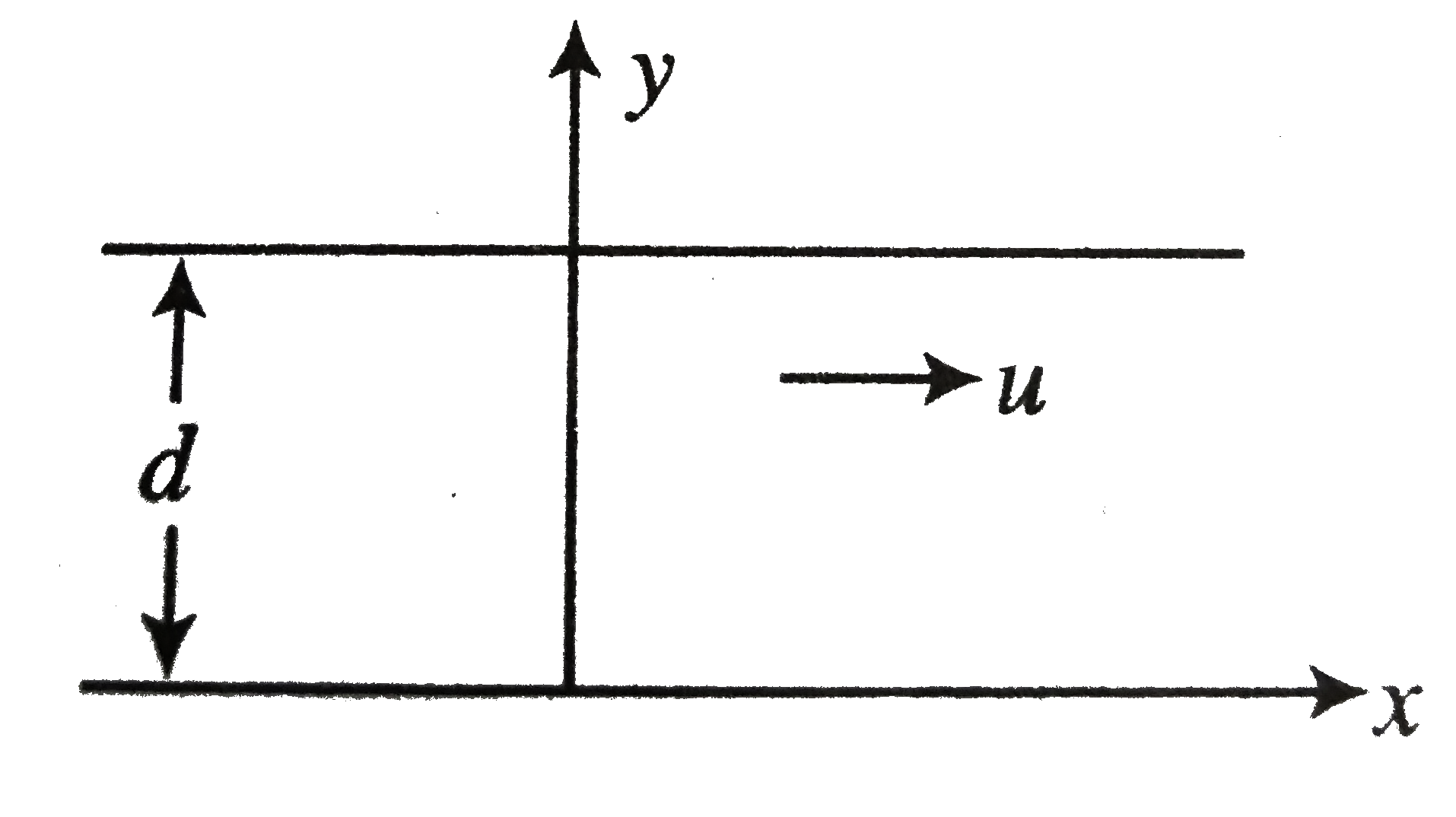
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View SolutionThe velocity varies with time as →v=aˆi+btˆj , where a and b are positive constants. The magnitude of instantaneous velocity and acceleration would be
View Solution