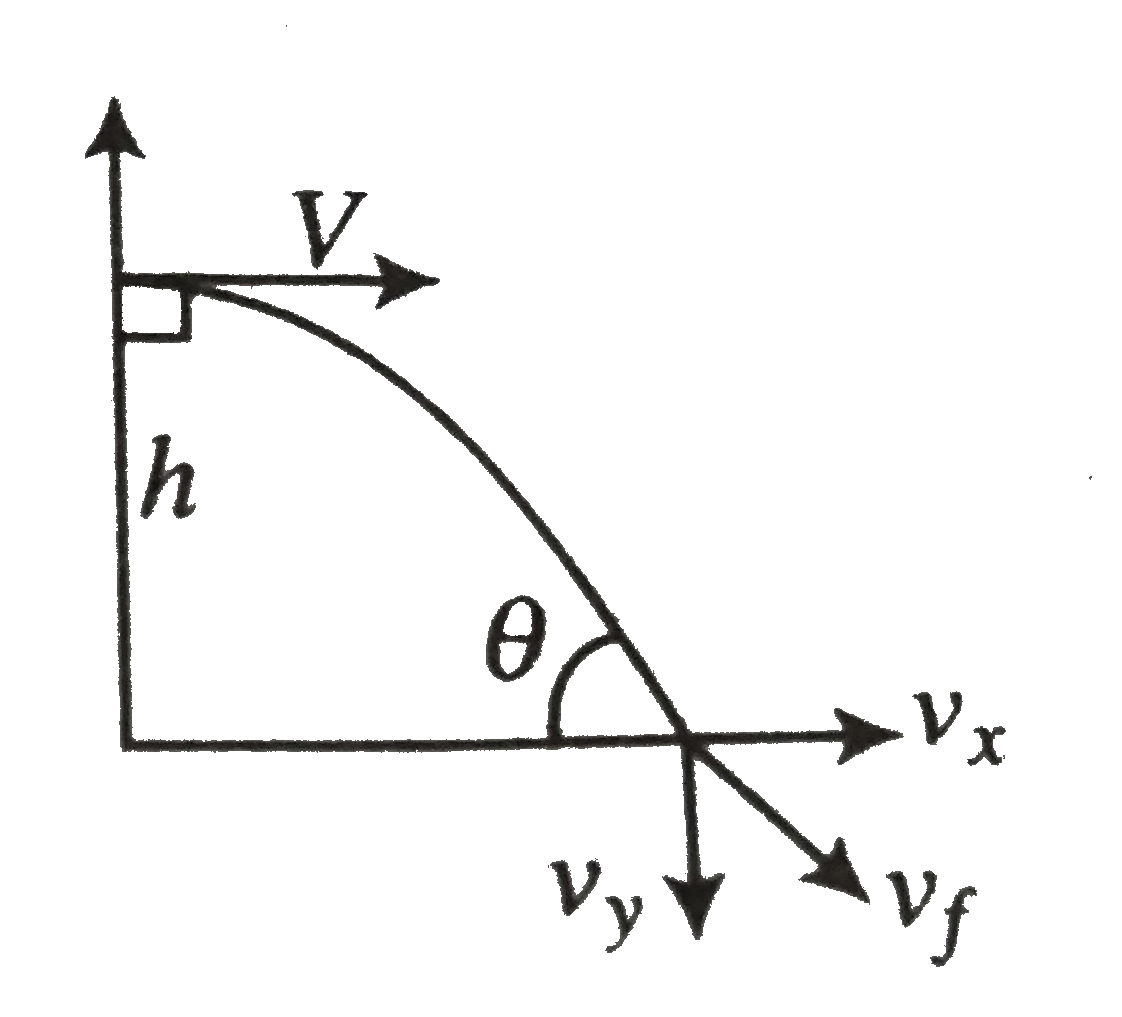
A student throws soft balls out of the window at different angles to the horizontal. All soft balls have the same initial speed v=10√3ms−1. It turns out that all soft balls landing velocities make angles 30∘ or greater with the horizontal. Find the height h (in m) of the window above the ground.
The correct Answer is:5
Minimum θ implies minimum Vfy and maximum Vfx.
In order to have the aforementioned situation, the rock has to
be launched horizontally.
vy=√2gh
tan30∘=vyv=√2×10×h10√3,h=5m
 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks4videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - True or False2videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type35videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type9videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
Similar Questions
(a) A boy throws several balls out of the window of his house at different angles to the horizontal. All balls are thrown at speed u=10m/s and it was found that all of them hit the ground making an angle of 45° or larger than that with the horizontal. Find the height of the window above the ground [take g=10m/s2]
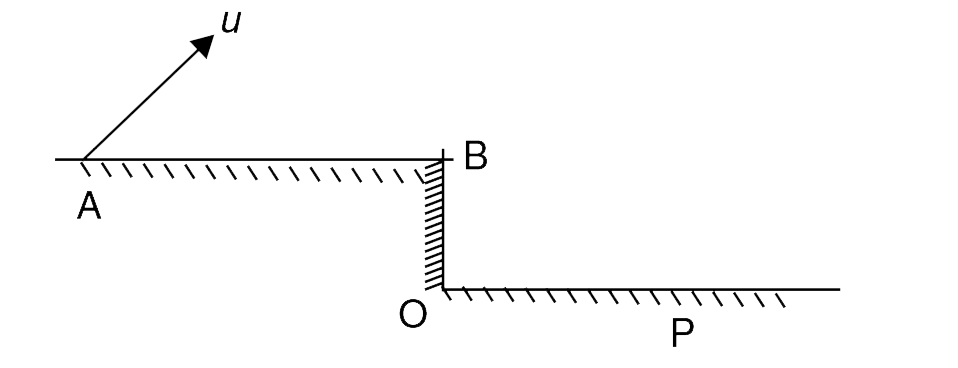
(b) A gun is mounted on an elevated platform AB. The distance of the gun at A from the edge B is AB=960m. Height of platform is OB=960m. The gun can fire shells with a velocity of u=100m/s at any angle. What is the minimum distance (OP) from the foot of the platform where the shell of gun can reach ?
 View Solution
View SolutionA player kicks a ball at an angle of 37∘ to the horizontal with an initial speed of 15ms−1 . Find its time of fight.
View Solution
Knowledge Check
- Question 1 - Select One
A ball is thrown upwards at an angle of 60∘ to the horizontal. It falls on the ground at a distance of 90 m . If the ball is thrown with the same initial velocity at an angle 30∘, it will fall on the ground at a distance of
A30mB60mC90mD120m - Question 2 - Select One
A football player throws a ball with a velocity of 50 metre/sec at an angle 30 degrees from the horizontal. The ball remains in the air for (g=10m/s2)
A2.5secB1.25secC5secD0.625sec - Question 3 - Select One
A particle at a height h from the ground is projected with an angle 30∘ from the horizontal, it strikes the ground making angle 45∘ with horizontal. It is again projected from the same point with the same speed but with an angle of 60∘ with horizontal. Find the angle it makes with the horizontal when it strikes the ground
Atan−1(4)Btan−1(5)Ctan−1(√5)Dtan−1(√3)
A ball is projected at an angle of 30∘ above with the horizontal from the top of a tower ans strikes the ground in 5sec at angle of 45∘ with the horizontal. Find the hieght of the lower and the speede with which it was projected.
View SolutionA ball is projected at an angle of 30∘ above with the horizontal from the top of a tower ans strikes the ground in 5sec at angle of 45∘ with the horizontal. Find the hieght of the lower and the speede with which it was projected.
View SolutionA football player kicks a ball at an angle of 37∘ to the horizontal with an initial speed of 15ms−1. Assuming that the ball travels in a vertical plane, calculate the maximum height reached.
View SolutionA ball moving is thrown at an angle of 60∘ with the horizontal , with initial speed of 30m/s . Calculate
(a) time of flight of the ball
(b) hrizontal range .
(c) maximum height attained .View SolutionA ball is thown at angle θ and another ball is thrown at angle (90∘−θ) with the horizontal direction from the same point each with speeds of 40 m/s. The second ball reaches 50 m higher than the first ball. Find the individual heights. g=10m/s2
View Solution

