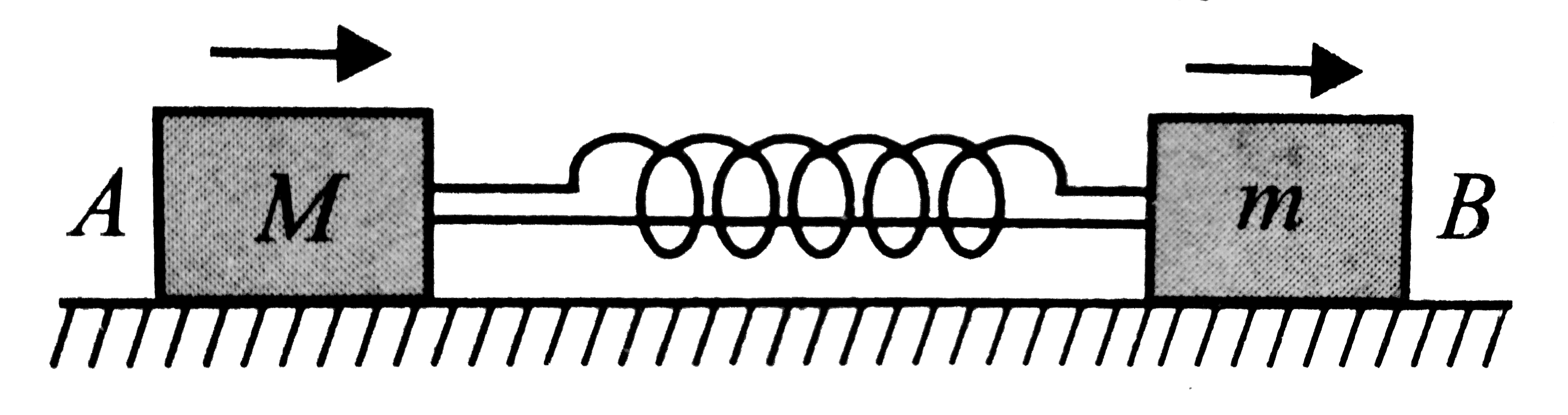
Block A of massM=2kg is connected to another block B of mass m=1kg with a string and a spring of force constant k=600N/m as shown in Fig. Initially, spring is compressed to 10cm and whole system is moving on a smooth surface with a velocity v=1m/s. At any time, thread is burnt, the velocity of block A, when B is having maximum velocity w.r.t. ground, is
zero
1m/S
3m/s
none of these
The correct Answer is:C
The velocity of B will be maximum when spring comes to its natural length. Let at the at time their velocities are v1 and v2 as shown

Conservation of momentum,
2v1+1v2(2+1)×1⇒2v1+v2=3…..i
Conservation of energy
122v21+121v22=12600(10100)2=123(1)2⇒2v21+v22=9
From eqn i and ii
v1=2m/s,v2=−1m/s or v1=0,v2=3m/s
The second solution is possible.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View Solution
Knowledge Check
A block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
A(a) MF(m+M)B(b) mFMC(c) (M+m)FmD(d) mF(m+M)A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
AMF(m+M)BmFMC(M+m)FmDmF(m+M)
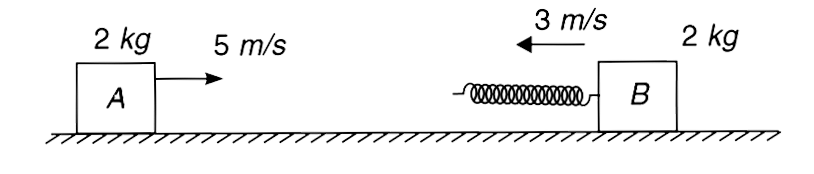
A block A of mass 2kg is moving to right with a speed of 5 m/s on a horizontal smooth surface. Another block B of mass 2 kg, with a mass less spring of force constant K=200 N/m attached to it, is moving to left on the same surface with a speed of 3 m/s. Block A collides with the spring attached to B. Calculate
(a) the final velocity of the block A.
(b) the minimum kinetic energy of the system of two blocks during subsequent motion.
(c) Repeat part (b) if there is no spring and the two blocks collide head on. Assume that the blocks are made of perfectly elastic material
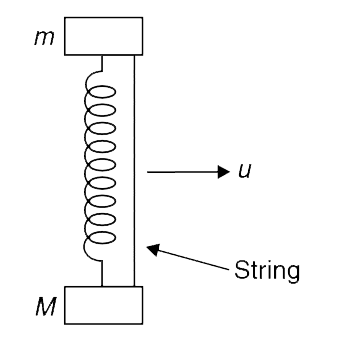
View SolutionTwo blocks of masses m=2kgandm=8kg are connected to a spring of force constant K=1kN/m. The spring is compressed by 20cm and the two blocks are held in this position by a string. The system is placed on a horizontal smooth surface and given a velocity u=3m/s perpendicular to the spring. The string snaps while moving. Find the speed of the block of mass m when the spring regains its natural length.
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is upstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solution
