A block of mass m starts from rest and slides down a frictionless semi-circular track from a height h as shown. When it reaches the lowest point of the track, it collides with a stationary piece of putty also having mass m. If the block and the putty . stick together and continue to slide, the maximum height that the block-putty system could reach is
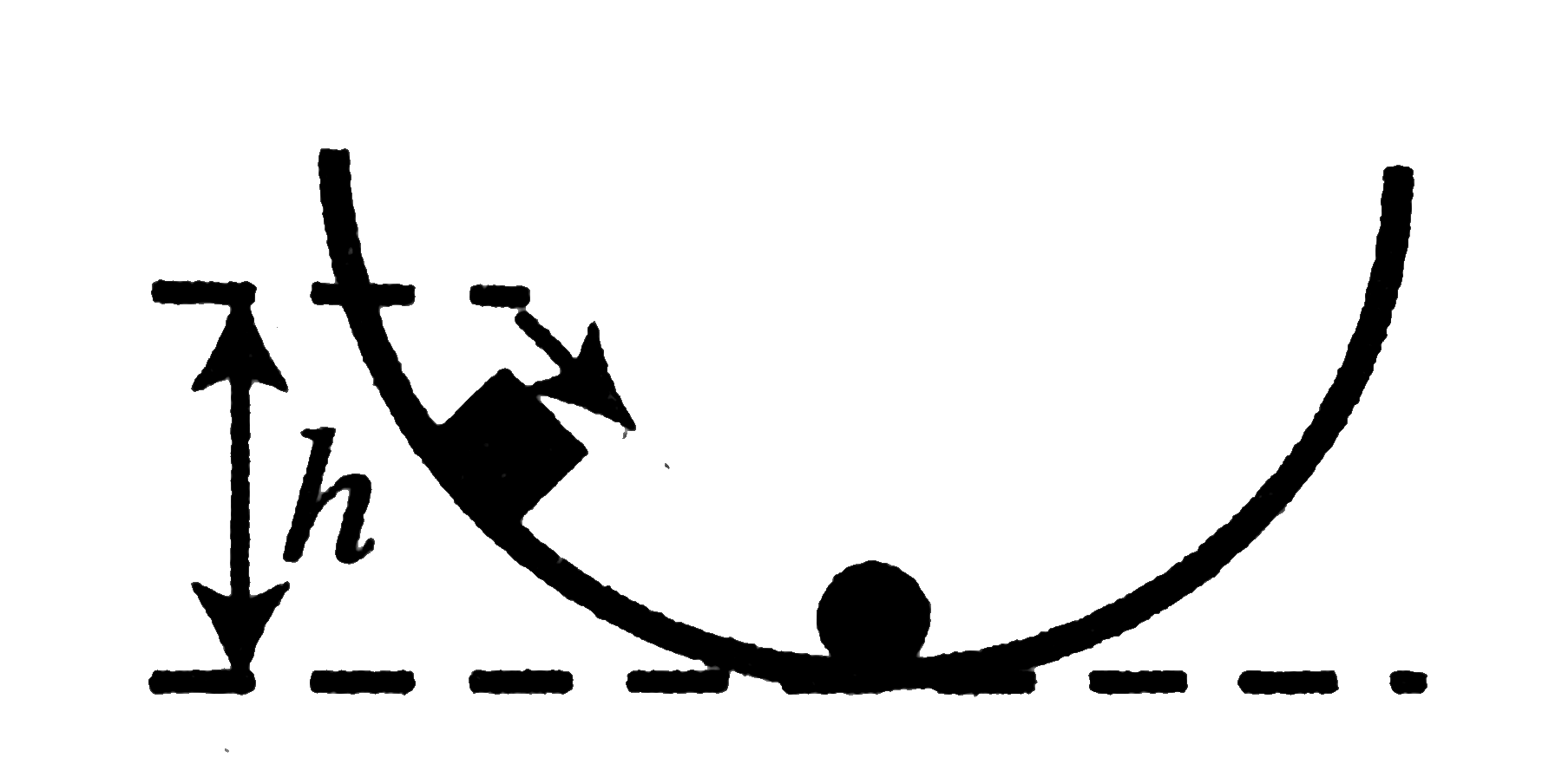
h4
h2
h
independent of h
The correct Answer is:A
v0=√2gh before collision
Applying conservation principe of mometum,
mv0=(m+m)u
∴u=v02
Applying conservation principle of momentum,
12(2m)u2=2mgh'
∴h'=u22g⇒h'=v208g
h'=(2gh)/(8g)impliesh'=h/4
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Knowledge Check
- Question 1 - Select One
A small object of mass m starts from rest at the position shown and slides along the fricationless loop-the -loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
 AR/4BR/2CRD2R
AR/4BR/2CRD2R - Question 2 - Select One
A small of mass m starts from rest at the position shown and slides along the frictionless loop the loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
 AR/2BRCR/4D3R/4
AR/2BRCR/4D3R/4 - Question 3 - Select One
A mass m starting from A reaches B of a frictionless track. On reaching B, it pushes the track with a force equal to x times its weight, then the applicable relation is
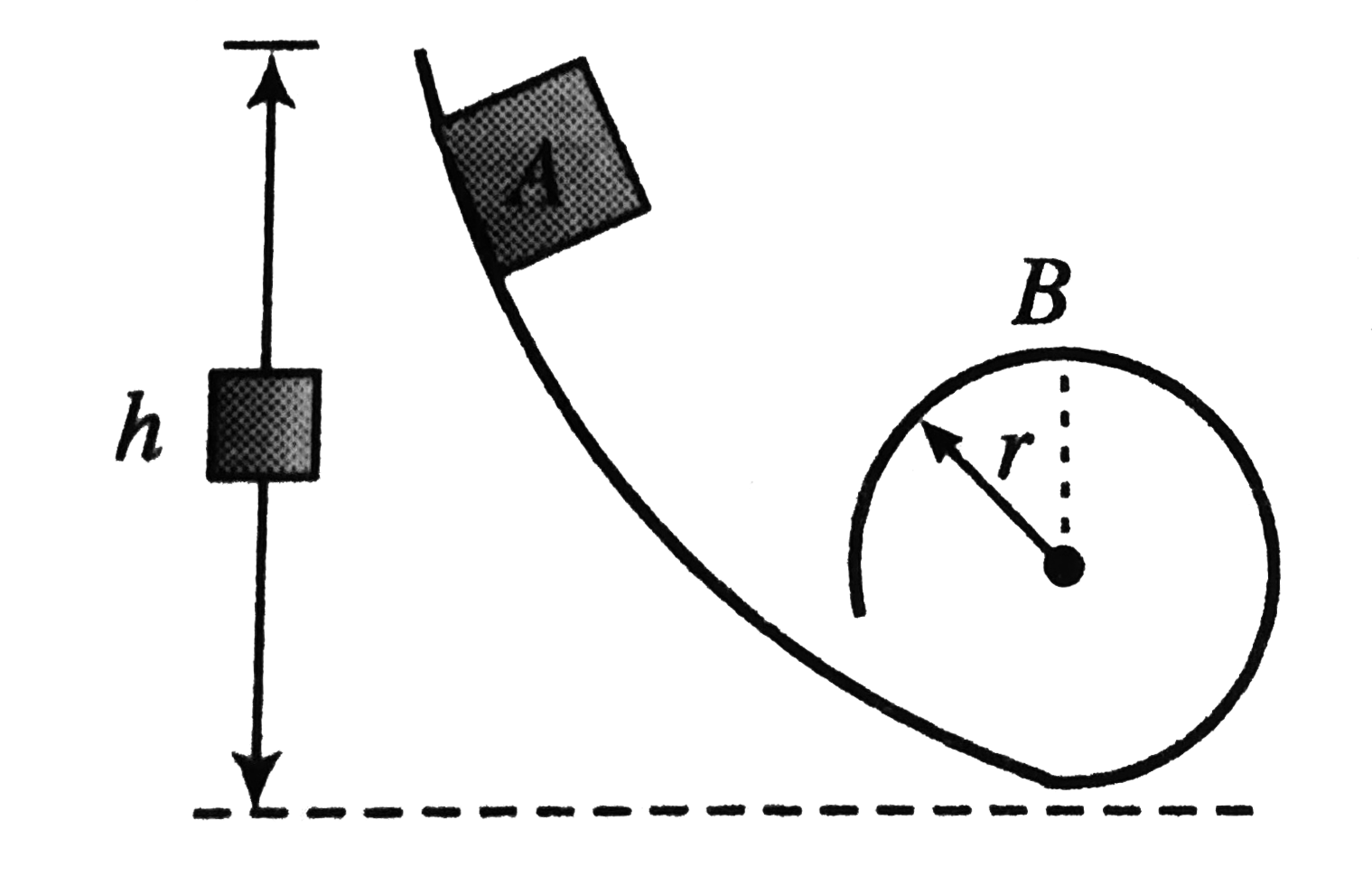 A(a) h=(x+5)2rB(b) h=x2rC(c) h=rD(d) h=(x+12)r
A(a) h=(x+5)2rB(b) h=x2rC(c) h=rD(d) h=(x+12)r
A block of mass m slides along a frictionless surfce as shown in the figure. If it is releases from rest t A what is its speed at B?
 View Solution
View SolutionA block of mass m is lying at rest at point P of a wedge having a smooth semi-circular track of radius R. What should be the minimum value of a0 so that the mass can just reach point Q
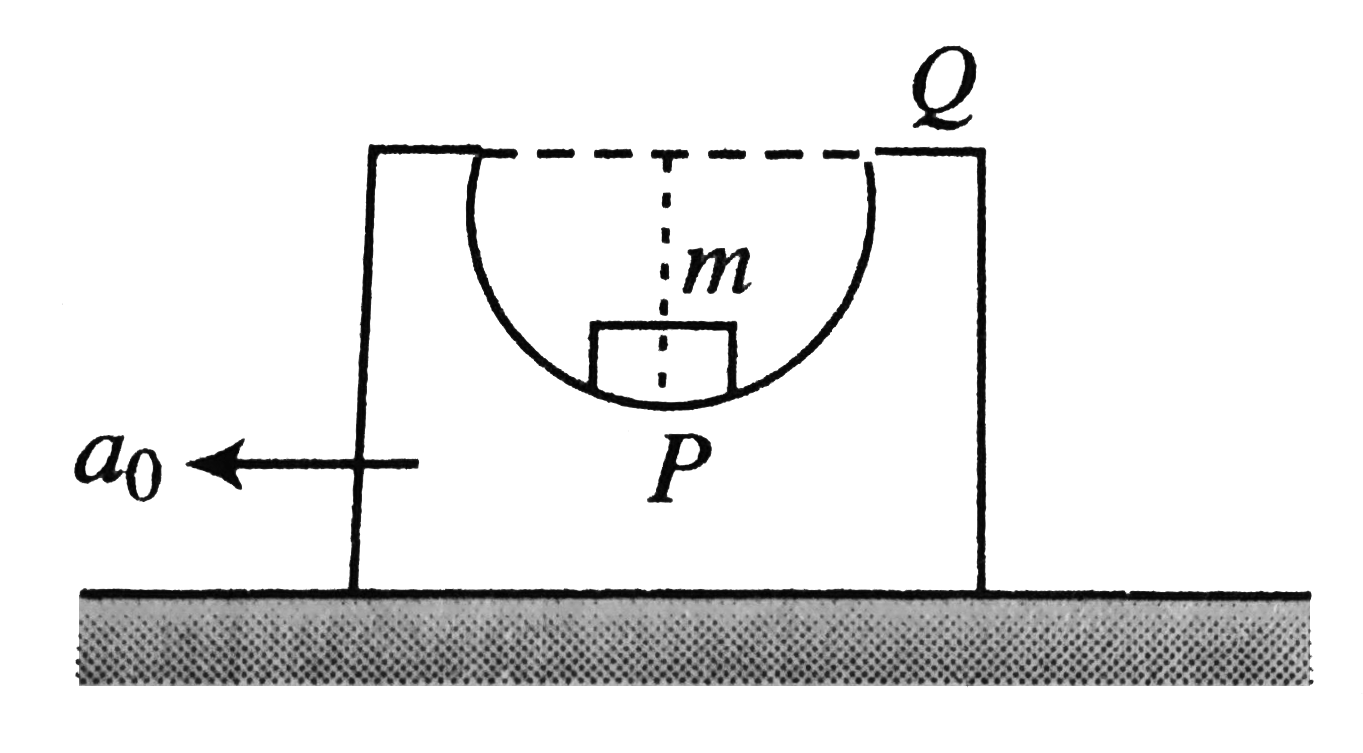 View Solution
View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-
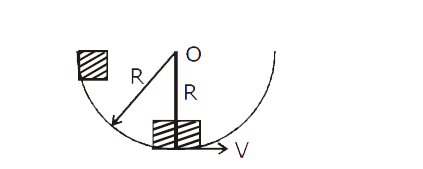 View Solution
View SolutionA block of mass m is released from a height R on the frictionless incline as shown. The incline leads to a circle of radius R/2. The maximum height attained by the block is
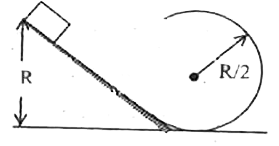 View Solution
View SolutionA block slides down a curved frictionless track and then up an inclined plane as in figure. The coefficient of kinetic friction between the block and incline is μk. Find the maximum height reached by the clock.
 View Solution
View Solution

