A pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
What is the momentum transferred to the bob by the bullet?
mv
mv2
Mv2
Mv
The correct Answer is:B

Momentum lost by the bullet =mv−mv2=mv2
This will be transferred to the bob.
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Integer
Explore 16 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Fill In The Blanks
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A simple pendulum of length 1m has a wooden bob of mass 1kg. It is struck by a bullet of mass 10g moving with a speed of 200m/s. The bullet gets embedded into the bob. Obtain the height to which the bob rises before swinging back.
Take g=10m/s2.
View SolutionThe wooden bob of a simple Pendulum of length 1 m is struck by a bullet of mass 10−3 kg moving with a speed of 300 m s−1 . If the bullet gets embedded into the bob then calculate the height to which the bob will rise before going back to mean position. The mass of bob is 0.8 kg .
View Solution
Knowledge Check
A pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob is just able to complete the circular motion, then tension at the lowest point just when the bob starts rising will beA6MgB5MgC3MgDMgA pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob stops where the string becomes horizontal then v isA2Mm√3glB2Mm√5glC2Mm√glD2Mm√2glA pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
A3m2m1√5glBm1m√5glC2m3m1√5glDm1m√gl
A pendulum consists of a wooden bob of mass in and of length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed (v1)/3 and the bob just completes motion along a vertical circle. Then v1is
View SolutionA pendulum consists of a wooden bob of mass m and of length L. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed v1/3 and the just completes motion along a vertical circle. Then v1 is:
View SolutionA pendulum comsists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1 and it emerges from the bob with speed v13. The bob just completes motion along a vertical circle. Then v1 is
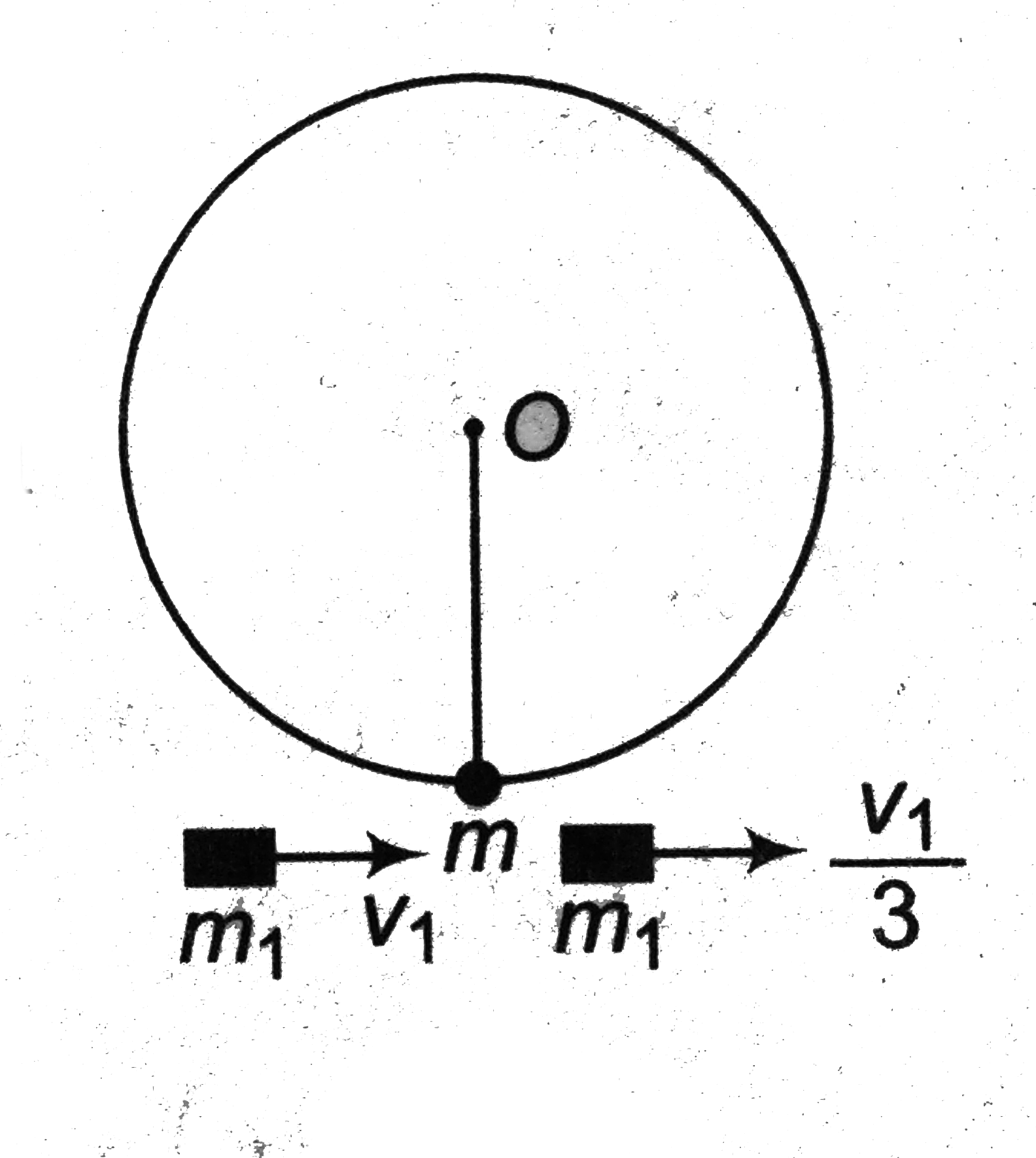
View SolutionA simple pendulum of length 1 m has a wooden bob of mass 1 kg. It is struck by a bullet of mass 10−2 kg moving with a speed of 2×102m/s. The bullet get embedded into the bob. Find the height to which the bob rises before swinging back.
View SolutionA small ball of mass m collides elastically with a simple pendulum with bob of mass ma at rest. The macimum height attained by the bob after collision is
View Solution