Look at the drawing given in the figure which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is m. The mass of the ink used to draw the outer circle is 6m.
The coordinates of the centres of the different parts are: outer circle (0,0), left inner circle (−a,a), right inner circle (a,a), vertical line (0,0) and horizontal line (0,−a). The y-coordinate of the centre of mass of the ink in this drawing is
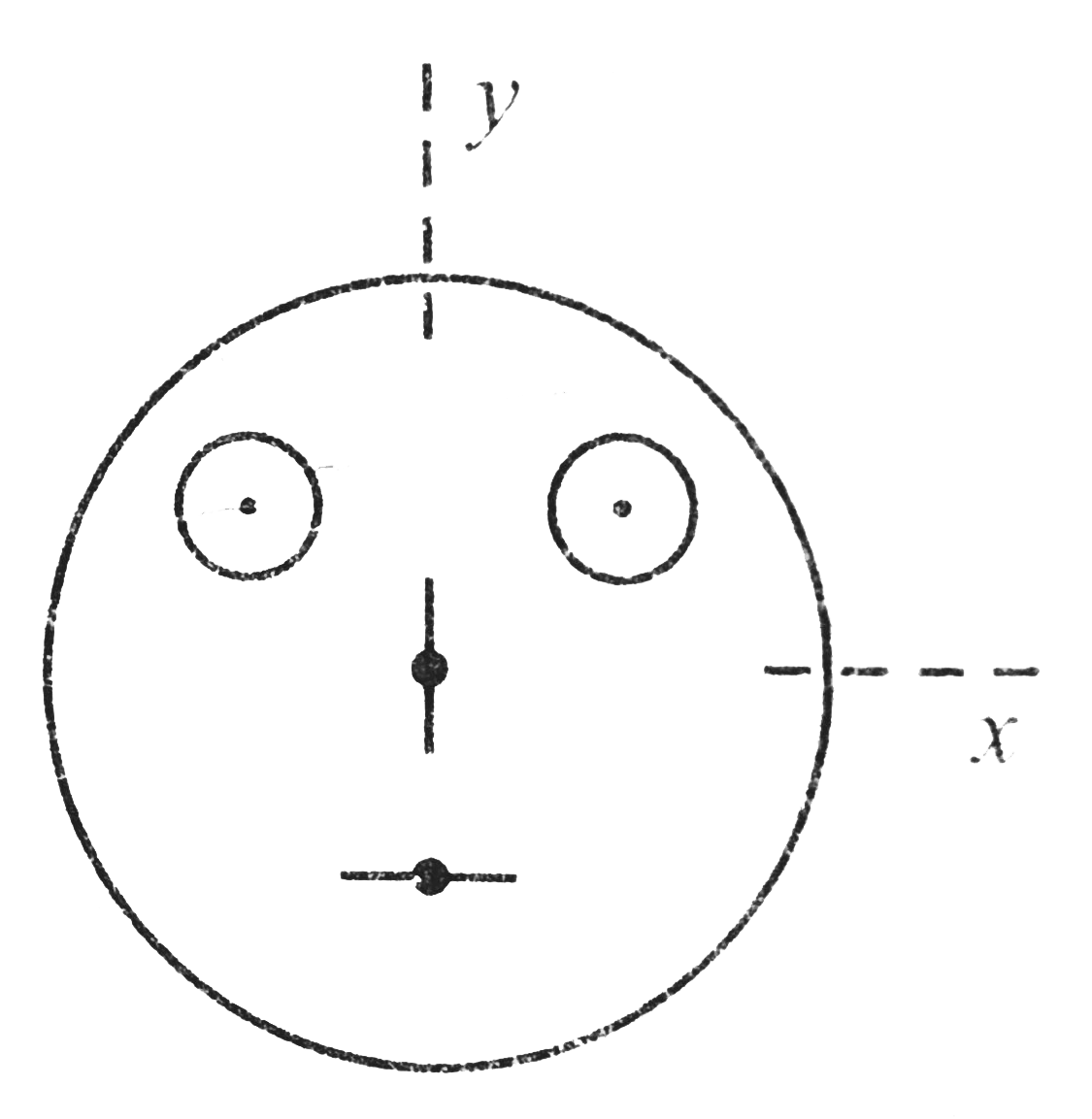
A
a10
B
a8
C
a12
D
a3
Video Solution
Text Solution
The correct Answer is:A
YCM=6m×0+m×a+m×a+m×0++m×(−a)10m

YCM=a10
|
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - MCQ_TYPE
4 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - AR_TYPE
1 Video
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Knowledge Check
Look at the drawing given in the figure which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is m. The mass of the ink used to draw the outer circle is 6 m. The coordinates of the centres of the different parts are: outer cicle (0,0), left circle (-a, a), right inner circle (a,a), vertical line (0,0) and horizontal line (0 ,-a). The y-coordinate of the centre of mass of the ink in this drawing is
 Aa10Ba8Ca12Da3
Aa10Ba8Ca12Da3In the figure, when the outer circles all have radii 'r', then the radius of the inner circle will be
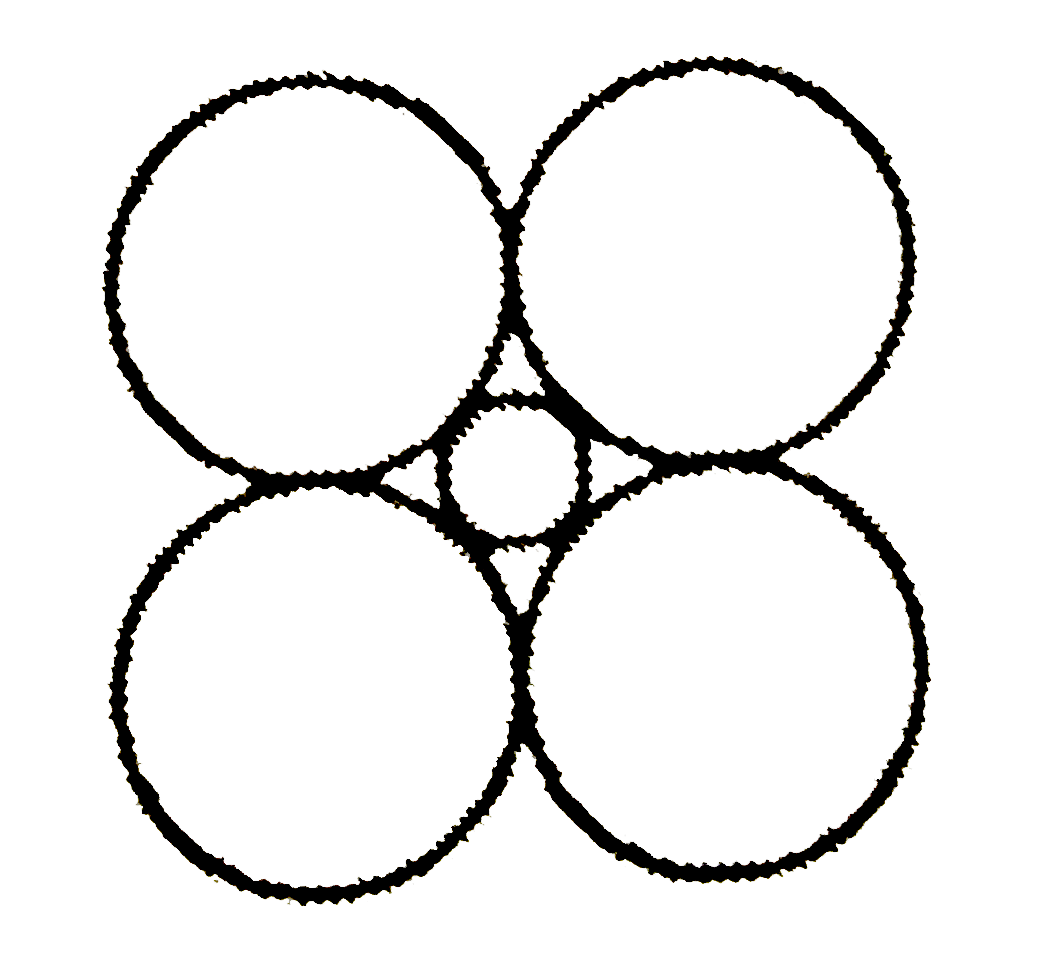 A√2rB(√2−1)rC1√2rD2(√2−1)r
A√2rB(√2−1)rC1√2rD2(√2−1)rThe difference in the areas of two concentric circles is 66 cm2 and the radius of the outer circle is 11 cm. What is the radius of the inner circle?
A8 cmB9 cmC10 cmD7 cm
Out of two concentric circles, the diameter of the outer circle is 26 cm and the chord MN of length 24 cm is tangent to the inner circle. The radius of the inner circle is
View SolutionDraw a semi circle and find the number of lines of symmetry it has.
View SolutionThe instrument used to draw a circle of given radius is ______
View SolutionThe width of a ring is 6 cm and the area of the inner circle is 616cm2 . Find the circumference of the outer circle .
View SolutionThe inner circumference of a circular race track, 14 m wide, is 440 m. Find the radius of the outer circle.
View Solution