Calculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
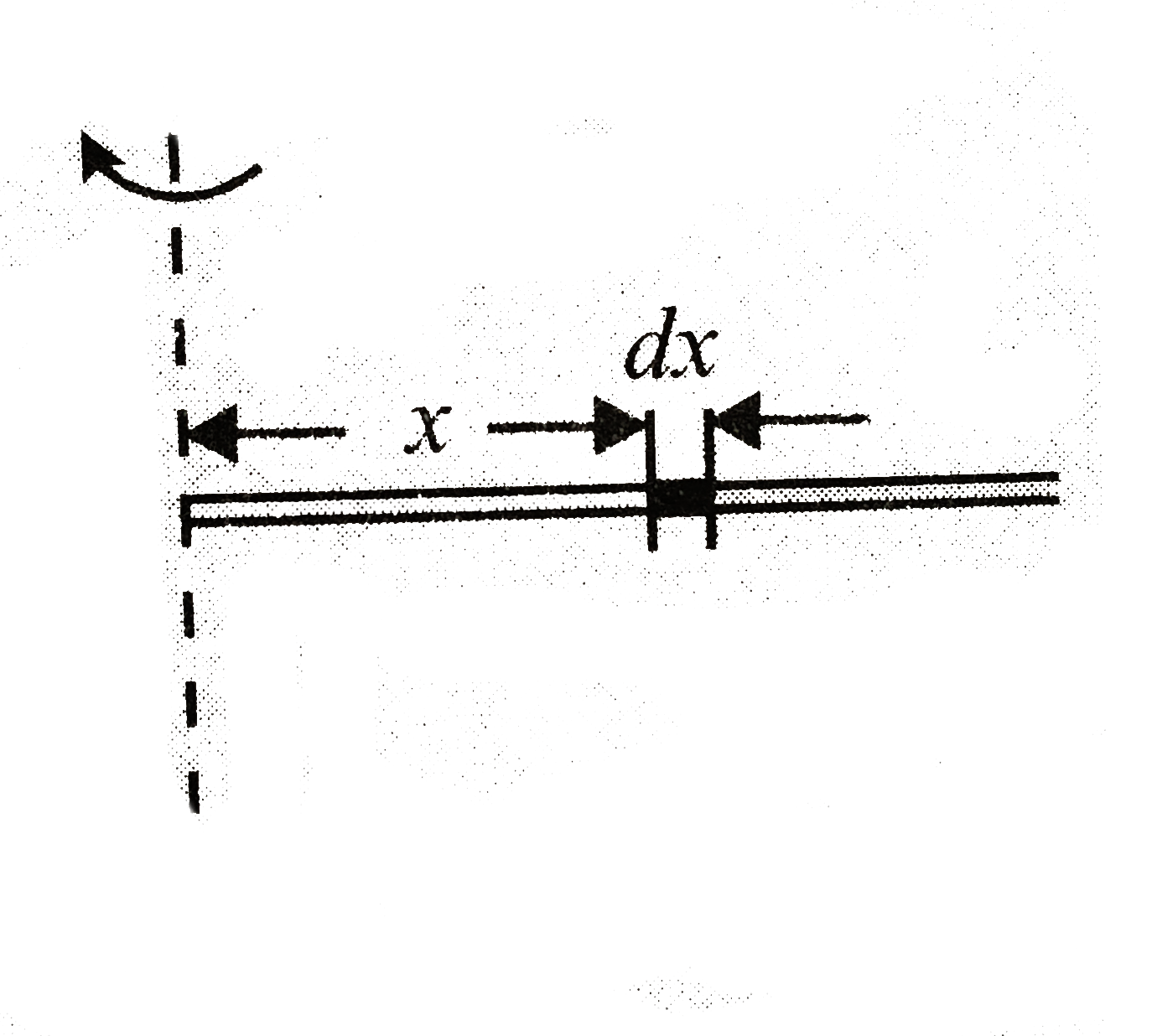
Taking an element of mass dm at a distance x from the relation axis.
I=∫(dm)r2−∫10(Mldx)x2=Ml23
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Calculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View Solution
Knowledge Check
Moment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
Aml212Bml23C7ml248Dml29The M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
AMl2BMl2/3CMl2/2DMl2/12Moment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
AML26BML212C7ML224D7ML248
The moment of inertia of thin rod of linear density λ and length l about an axis passing through one end and perpendicular to its length is
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a uniform rod of length L and mass M , about an axis pasing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a rod of mass 'M', length ? about an axis perpendicular to it through one end is,
View SolutionThe radius of gyration of a uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is
View Solution