A uniform disc of mass m and radius R has an additional rim of mass m as well as four symmetrically placed masses, each of mass m/4 tied at positions R/2 from the centre as shown in Fig. What is the total moment of inertia of the disc about an axis perpendicular to the disc through its centre?

I=Idisc+Iring+Ipoint masses
=mR22+mR2+[m4+(R2)2]=7mR24
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.315videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.411videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionThe mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View Solution
Knowledge Check
- Question 1 - Select One
Two thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is :
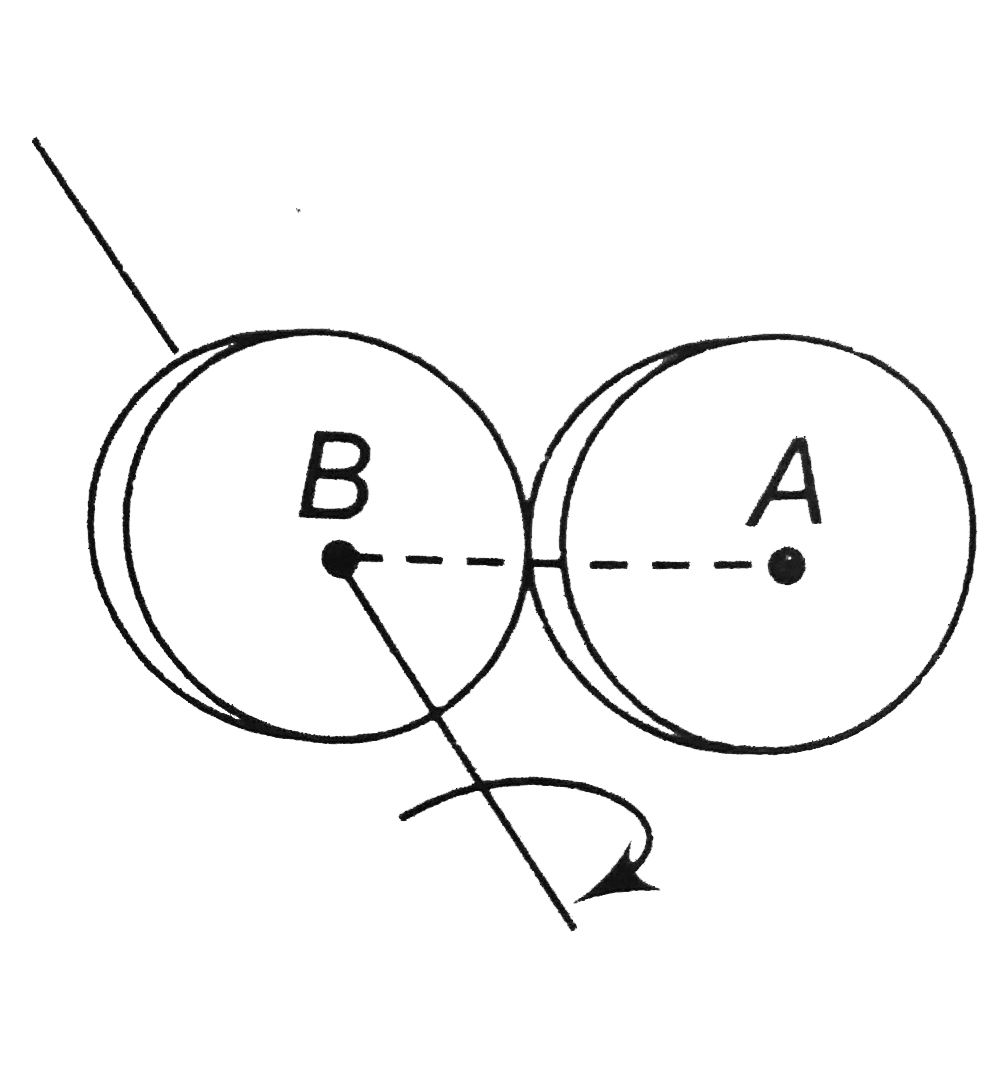 .A2Mr2B3Mr2C4Mr2D5Mr2
.A2Mr2B3Mr2C4Mr2D5Mr2 - Question 2 - Select One
Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
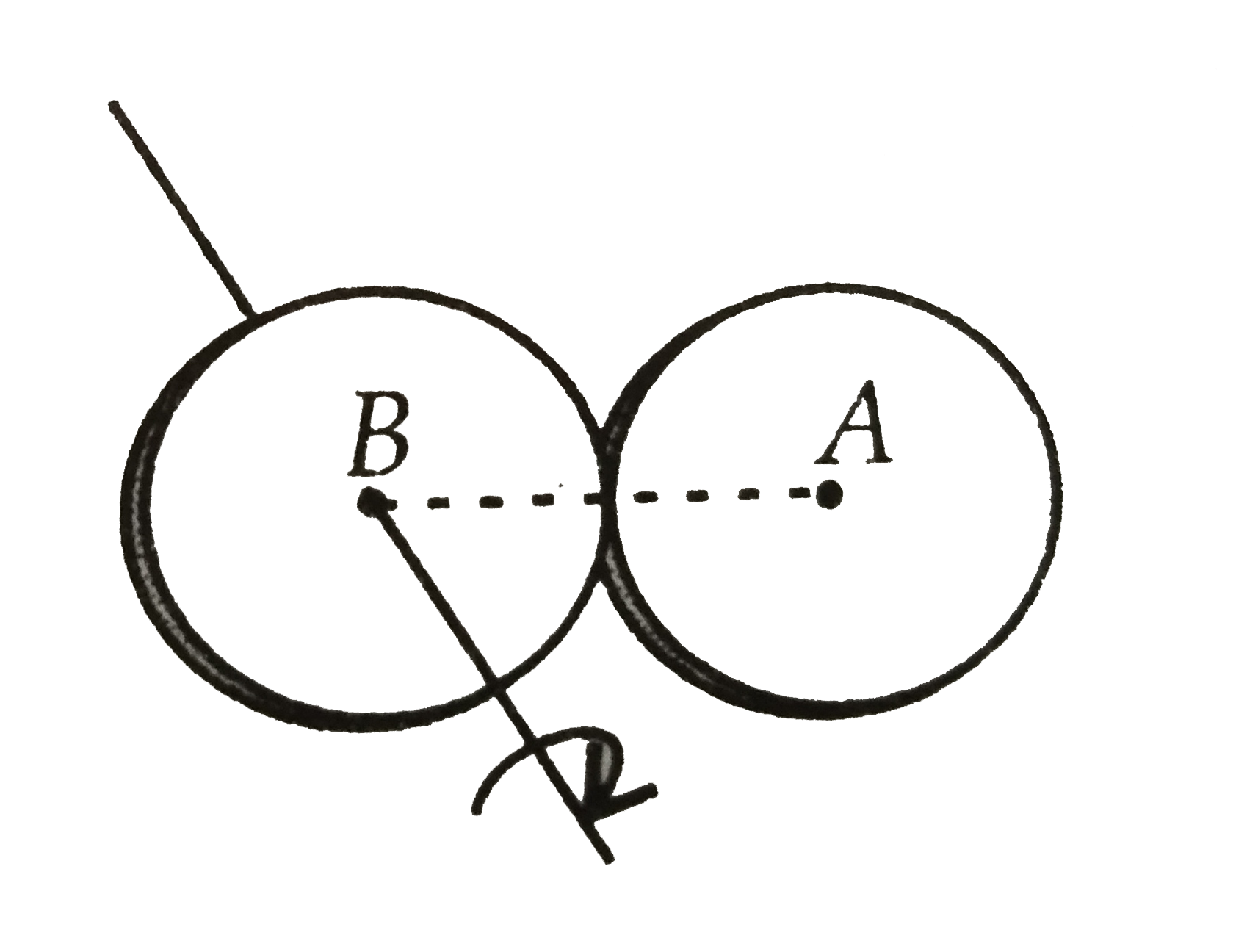 A2Mr2B3Mr2C4Mr2D5Mr2
A2Mr2B3Mr2C4Mr2D5Mr2 - Question 3 - Select One
The moment of inertia of a uniform semicircular disc of mass disc through the centre is
A25Mr2B14Mr2C12Mr2DMr2
Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
View SolutionA thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
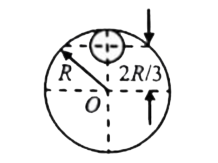 View Solution
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of mass M and radius R3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
View SolutionA semicircular disc of mass M and radius R is free to rotate about its diameter. The moment of inertia of semicircular disc about a line perpendicular to its plane through centre is
View SolutionFrom a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
View Solution

