Find force F required to keep the system in equilibrium. The dimensions of the system are d=0.3m and a=0.2m. Assume the rods to be massless.

150(ˆi)
150(−ˆk)
150(−ˆi)
it cannot be in equilibrium
The correct Answer is:C
Net torque about C is zero
Fa+100x=0
F=−100da=−150
→F=−150ˆi
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Knowledge Check
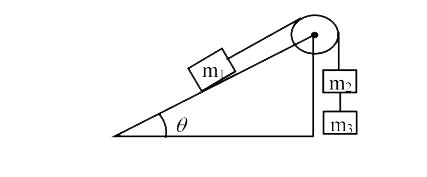
If system is in equilibrium then find relation between m1 and m2
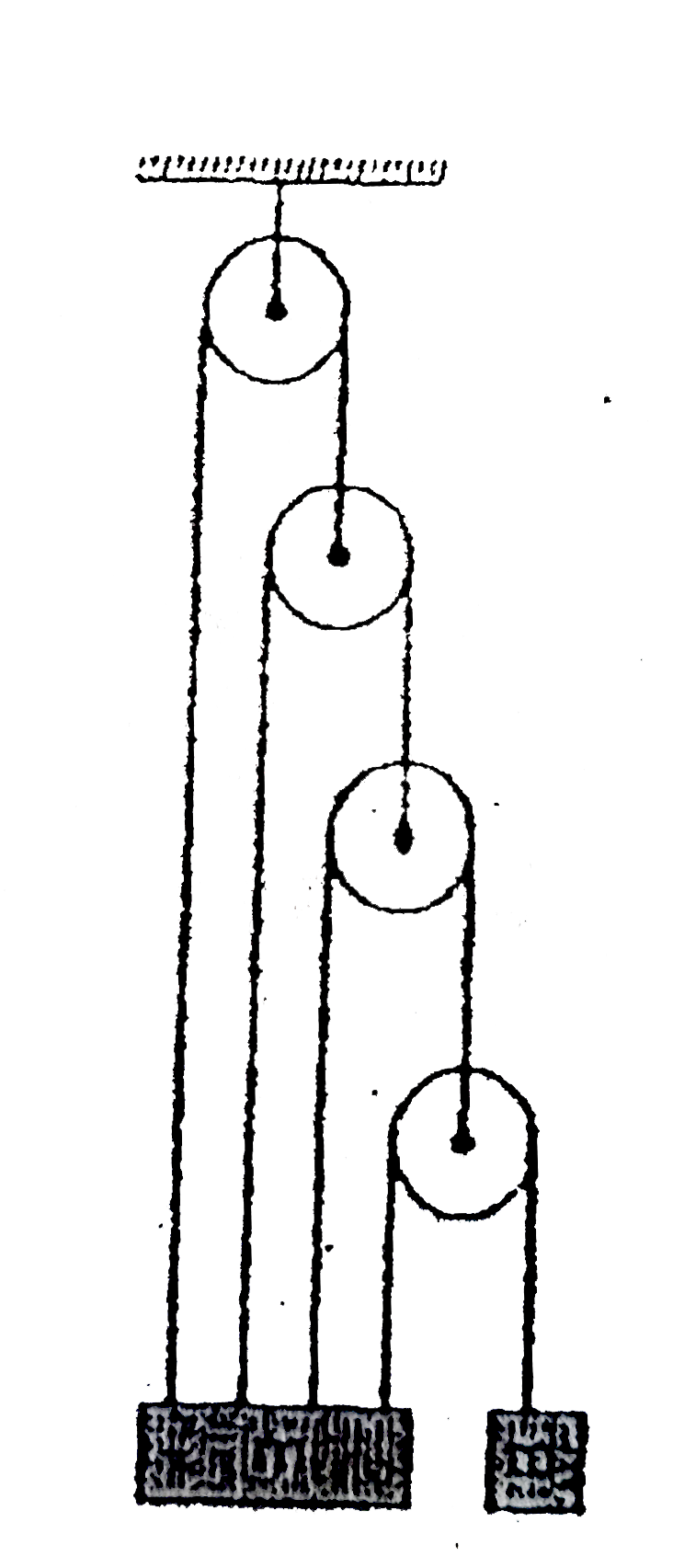 Am1m2=12Bm1m2=115Cm1m2=110Dm1m2=1
Am1m2=12Bm1m2=115Cm1m2=110Dm1m2=1For equilibrium of the system, value of mass m should be
 A9 kgB15 kgC21 kgD1 kg
A9 kgB15 kgC21 kgD1 kg
For the equilibrium of the system shown, the value of mass m should be

View SolutionMasses m1,m2,m3 and m4 are arranged in a system as shown in fig where m1+m2>m3+m4 The lower string keeping the system in equilibrium is burnt The masses start moving. Find the acceleration of masses if the threads are weightless and inextensible the springs are also weightless and the mass of the pulley is negligible.

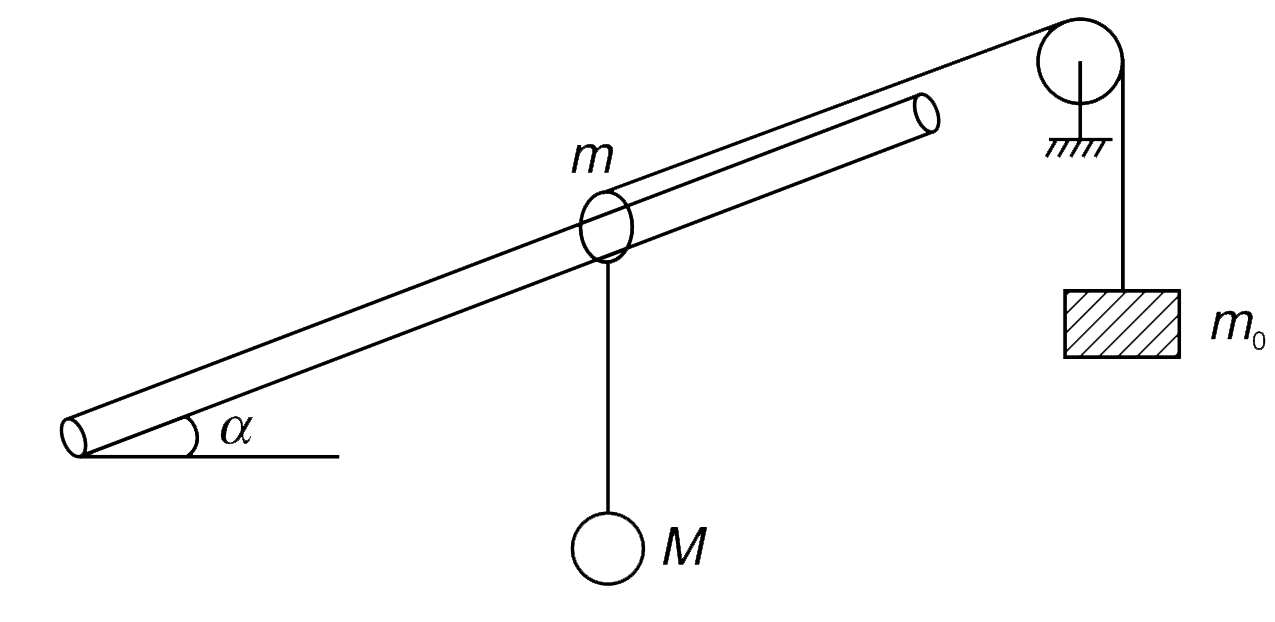
View SolutionA smooth rod is fixed at an angle α to the horizontal. A small ring of mass m can slide along the rod. A thread carrying a small sphere of mass M is attached to the ring. To keep the system in equilibrium, another thread is attached to the ring which carries a load of mass m0at its end (see figure). The thread runs parallel to the rod between the ring and the pulley. All threads and pulley are massless.
(a) Find m0 so that system is in equilibrium.
(b) Find acceleration of the sphere M immediately after the thread supporting m0 is cut.
View SolutionFind the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
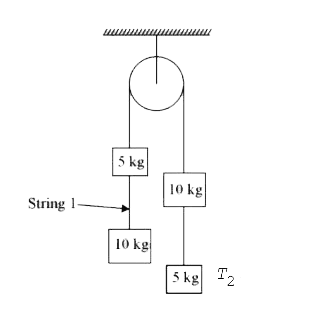
View SolutionFind the value of tension in string 1 if the system equilibrium ? (g=10 m/s2)
View SolutionThe situation shown in the figure, all surfaces are smooth. The mass of sphere is 7 kg if the force F required to keep the system in equilibrium is 9 n N. Then find the value of n.
View Solution