A sphere A moving with speed u and rotating With angular velocity ω makes a head-on elastic collision with an identical stationary sphere B. There is no friction between the surfaces of A and B. Choose the conrrect alternative(s). Disregard gravity.
A will stop moving but continue to rotate with an angular velocity ω
A will come to rest and stop rotating
B will move with speed u without rotating
B will move with speed u and rotate with an angular velocity ω
The correct Answer is:A, C, D
There will be exchange of linear velocities only. However the two spheres cannot exert torques on each other, as their surfaces are firctionless and the angular velocities of the spheres do not change.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m.

What is the net angular impulse about centre of mass imparted to second sphere by the external forces?
View SolutionIf a sphere of mass m moving with velocity u collides with another identical sphere at rest on a frictionless surface, then which of the following is correct ?
View Solution
Knowledge Check
A sphere A moving with a speed u and rotating with an angular velocity ω, makes a head-on elastic collision with an identical stationary sphere B. There is no friction between the surfaces of a and B. Disregard gravity.
AA will stop moving but continue to rotate with an angular velocity ωBA will come to rest and stop rotatingCB will move with a speed u without rotatingDB will move with a speed u and rotate with an angular velocity ωParticle A makes a head on elastic collision with another stationary particle B. They fly apart in opposite directions with equal speeds. The mass ratio will be
A13B12C14D23A solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
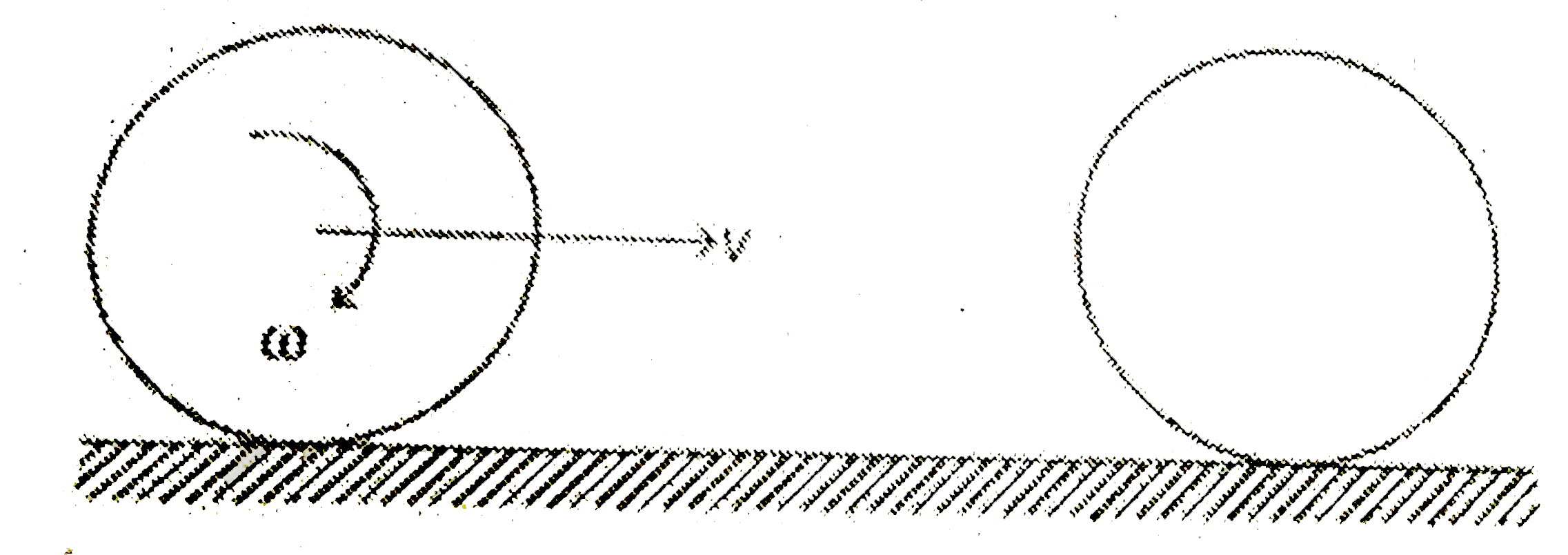
What is the net angular impulse imparted to second sphere by the external forces?A27mRvB57mRvC25mRvD710mRv
A solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m.

Linear velocity of first sphere after it again starts rolling without slipping is:
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
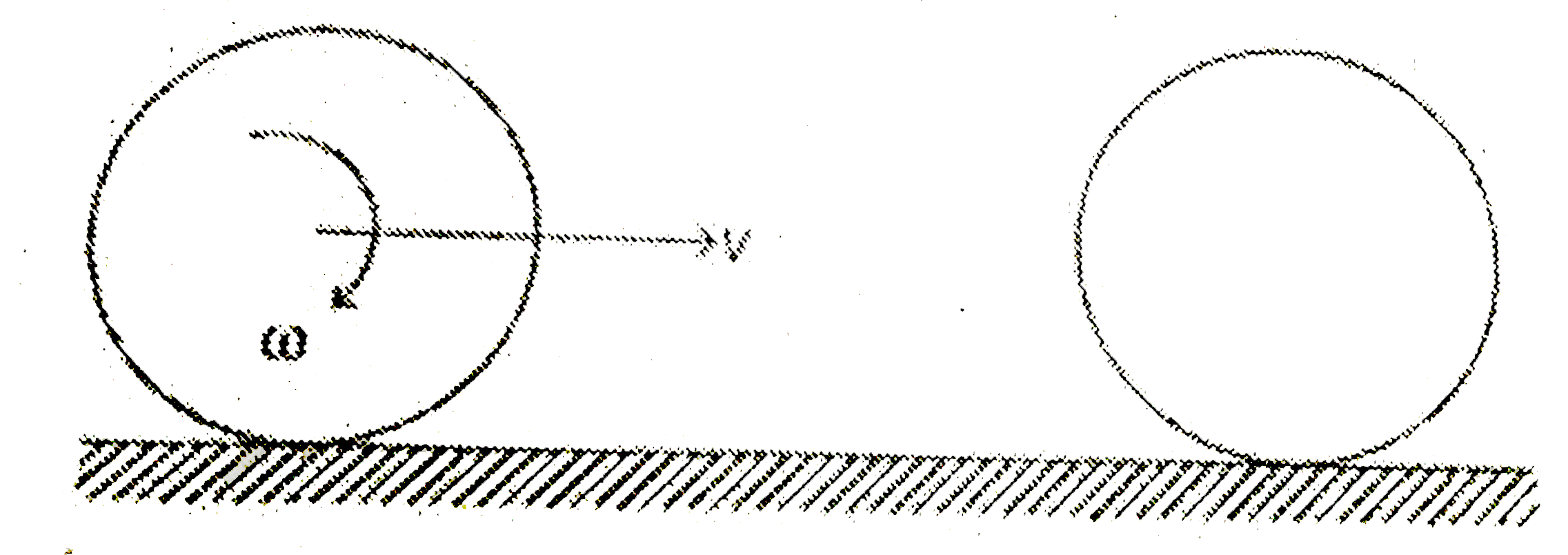
Linear velocity of first sphere after it again starts rolling without slipping is
View SolutionA sphere is moving on a smooth surface with angular velocity ω and linear velocity v. If collides elastically with another identical sphere B kept at rest. Neglecting friction everywhere, let VA and ωA be linear and angular velocities of sphere A after the impact and let VB and ωB be the corresponding parameters for spehre B. Then
View SolutionA sphere has a elastic obique collision with another identical sphere which is initially at rest. The angle between their velocities after the collision is
View SolutionA sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
View Solution
