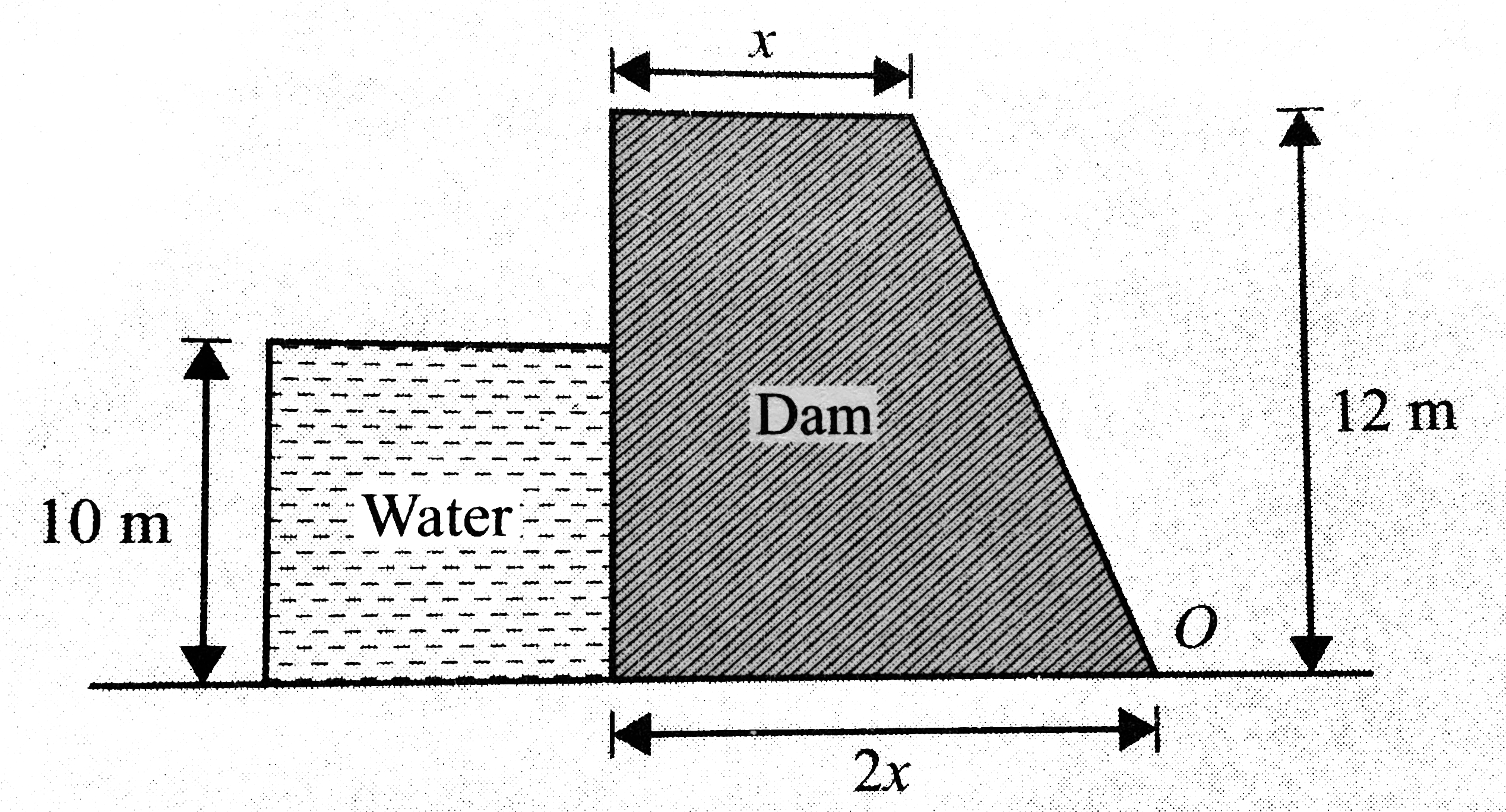
Figure shows a cross sectional view of a masonry dam whose length perpendiclar to te diagram is . The depth of the water behind te dam is . the masonry of which is the dam is constructed has a density of .
a. Find the dimensions and if the weight of the dam is to be times the horizontal force exerted on it by water.
b. Check the stability of the dam with respect to its overturning about the edge through point .
Video Solution
Text Solution
a. Weight of dam volume density
Horizontal thrust due of water (on a vertical surface)
pressure atArea
According to the problem
and
b. Let be the centre of gravity of dam. Taking as origin and the origin and the horizontal axis towards left hand side of as -axis, let r be the distance of centre of gravity from
Anticlockwise torque exerted by the weight of the dam is
clockwise torque due to liquid thrust
As the torque due to the liquid thrust is much less than that due to the weight of the dam, the dam is stable.
|
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Knowledge Check
What is the height of Tehri Dam?
A280.5 mB260.5 mC270.5 mD250.5 mOn which river Omkareswar dam is located ?
ATaptiBRaviCGangaDNarmadaOn which river is the Hirakund Dam situated?
ASutlejBKaveriCMahanadiDBhagirathi

