Find the net downward thrust on the clined surface of a bucket full of water of height h and radii a and b.
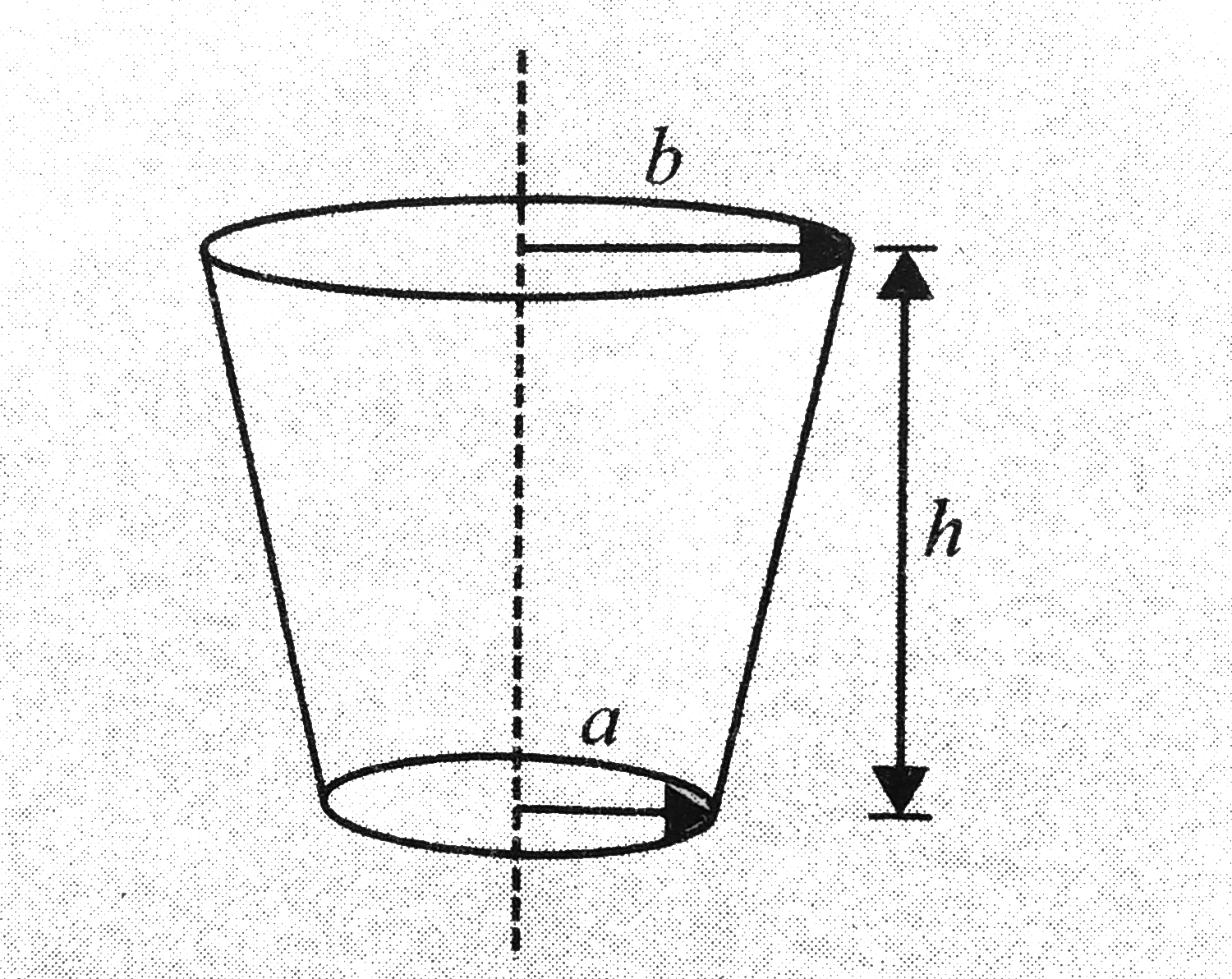
Consider an element of height dx at depth x below the surface

Area =2πr(AB)=2πrdxcosθ
AD≈BC=2r=2[b−(b−ah)x]
Downward thrust is
F=∫dFsinθ=∫h0(xρg)2πrcosθdxsinθdF
=2πtanθ[bh22−(b−ah)h33]
=2πρh(b+2a6)(b−a)
Method 2:
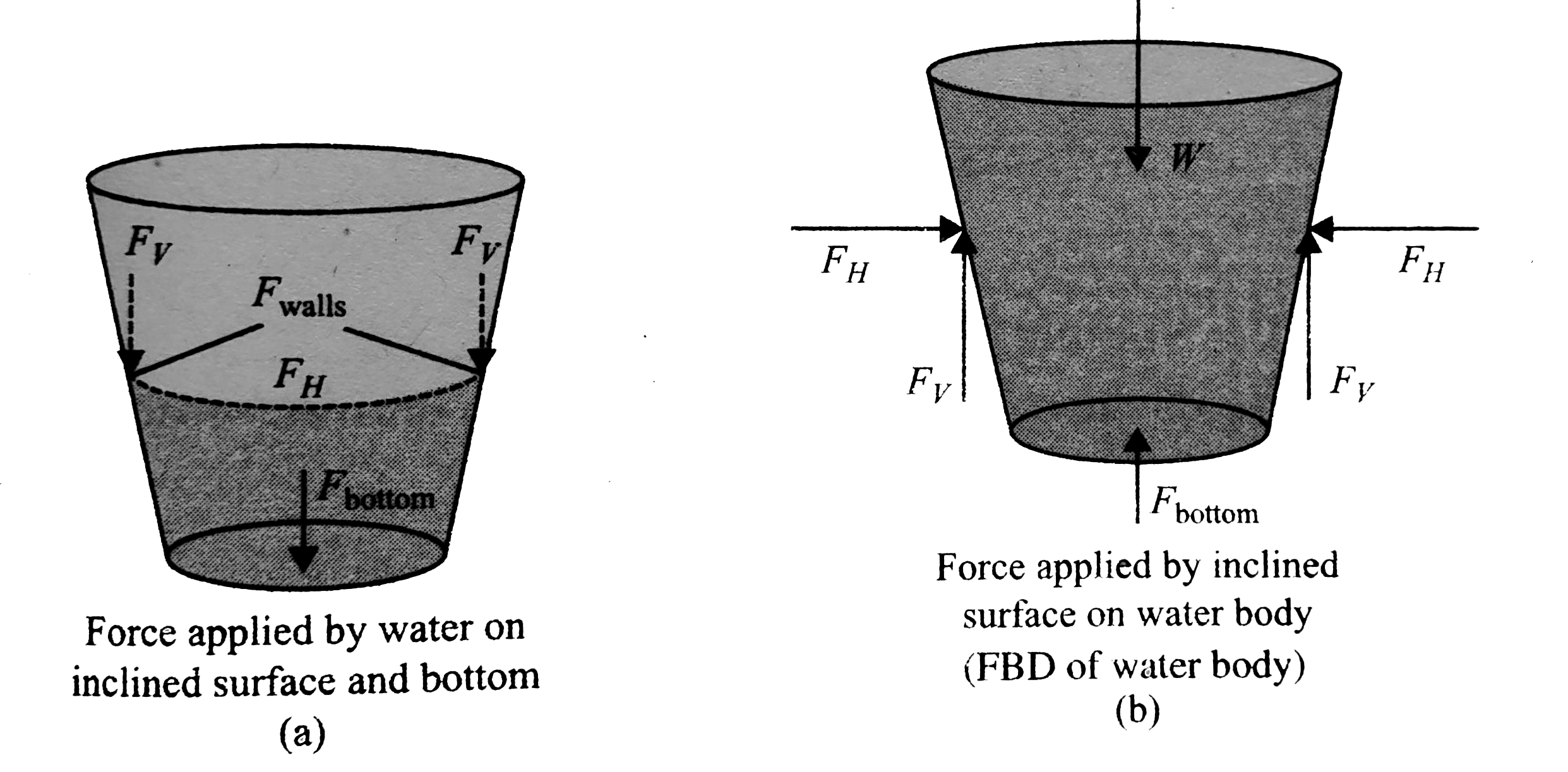
the water will apply normal force on the inclined wall and at the bottom of the container as shown in figure. Force at the bottom of the container is
Fbottom= Pressure at bottom× Area
=(ρgh)(πa2)
=ρghπa2.........i
Weight of water in container is
W=13πh(a2+ab+b2)ρg..........ii
From the free body diagram of the water body
W=Fv+Fbottom
Fv=W−Fbottom
=13πh(a2+ab+b2)ρg−ρghπa2
=13hρg[a2+ab+b2−3a]
=13πρg[ab+b2−2a2]
=13πρgh(b+2a)(b−a)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples7videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.111videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
A man pulls a bucket of water from a depth of h from a well. If the mass of the rope and that of bucket full of water are m and M respectively, the work done by the man is :
A(M+m)ghB(M+m2)ghC(M+m2)ghD(M2+m)gh - Question 2 - Select One
A person pulls a bucket of water from a well of depth h. if the mass of uniform rope is and that of the bucket full 0f water is M, then work done by the person is.
A(M+m2)ghB1/2 (M + m)ghC(M+m)ghD(M2+m)gh
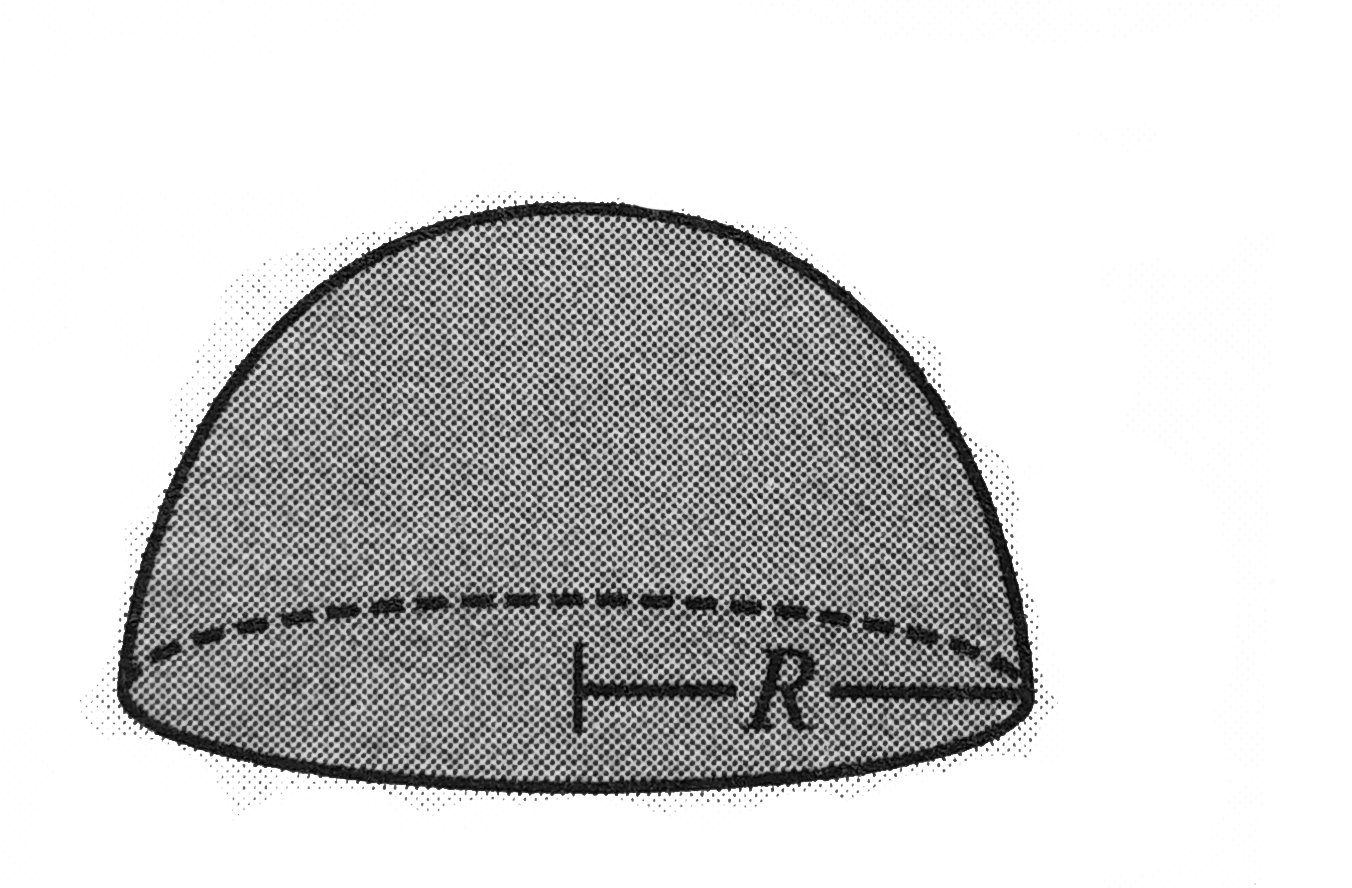
A solid hemisphere of radius R is made to just sink in a liquid of density ρ. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.
 View Solution
View SolutionTrenton is pulling a bucket full of water, out of a well.
What is Trenton working against?View SolutionExplain why the water doesn’t fall even at the top of the circle when the bucket full of water is upside down rotating in a vertical circle ?
View SolutionIf you dip your open palm in a bucket full of water, you feel your hand being pushed up. Why?
View SolutionA cylinder bucket of diameter 28 cm and height 20 cm was full of sand. When the sand in the bucket was poured on the ground, the sand got converted into a shape of a cone. If the height of the cone was 14 cm , what was the base area of the cone?
View SolutionA bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are are 28 and 21 cm respectively. Find the height of the bucket.
View Solution

