A large block of ice $5 m$ thick has a vertical hole drilled through it and is floating in the middle of a lake. What is the minimum length of a rope required to scoop up a bucket full of water through the hole? Relative density of ice $= 0.9$ .

Video Solution

Text Solution

Verified by Experts

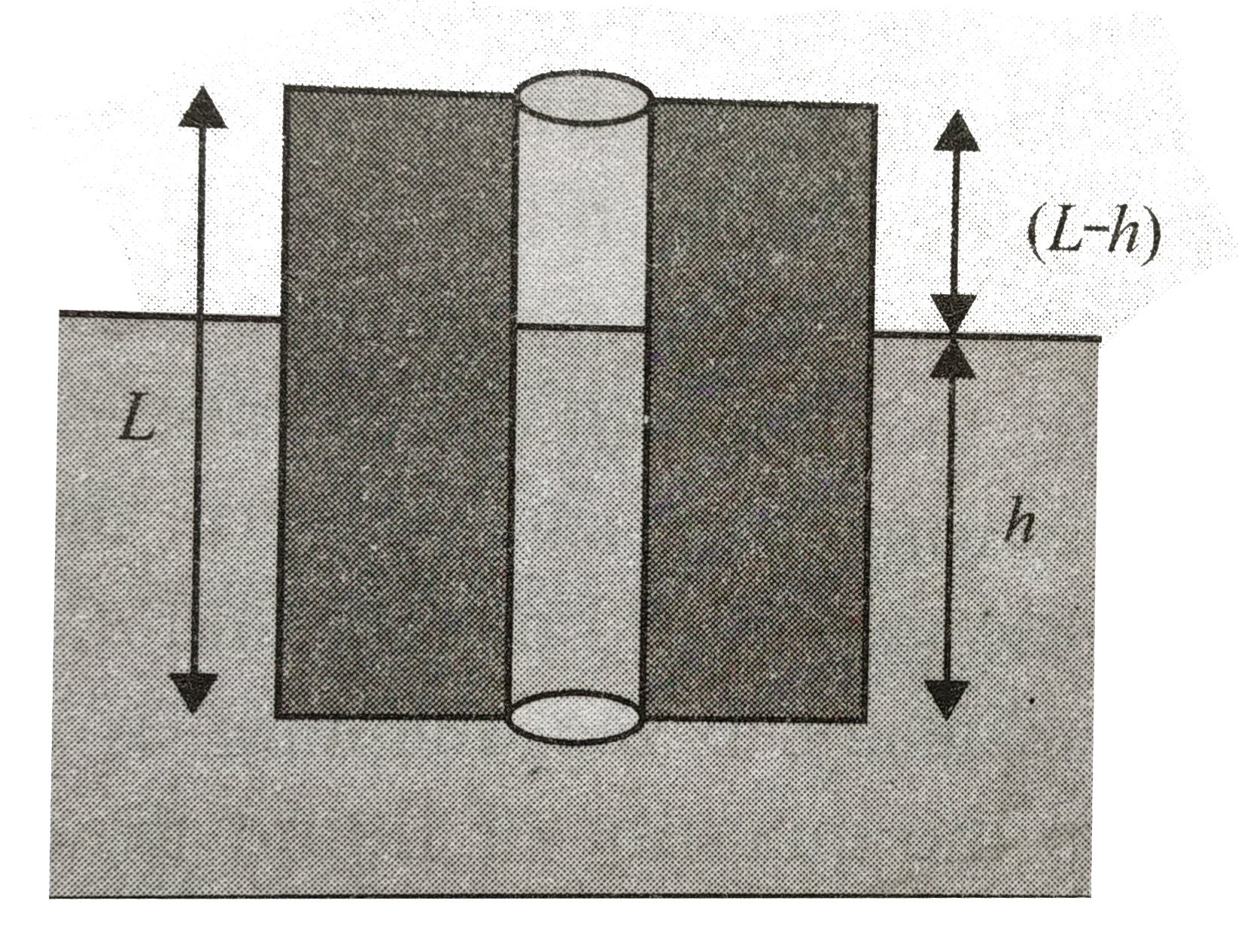
As ice is floating, $W = T h$ , ice $V ρ g = V_{\in} σ_{W}$ . Now if $A$ is the cross section of the block , $L$ its thickness and out of $L, h$ is inside water, $V = A L$ and $V_{\in} = A h$

$A l ρ_{ice} = h A ρ_{water}$
$h = \frac{ρ_{ice}}{ρ_{water}} L K = 0.9 \times 5 = 4.5 m$
i.e., $4.5 m$ of ice will be submerged in water. So the level of water in the hole will be $5 - 4.5 = 0.5 m$ below the top of ice and hence the length of rope required to scoop up water is $0.5 m$ .

Updated on:21/07/2023

A large block of ice 4 m thick has a vertical hole drilled through it and is floating in the middle of water in a lake. The minimum length of rope required to scoop up a bucket full of the through the hole is (density of ice $= 0.9 C G S$ unit, density of water $= 1 C G S$ unit)
A40 cm
B24 cm
C20 cm
D360 cm
A large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum of water through the hole is (density of ice $= 0.9 g c m^{- 3})$
A0.5 m
B1.0 m
C1.2 m
D1.8 m
The thickness of the ice layer on the surface of lake is 20 m. A hole is made in the ice layer. What is the minimum length of the rope required to take a bucket full of water out ? (Take density of ice $= 0.9 \times 10^{3} k g / m^{3})$
A2 m
B5 m
C9 m
D18 m