A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
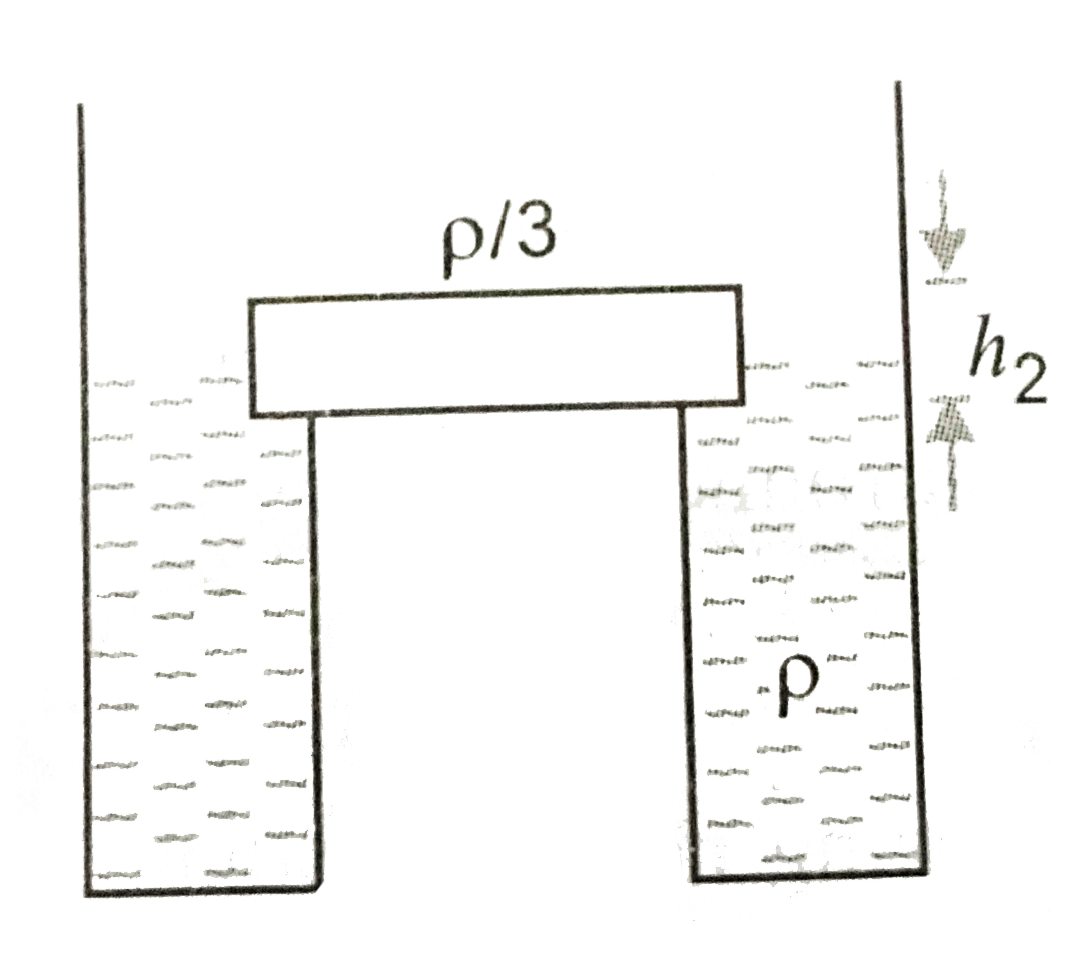
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height h1 (in situation 1), for which the block just starts to move up?
2h/3
5h/3
5h/3
5h/2
The correct Answer is:C
Consider the eqilibrium of wooden block. Forces acting in the downward direction are as follows
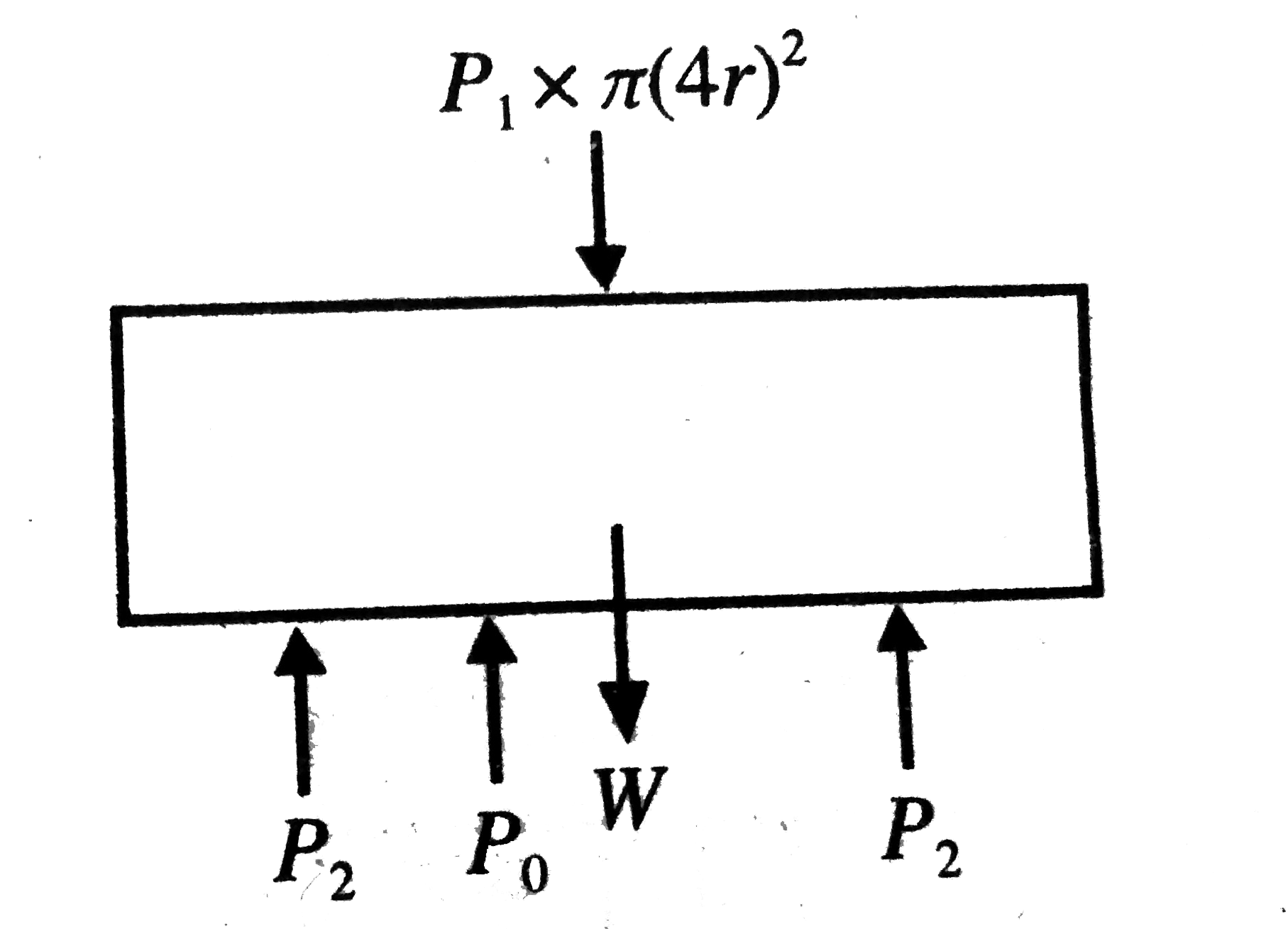
a. Weight of wooden cylinder
=π(4r)2×h×ρ3×g=π×16r2hρ3g
b. Force due to pressure (P1) created by liquid of height h1 above the wooden block is
=P1×π(4r2)=[P0+h1ρg]×π(4r2)
=[ρ0+h1ρg]π×16r2
Force acting on the upward direction due to pressure p0 exerted from below wooden block and atmospheric pressure is
=p2×π[(4r)2−(2r)2]+P0×(2r)2
[ρ0+h1ρg]π×16r2
Force acting on the upward directioin due to pressure P0 exerted from below the wooden block and atmpsheric pressure is
=p2×π[(4r)2−(2r)2]+P0×(2r)2
=[P0+(h1+h)ρg]×π×12r2+4r2P0
At the verge of rising
[P0+(h1+h)ρg]π×12r2+4r2P0
π×10r2h×ρ3g+[P0+h1ρg)×π×16r2
12h1+12h=16h3+16h
12h1−16h3=4h1⇒5h3h1
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - MCQ_TYPE
3 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.
View SolutionA wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

The block in the above question is maintained by external means and the level of liquid is lowered. The height h2 when this external force reduces to zero is
View Solution
Knowledge Check
A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if h2 is further decreased, thenA(a) cylinder will not move up and remains at its original positionB(b) for h2=h3, cylinder again starts moving upC(c) for h2=h4, cylinder again starts moving upD(d) for h2=h5, cylinder again starts moving upA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceA(a) h3B(b) 4h9C(c) 2h3D(d) hA wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If height h2 of water level is further decreased, thenAcylinder will not move up and remains at its original positionBfor h2=H/3 , cylinder again starts moving upCfor h2=H/4 , cylinder again starts moving upDfor h2=H/5 , cylinder again starts moving up
A wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If level of liquid starts decreasing slowly, when the level of liquid is at a height h1 above the cylinder, the block just start moving up. Then the value of h1 is
View SolutionA wooden cylindrical of diameter 4r, height h and density ρ/3 is kept on a hole of diameter 2r of a tank , filled with water of density ρ as shown in the figure . The height of the base of cylinder from the base of tank is H .
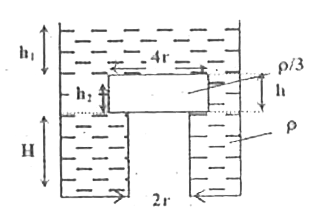
Let the cylinder is prevented from moving up , by applying a force and water level is further decreased . Then , height of water level (h2 in figure ) for which the cylinder remains in original position without application of force is
View SolutionA block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View SolutionAn open pan P filled with water (density ρm) is placed on one side of the pan as shown. If water depth is more then height of the block, then choose the correct statement.
View Solution
