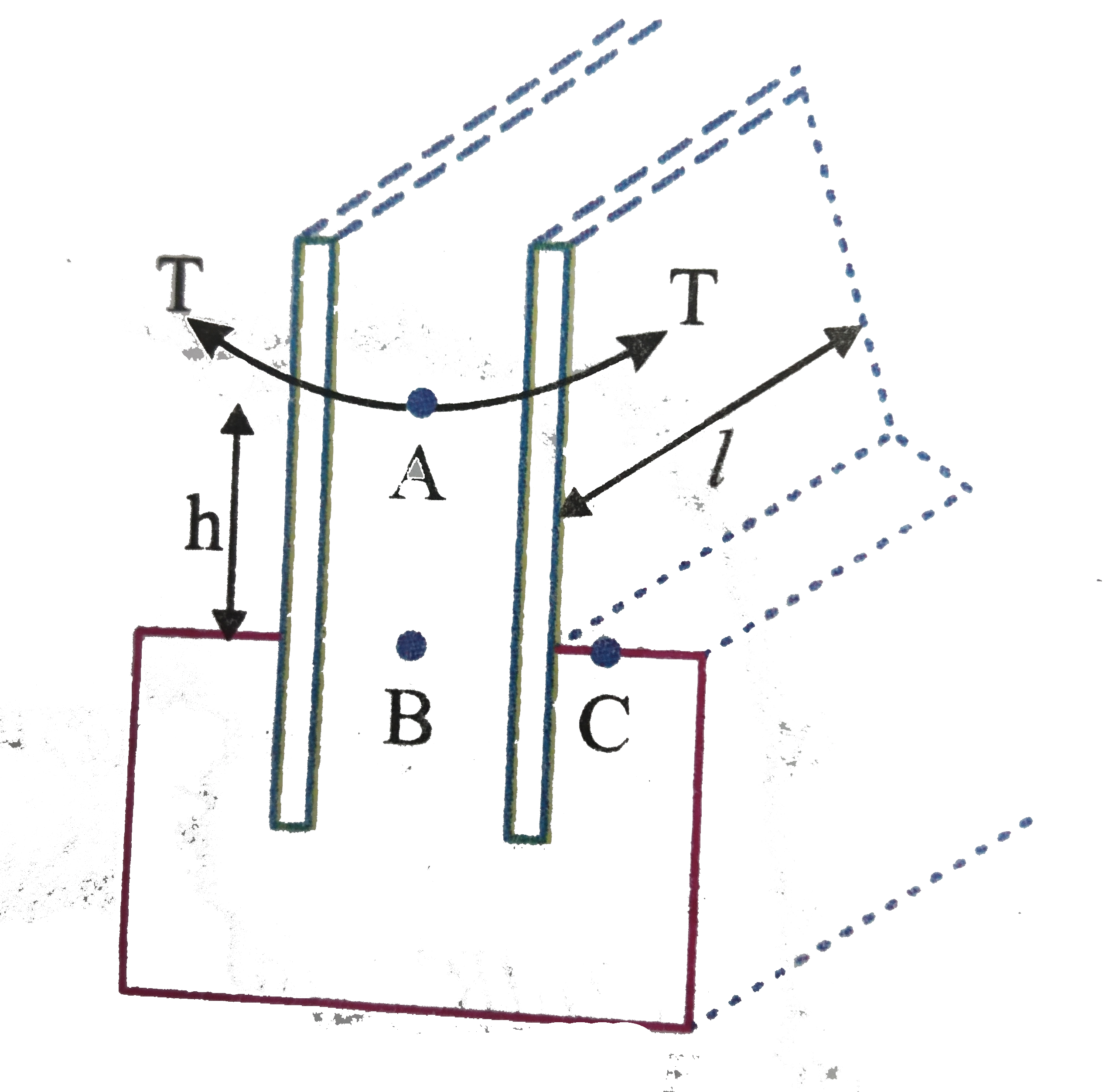
Derive an expression for the height of capillary rise between two parrallel plates dipping in a liquid of density $σ$ separated by a distance $d$ . The surface tension of the liquid is $T$ .

Video Solution

Text Solution

Verified by Experts

The menisus between two plates is cylindrical in shape. Pressure at $A$ (the lowest point of the menisus)
$p_{A} = p_{0} = T . r$
Pressure at $B =$ pressure at $C = p_{0} =$ pressure at $A + ρ g h$
$∴ p_{0} = p_{0} - \frac{T}{r} + ρ g h \times h = \frac{T}{ρ g r} - \frac{2 T}{ρ g d}$
Alternative method:
Force upward $= 2 l T cos θ = 2 l T$ ( $∵ θ = 0^{\circ})$
Gravitational pull $= (Volume \times Density) g = l h d ρ g$
$∴ 2 l T = I h d ρ g \Rightarrow h = \frac{2 T}{d}$

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

Expression for the height of capillary rise between two parallel plates dipping liquid of density $σ$ separated by a distance d. The surface tension of the liquid is T. [Take angle of contact to be zero]
A $h = \frac{2 T}{σ d g}$
B $h = \frac{2 d}{σ T}$
C $h = \frac{σ T}{d}$
D $h = \frac{2 T^{2}}{σ d}$
Question 2 - Select One
The height of liquid column in capillary tube is h the radius of capillary tube is r. $ρ$ is the density of liquid , g is acceleration due to gravity and $θ$ is angle of contact . The surface tension of the liquid is ,
A $t = \frac{r h ρ g}{2 cos θ}$
B $T = \frac{2 cos θ}{h ρ g} r$
C $T = \frac{2 cos θ}{r ρ h g}$
Dall of these
Question 3 - Select One
What is the height to which a liquid rises between two long parallel plates, a distance d apart ? (Surface tension of liquid is T and density is $ρ$ )
A $\frac{4 T}{ρ g d}$
B $\frac{2 T}{ρ g d}$
C $\frac{T}{ρ g d}$
D $\frac{T}{2 ρ g d}$

CENGAGE PHYSICS-PROPERTIES OF SOLIDS AND FLUIDS-INTEGER_TYPE

Home
Ask Doubt
Profile