On gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress ∝ strain or, Stressstrain = a constant for the material of wire.
Two wires of same material have length and radius (L,r) and (2L,r2). The ratio of their young's moduli is

1:2
2:3
2:1
1:1
The correct Answer is:D
Young's modulus is a material constant. So length and radius do not effect its value. So ratio has to be 1:1.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Integer6videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Fill In The Blanks1videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Assertion- Reasoning13videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
Similar Questions
Knowledge Check
- Question 1 - Select One
On gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress prop strain or, Stressstrain = a constant for the material of wire.
Just on crossing the yield region, the material will have Aincreased and breaking stressBreduced and breaking stressCconstant stressDNone of these
Aincreased and breaking stressBreduced and breaking stressCconstant stressDNone of these - Question 2 - Select One
Two wires of same material and length have the radii of their cross sections as r and 2r, respectively. The ratio of their resistances
A2:1B4:1C1:4D3:2 - Question 3 - Select One
Two wires of same material and length have the radii of their cross sections as r and 2r, respectively. The ratio of their resistances
A2:1B4:1C1:4D3:2
The ratio of radii of two wires of same material is 2:1. If they are stretched by the same force, the ratio of their stress is
View SolutionThe young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
View SolutionTwo wires of same diameter of the same material having the length l and 2l If the force F is applied on each, the ratio of the work done in two wires will be
View SolutionIf breaking stress of a wire of length L and radius of cross-section r is P N/m2, then breaking stress of wire of same material of length 2 L and radius of cross section (r/2) will be
View SolutionFind the ratio of stress present in wire-1 to the wire-2 shown in the diagram while both wires have same material & friction.
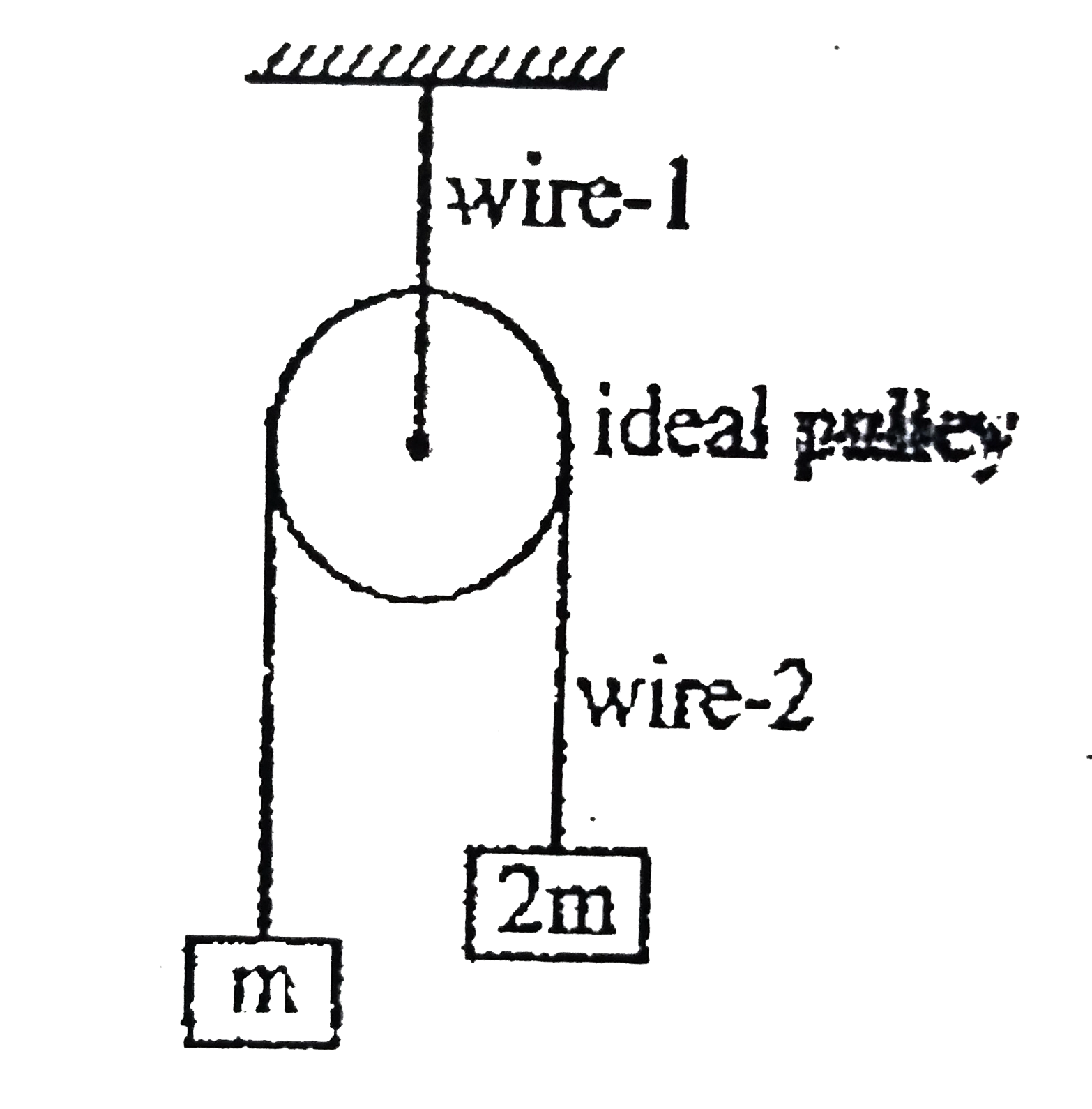 View Solution
View Solution

