Given that T2=kR3, express the constant k of the above relation in days and kilometres. Given, k=10−13s2m3. The Moon is at a distance of 3.84×105km from the earth. Obtain its time period of revolution in days.
Given k=10−13s2m−3
=10−13[1(24×60×60)2d2][1(1/1000)3km3]
=1.33×10−14d2km−3
T2=KR3 or T=(KR3)12
∴T=[1.33×10−14×(3.84×105)3]1/2=27.3d
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Exercise 6.2
15 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Exercise 6.3
16 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Given that T2=kR3, express the constant k of the above relation in days and kilometres. Given, k=10−13s2m−3. The Moon is at a distance of 3.84×105km from the earth. Obtain its time period of revolution in days.
View SolutionA laser beam has a wavelength of 7×10−7m and aperure 10−2m. The beam is sent to moon at a distance of 4×105km from earth. Find the angular spread and areal spread of the beam on reaching the moon.
View Solution
Knowledge Check
An ideal gas expands in volume from 1×103m3 at 300 K against a constant pressure of 1×105 N m−2.The work done is
A−900 JB−900 kJC270 kJD900 kJRate constant of two reactions are given below. Identifying their order of reaction
k=5.3×10−2Lmol−1s−1
k=3.8×10−4s−1A(i) second order, (ii) first orderB(i) first order, second orderC(i) zero order, (ii) first orderD(i) second order, (ii) zero orderIf the mass of earth were 2 times the present mass, the mass of the moon were half the present mass and the moon were revolving round the earth at the same present distance, the time period of revolution of the moon would be (in day)
A56B28C14√2D7
The time taken by the earth to complete one revolution around the sun is 3.156×107s . The distance between the earth and the sun is 1.5×1011 m. Find the speed of revolution of the earth.
View SolutionHow fast (in m2s−1) is area swept out by (a) the radius from sun to earth ? (b) the radius from the sun to earth =1.496×1011m , Distance of earth to moon =3.845×108m and period of revolution of moon =2713 days.
View SolutionThe Earth and Jupiter are two planets of the sun. The orbital radius of the earth is 107m and that of Jupiter is 4×107m If the time period of revolution of earth is T=365 days find time period of revolution of the Jupiter
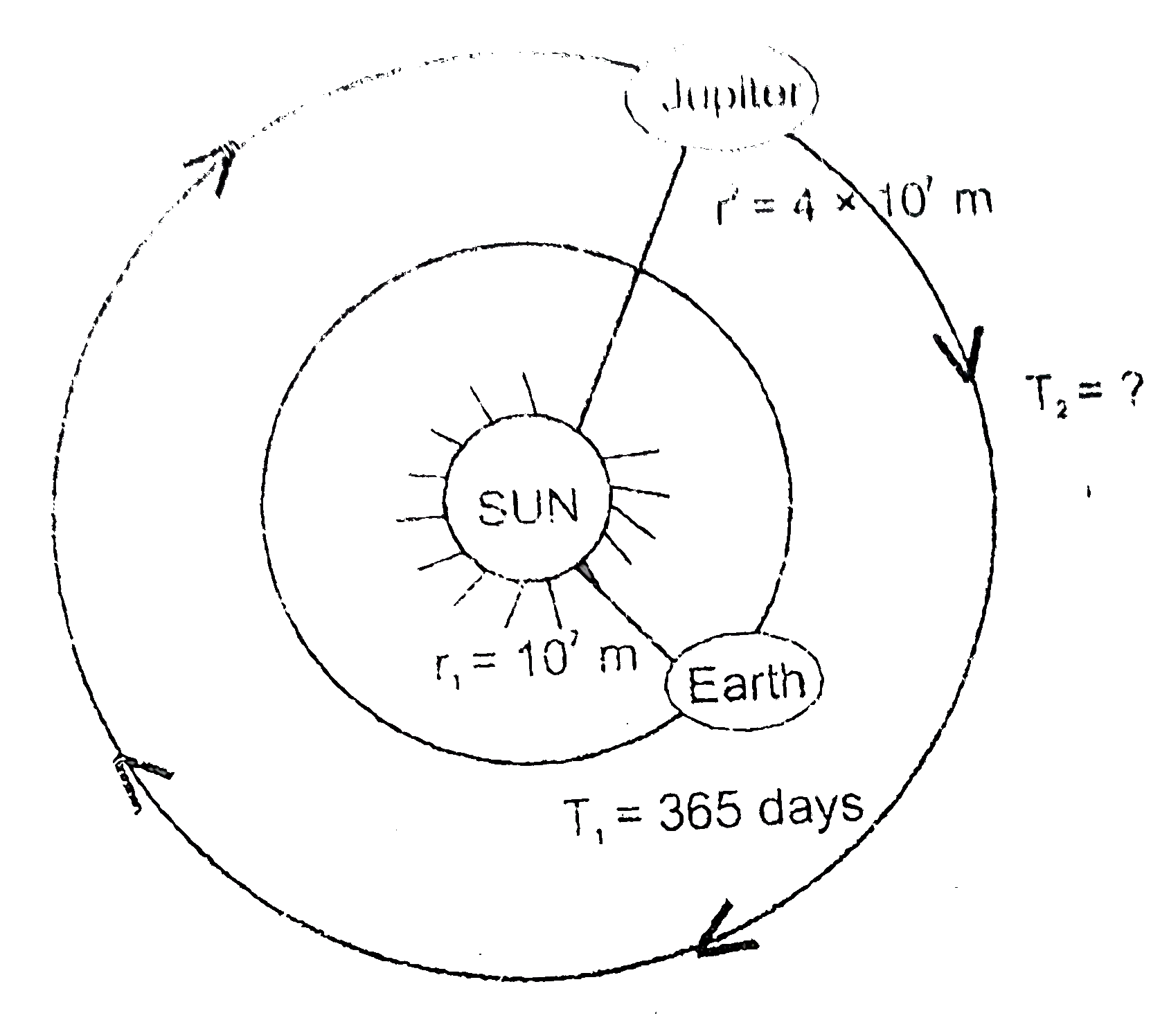 .
.
View SolutionAccording to kepler's law of periods, T2=kr3, where k is a constant. Compute the constant k for (a) the earth and (b) the venus. Given that orbital radii of the earth and the venus are 1.496×1011m and 1.082×1011m, and their respective periods are 1 year and 0.615 year.
View SolutionFind the accelerationof the moonwith respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution aroudn the earth =27.3days
View Solution
