Statement I: The magnitude of the gravitational potential at the surface of solid sphere is less than that of the centre of sphere. Statement II: Due to the solid sphere, the gravitational potential is the same within the sphere.
Statement I is True, Statement II is True: Statement II is a correct explanation for Statement I.
Statement I is True, Statement II is True: Statement II is Not a correct explanation for Statement I.
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:C
Vin=GM2R3[3R2−r2]
Vin=32Vs
Vin>Vs
V is not same everywhere as indicated by Vin.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Linked Comprehension23videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Integer5videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Multiple Correct24videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
Two spheres one of mass M has radius R. Another sphere has mass 4M and radius 2R. The centre to centre distance between them is 12R. Find the distance from the centre of smaller sphere where
(a) net gravitational field is zero,
(b) net gravitational potential is half the potential on the surface of larger sphere.View SolutionGravitational Potential|Gravitational Potential Due To Point Mass|Gravitational Potential Due To Spheres
View Solution
Knowledge Check
- Question 1 - Select One
The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
AGMa2BGMa3CGM2aDzero - Question 2 - Select One or More
Due to a solid sphere, magnitude of
Agravitational potential is maximum at centreBgravitational potential is minimum at centreCfield strength is maximum at centreDfield strength is minimum at centre - Question 3 - Select One
Gravitational field due to a solid sphere
Aremains constant throughout the sphereBincrease inside the sphere and decreases outside the sphereCincreases throughout with distance from the centerDdecreases throughout with distance from the centre
Match the entries given in column I with those given in column II.
Column IColumn II(A)Plot of gravitational field due to a uniform solid sphere with distance from its centre.(p)Continuos(B)Plot of gravitational field due to a thin spherical shell with distance from centre.(q)Discontinuos(C)Plot of gravitational potential due to a uniform solid sphere with distance from centre.(r)Straight line(D)Plot of gravitational potential due to a thin spherical shell with distance from centre.(s)Rectangular hyperbola(t)ParabolaView SolutionGravitational field at the surface of a solid sphere is 1.5×10−4N kg−1. Find the gravitational field at a point situated inside the sphere at a distance equal to half of rhe radius of the solid sphere.
View SolutionThe ratio of the radii of gyration of a hollow sphere and a solid sphere of the same radii about a
View SolutionSTATEMENT-1: The gravitational potential energy of a solid sphere is negative.
STATEMENT-2: Two masses attract each other.View SolutionAssertion: A positively charged rod is held near a neutral conducting solid sphere as illustrated below. The sphere lies on a insulated stand. The potential of ground (or earth) is zero. The potential at point A (point A need not be centre of the sphere) is higher compared to potential of gound (earth).
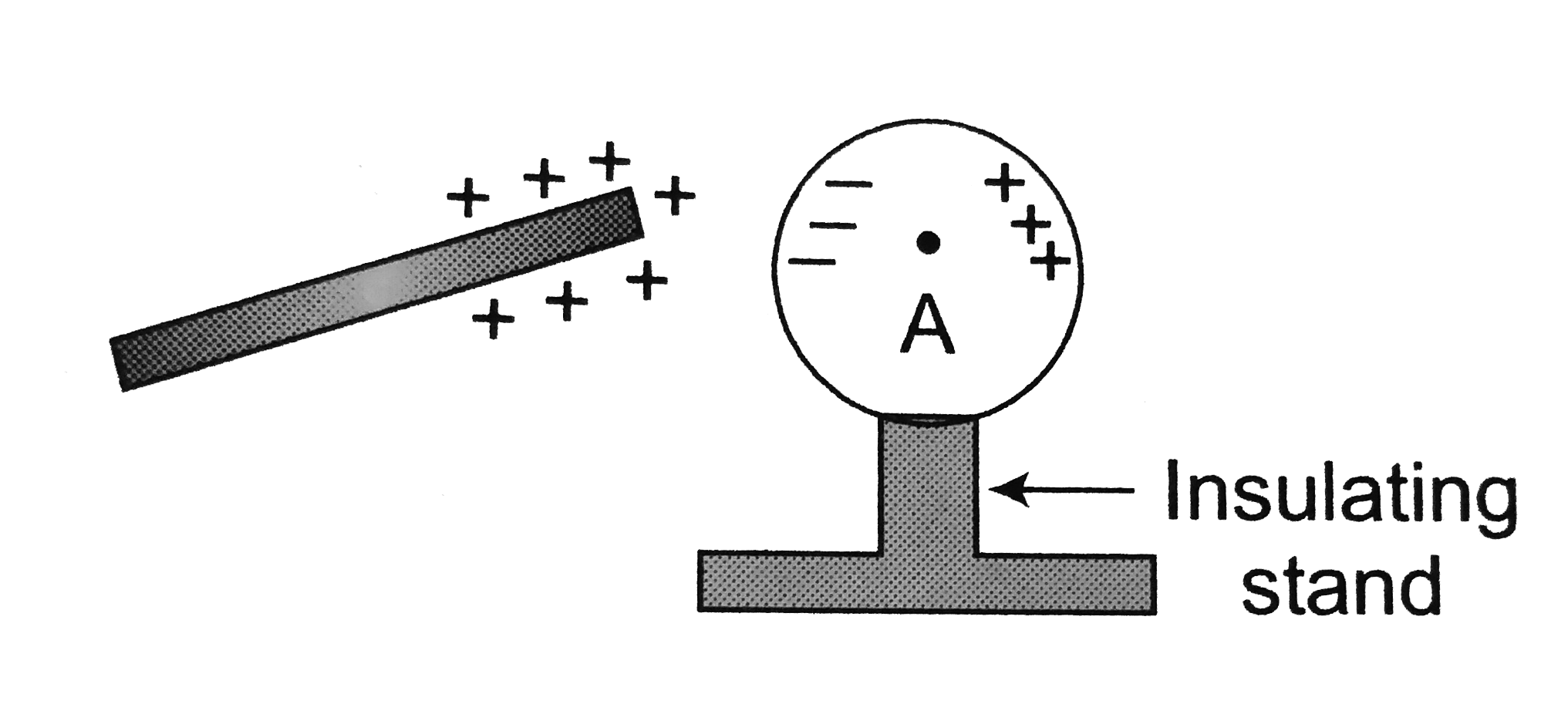
Reason: In this situation of assertion, the potential at the centre of conducting sphere is positive. the solid sphere being conducting, potential at each point in the sphere is same.View Solution

