Obtain on expression for impedance and current in series LCR circuit. Deduce an expression for the resonating frequency of an LCR series reasonating circuit.

Text Solution

Verified by Experts

Circuit consists of resistor of resistance R, inductor of inductance L and capacitor of Let i be the current and q be the charge at any instant t.
Back e.m.f across inductor is $- L \frac{d i}{d t}$
and across capacitor is $\frac{- q}{C}$
Total e.m.f $= V_{m} sin ω t - L \frac{d i}{d t} - \frac{q}{C}$

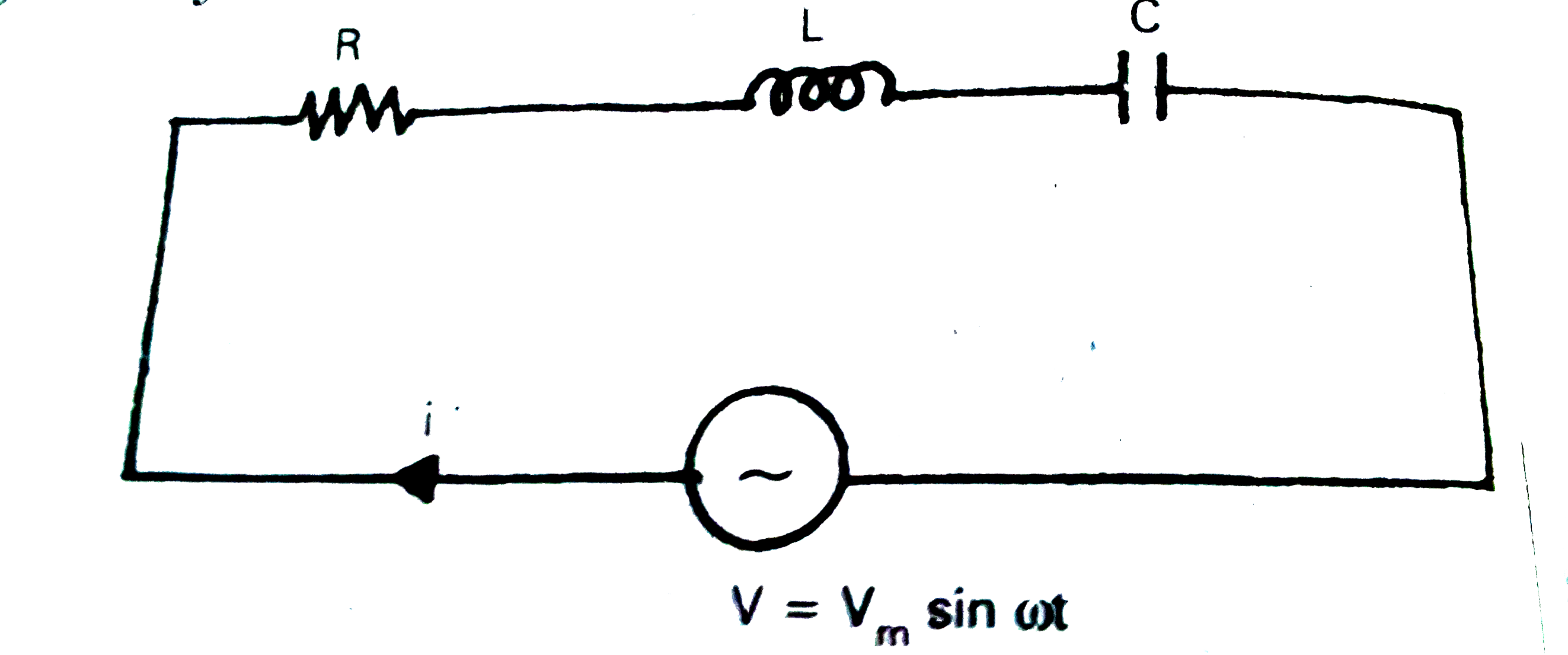
According to Ohms law, this must be equal to iR
$V_{m} sin ω t - L \frac{d i}{d t} - \frac{q}{C} = i R$
$L \frac{d i}{d t} + i R + \frac{q}{C} = V_{m} sin ω t$ .....(1)
The current i any instant in the circuit is
$i = i_{m} sin (ω t - ϕ)$ if $ω L \geq \frac{1}{ω C}$ which is possible at high frequencies.
$i = i_{m} sin (ω t + ϕ)$ if $ω L < \frac{1}{ω C}$ which is possible at low frequencies.
The maximum current $(i_{m})$ is given by
$i_{m} = \frac{V_{m}}{\sqrt{R^{2} + {(\frac{1}{ω c} - ω L)}^{2}}}$ ....(2)
Its impedance $(Z) = \frac{V_{m}}{i_{m}} = \sqrt{R^{2} + {(\frac{1}{ω C} - ω L)}^{2}}$ ....(3)
Let $ϕ$ be the phase difference between current and e.m.f
$ϕ = {tan}^{- 1} ⎛ ⎝ \frac{\frac{1}{ω C} - ω L}{R} ⎞ ⎠$ ....(4)
Resonant freuency $(f_{0})$ :
At this frequency, the impedance of LCR circuit is minimum and is equal to R. At this frequency current is maximum. This frequency is called resonant frequency $(f_{0})$ .
At resonance $ω L = \frac{1}{ω C}$
$ω^{2} = \frac{1}{L C}$ (or) $ω = \frac{1}{\sqrt{L C}}$
$2 π f_{0} = \frac{1}{\sqrt{L C}}$
$f_{0} = \frac{1}{2 π \sqrt{L C}}$

In frequency response curve, at resonant frequency $(f_{0})$ , current is maximum. This series resonant circuit is called acceptor circuit.

Updated on:21/07/2023

In series LCR circuit at resonance
APower factor is zero
BPower developed across the resistor is maximum
CPower developed across the inductor is zero
DBoth (2) & (3)
In series LCR circuit at resonance,
Acurrent is maximum and impedance is maximum
Bcurrent is maximum and impedance is minimum
Ccurrent is minimum and impedance is maximum
Dcurrent is minimum and pmpedance is minimum
In series LCR circuit at resonance,
Acurrent is maximum and voltage is minimum
Bcurrent is maximum and voltage is maximum
Ccurrent is minimum and voltage is maximum
Dcurrent is minimum and voltage is minimum