State the basic postulates of Bohr's theory of atomic spectra. Hence obtain an expression for the radius of orbit and the energy of orbital electron in a hydrogen atom.

Text Solution

Verified by Experts

a) Basic postulates of Bohr's theory are
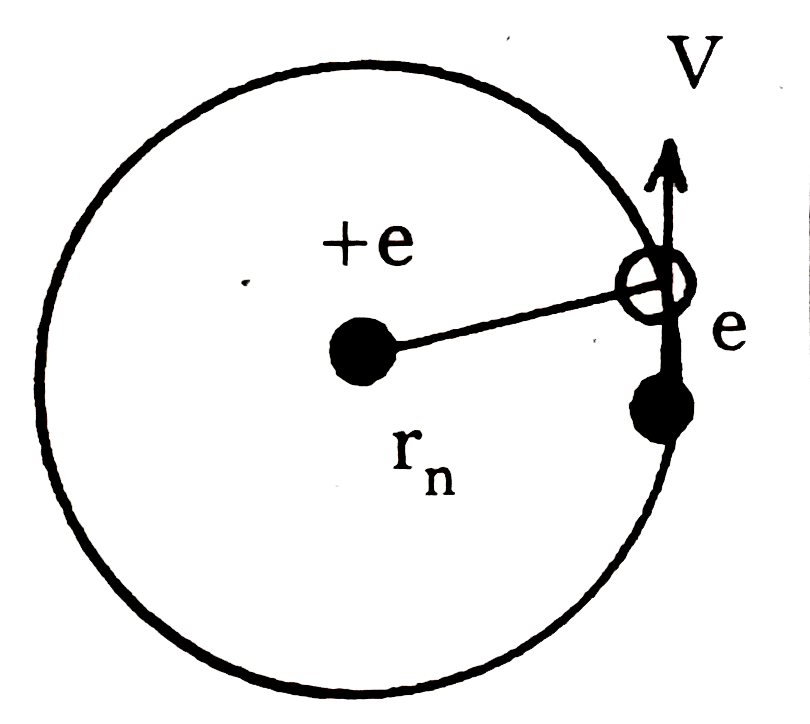
1) The electron revolves round a nucleus is an atom in various orbits known as stationary orbits. The electrons can not emit radiation when moving in their own stationary levels.
2) The electron can revolve round the nucleus only in allowed orbits whose angular momentum is the integral multiple of $\frac{h}{2 π}$
i.e., $m v_{n} r_{n} = \frac{n h}{2 π} \to (1)$
where n=1,2,3....
3) If an electron jumps from higher energy $(E_{2})$ orbit to the lower energy $(E_{1})$ orbit, the difference of energy is radiated in the form of radiation.
i.e., $E = h v = E_{2} - E_{1} \Rightarrow v = \frac{E_{2} - E_{1}}{h} \to (2)$
b) Energy of emitted radiation : in hydrogen atom, a single electron of charge-e, revolves around the nucleus of charge e in a circular orbit of radius $r_{n}$ .
1) K.E. of electron : For the electron to be in circular orbit, centripetal force = The electrostatic force of attraction between the electron and nucleus
From Coulomb's law, $\frac{m v_{n}^{2}}{r_{n}} = \frac{K e^{2}}{r_{n}^{2}} \to (3)$
where $K = \frac{1}{4 π ε_{0}} \to (4)$
$m v_{n}^{2} = \frac{K e^{2}}{r_{n}} \to (5)$
$m v^{2} r_{n} = K e^{2} \to (6)$
Dividing (5) by (1), $v_{n} = K e^{2} \times \frac{2 π}{n h}$
From (3), kinetic energy $K = \frac{1}{2} m v_{n}^{2} = \frac{K e^{2}}{2 r_{n}}$
2) Potential energy of electron :
P.E. of electron, $U = \frac{K e}{r_{n}} \times - e [∵ W = \frac{1}{4 π ε_{0}} \frac{q}{d} \times - Q]$
$∴ U = \frac{- K e^{2}}{r_{n}}$
3) Radius of the oribit : Substituting the value of (6) in (2).
$\frac{m}{r_{n}} (\frac{n^{2} h^{2}}{4 π^{2} r_{n}^{2} m^{2}}) = \frac{K e^{2}}{r_{n}^{2}}$
$r_{n} = \frac{n^{2} h^{2}}{4 π^{2} m K e^{2}} \to (1)$
$∴ r_{n} = 0.53 n^{2}$
4) Total energy $(E_{n})$ : Revolving electron posses K.E. as well as P.E.
i.e., $E_{n} = K + U = \frac{K e^{2}}{2 t} - \frac{K e^{2}}{t} = \frac{- K e^{2}}{2 r}$
$\Rightarrow E_{n} = \frac{- K e^{2}}{2 n^{2} h^{2}} \times 4 π^{2} m K e^{2} [∴ from (7)]$
But $K = \frac{1}{4 π ε_{0}}$
$∴ E_{n} = \frac{- {me}^{4}}{8 ε_{0}^{2} n^{2} h^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ATOMS

Topper's Solved these Questions

Similar Questions

VIKRAM PUBLICATION ( ANDHRA PUBLICATION)-ATOMS-long answer questions

Home
Ask Doubt
Profile