Answer the following questions, which help you understand the difference between Thomson's model and Rutherford's model better.
Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α- particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide ?
This suggests that scattering is predominantly due to a single collision increases with the number of target atoms which increases linearly with the thickness of the foil.
Topper's Solved these Questions
- ATOMSBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ATOMSEXERCISE - TEXTUAL EXERCISES
12 Videos
- ANDHRA PRADESH MARCH-2019BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ANDHRA PRADESH MARCH-2019EXERCISE - SECTION-C
3 Videos
- COMMUNICATION SYSTEMBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - COMMUNICATION SYSTEMEXERCISE - TEXTUAL EXERCISES
8 Videos
Similar Questions
Answer the following question , which help you understand the difference between Thomson's model and Rutherford's model better.
Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α - particles scatterd at moderate angles is proportional to t. What due does this linear dependence on t provide ?
View SolutionAnswer the following questions, which help you understand the difference between Thomson’s model and Rutherford’s model better.
(a) Is the average angle of deflection of -particles by a thin gold foil predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
(b) Is the probability of backward scattering (i.e., scattering of α-particles at angles greater than 90°) predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
(c) Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α-particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide?
(d) In which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scattering of α -particles by a thin foil?
View Solution
Knowledge Check
Read the following passage carefully and answer the questions
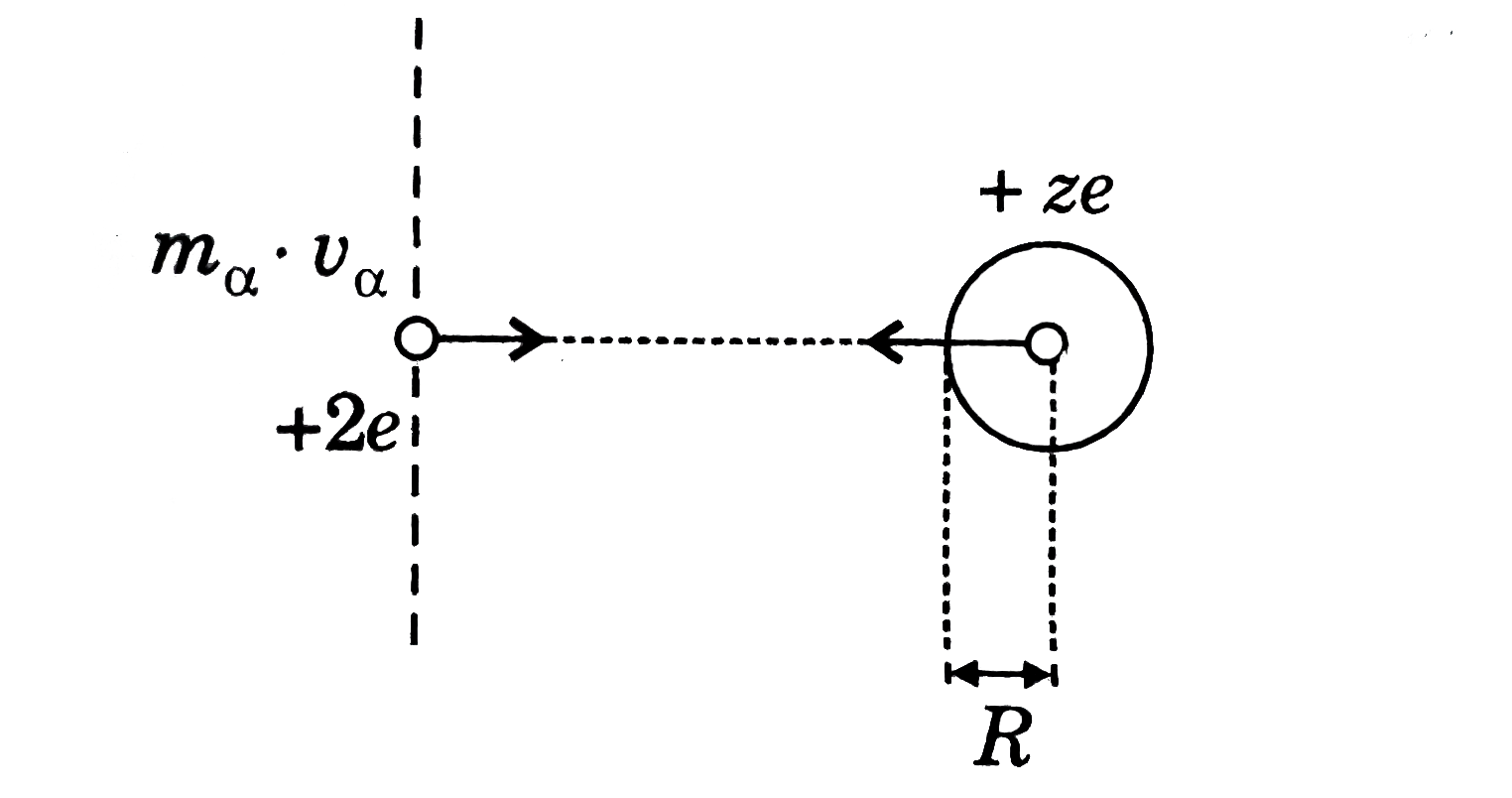
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
If α−particle with speed v0 is projected from infinity and it approaches upto r0 distance from the nuclei. Then the speed of α−particle which approaches 2r0 distance from the nucleus isA√2v0Bv0√2C2v0Dv02Read the following passage carefully and answer the questions
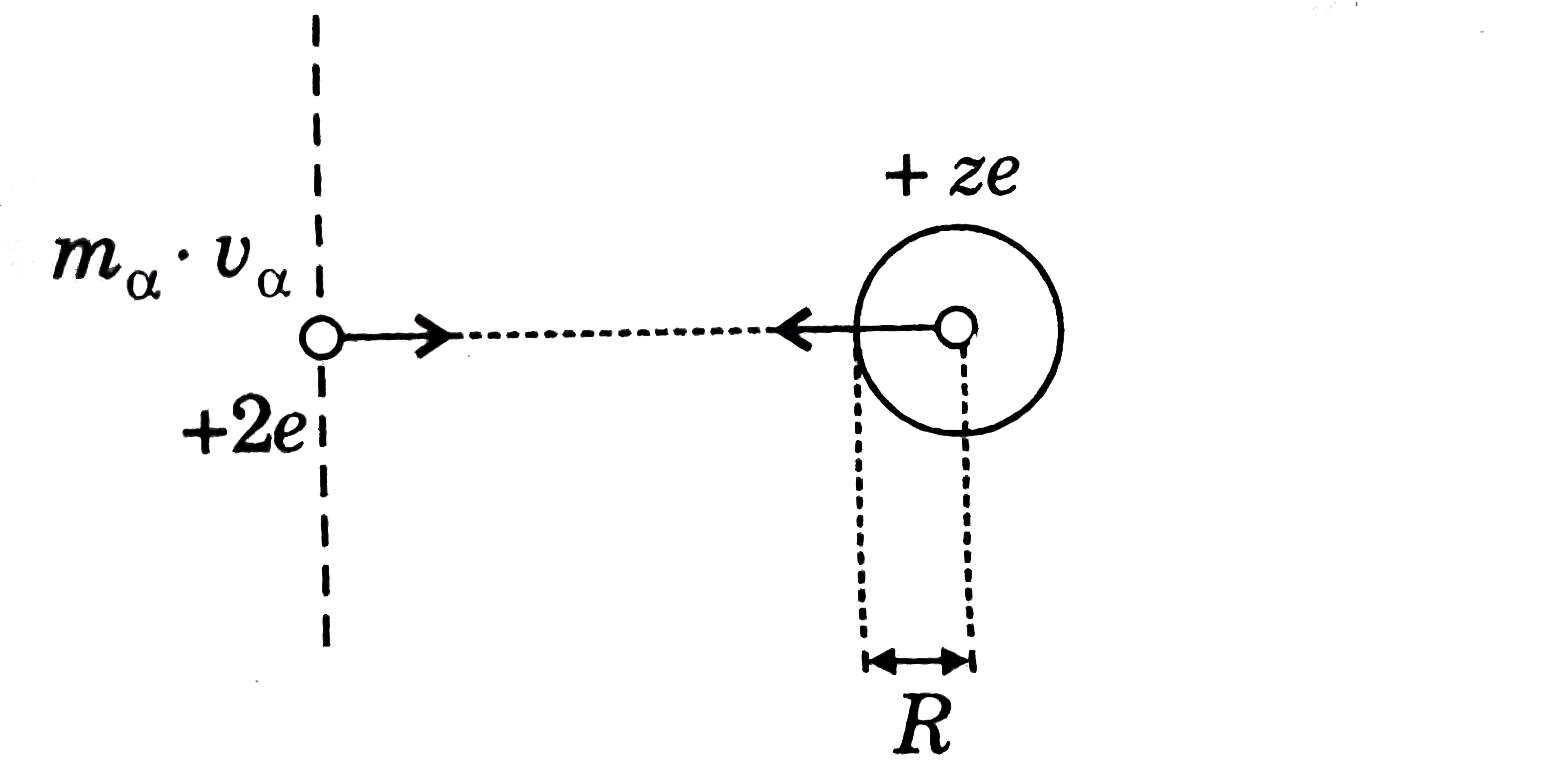
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
Radius of a particular nucleus is calculated by the projection of α−particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , α−particle with half of the earlier speed then the percentage error involved in the radius calculation is :A0.75B1C3D4
Answer the following questions, which help you understand the difference between Thomson’s model and Rutherford’s model better.
(a) Is the average angle of deflection of -particles by a thin gold foil predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
(b) Is the probability of backward scattering (i.e., scattering of α-particles at angles greater than 90°) predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
(c) Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α-particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide?
(d) In which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scattering of α -particles by a thin foil?
View SolutionAnswer the following question , which help you understand the difference between Thomson's model and Rutherford's model better.
In Which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scatterig of α - particles by a thin foil?
View SolutionAnswer the following question , which help you understand the difference between Thomson's model and Rutherford's model better.
Is the average angle of deflection of a particles by a thin gold foil predicted by Thomson's model much less, about the same, or much greater than that predicted by Rutherford's model ?
View SolutionAnswer the following question , which help you understand the difference between Thomson's model and Rutherford's model better.
Is the probaility of backward scattering (i.e., scattering of α - particle at angles greater than 90∘) perdicted by Thomsom's model much less , about the same , or much greater than the predicted by Thomson'n model much less , about the same , or much greater than that predicted by Rutheford's model ?
View SolutionRead the following passage and then answer questions (a) - (e) on the basis of your understanding of the passage and the related studied concepts.
Rutherford was the pioneer who established the existence of the atomic nucleus. Result of Geiger and Marsden experiment on the scattering of a-particles from thin gold foils, performed at Rutherford’s suggestion, revealed that the distance of closest approach to a gold nucleus of an a-particle of kinetic energy 5.5 MeV is about 4.0×10−14m. The said scattering effect was explained by Rutherford by assuming that the Coulombian repulsive force was solely responsible for scattering. Since the positive charge is confined to the nucleus, the actual size of the nucleus has to be less than 4.0×10−14m.
If we use a-particles of higher energies, the distance of closest approach to the gold nucleus will be still smaller. At some point the scattering will begin to be affected by the short range nuclear forces and differ from Rutherford’s calculations. From the distance at which deviations set it, nuclear size can be inferred.
(a) Define MeV and express its value in terms of SI unit of energy.
(b) What is distance of closest approach ?
(c) Write an expression for distance of closest approach of a-particle to a gold nucleus.
(d) What was Rutherford’s hypothesis regarding the existence of the atomic nucleus ?
(e) How can you show that volume of the nucleus of an element is proportional to its mass number ?
View SolutionRamnik is a student of class 9. One day he was studying a chapter of chemistry in the class alongwith other students. The teacher, Mr. Bhagi, told the students that the scientists James Chadwick J.J. Thomson and E. Goldstein had discovered three subatomic particles P, Q and R, respectively. He gave the characteristics of all these particles, their locations and arrangements in the atom. Mr. Bhagi also described the contributions of scientists Ernest Rutherford and Neils Bohr in this regard. After completing the discussion on this chapter, Mr. Bhagi asked Ramnik to answer the following question :
(a) What is the name of particle P ? What is the nature of charge on it ? State its location in tha atom
(b) What is the name of particle Q ? What is the nature of charge on it ? State its location in the atom
(c) What is the name of particle R ? What is the nature of charge on it ? State its location in the atom
(d) (i) Which of the particles P,Q and R is not present in an ordinary hydrogen atom
(ii) Which of the particles P,Q and R is not present in an alpha particle ?
(e) What is the total number of P and R particles present in one atom of an element known as ?
. (f) The number of particles Q in one neutral atom of an element is nineteen. How are these particles arranged in various energy levels in the atoms ?
(g) What values are displayed by Ramnik in this episode ?
View Solution
