An infinite dielectric sheet having charge density σ has a holeof radius R in it. An electrom is released from point P on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the plane of the sheet.
 .
.
The infinity charged sheet with a circular hole can be consider superposition of an infinite sheet of charge density σ and charged disc of charge density −σ . From the principle of superpoition, we have the following :
 ,
,  ,
, 
Net electric field at P is the vector sum of electric fields due to both infinite sheet of charge (→E1) and disc (→E2)
electric field due to infinite dielectric sheet is
→E1=σ2ε0(ˆi)
Electric field at the axis of a disc of radius R is
→E1=σ2ε0[1−x√x2+R2](−ˆi)
Resultant electric field is
→Enet=→E1+→E2=σ2ε0x√x2+R2(ˆi)
Force on the electron is
→F1=σex2ε0√x2+R2(ˆi)
mvdvdx=−σex2ε0√x2+R2
Let the speed of the electron when it crosses the sheet be v. Then
m∫v0vdv=−σe2ε0∫0√3Rx√x2+R2dx
or, mv22=σe2ε0[√x2+R2]0√3R
or, v=√σeRmε0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples10videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises58videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK19videos
COMMUNICATION SYSTEM
- BOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK40videos
Current Electricity
Similar Questions
An infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the center of the hole.
 View Solution
View SolutionA large metallic plate is facing a charged sheet having charge density σ placed parallel to plate at a distance l from the plate.Potential at point P at a distance x from the sheet is
View Solution
Knowledge Check
- Question 1 - Select One
There is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
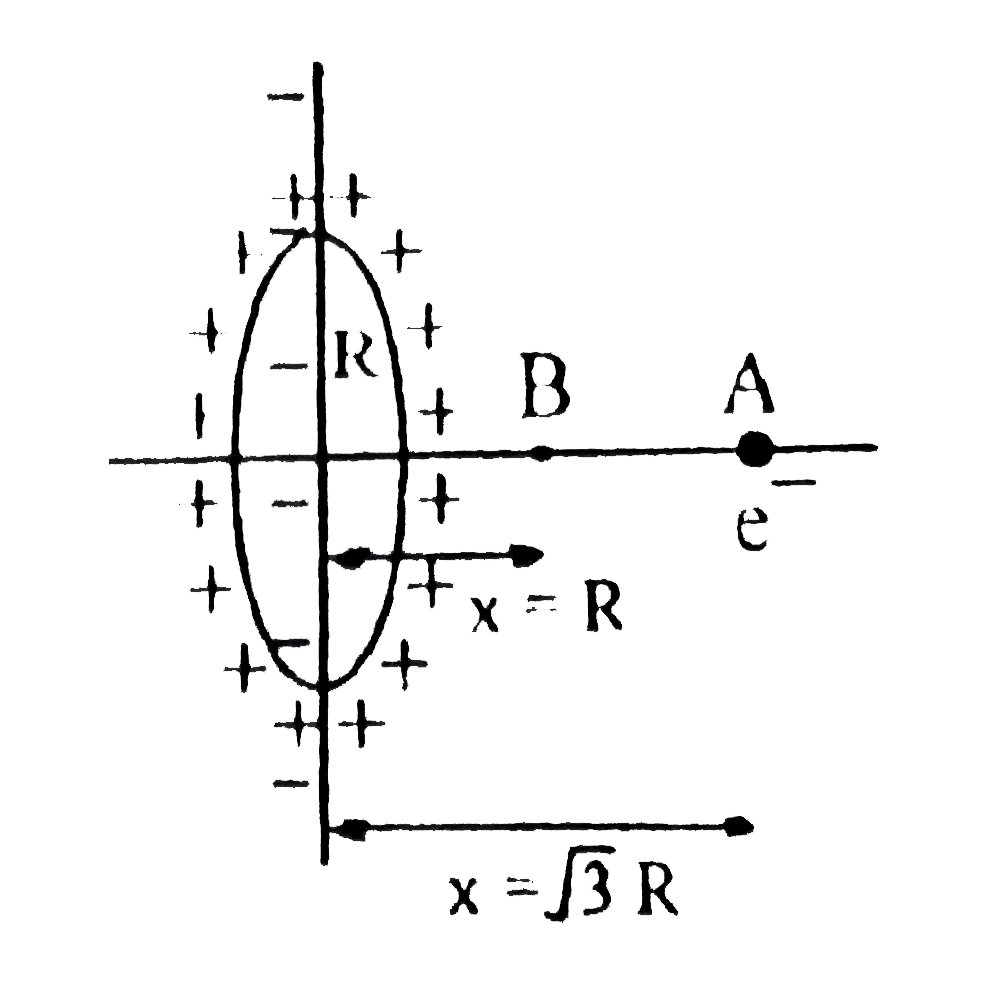
The distance from centre of ring on the axis where the net force on the electron is zero.A2RB√2RCRDnone of these - Question 2 - Select One
There is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
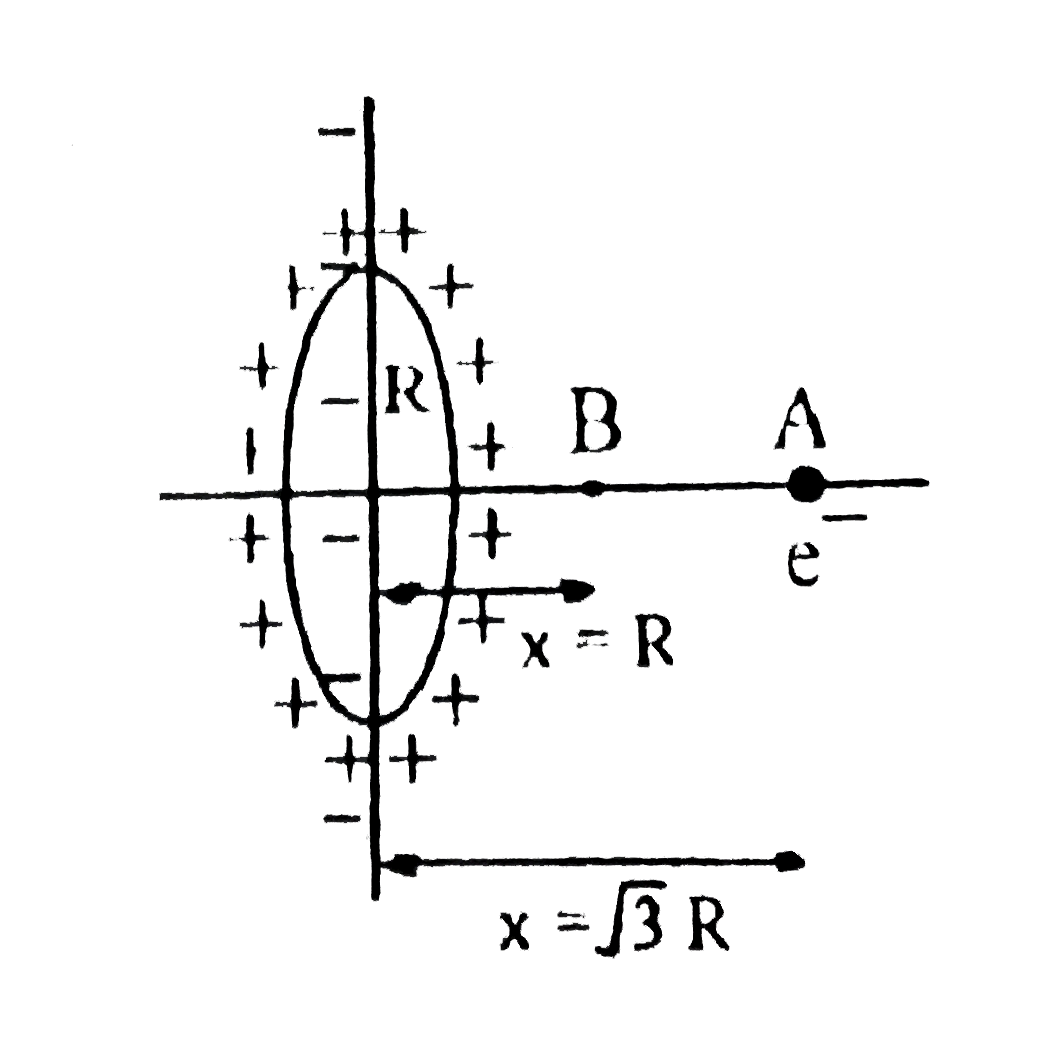
Potential difference between points A(x=√3R) and B(x=R)i.e.(VA−VB) isA−λπɛ0[(1−1√2)−ln34]B−λπɛ0[(1−1√2)−ln34]C−λπɛ0[(1+1√2)−ln34]Dnone - Question 3 - Select One
A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2
Potential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View SolutionAn infinitely large non-conducting plane of uniform surface charge density σ has circular aperture of certain radius carved out from it. The electric field at a point which is at a distance 'a' from the centre of the aperture (perpendicular to the plane) is σ2√2∈0. Find the radius of aperture :
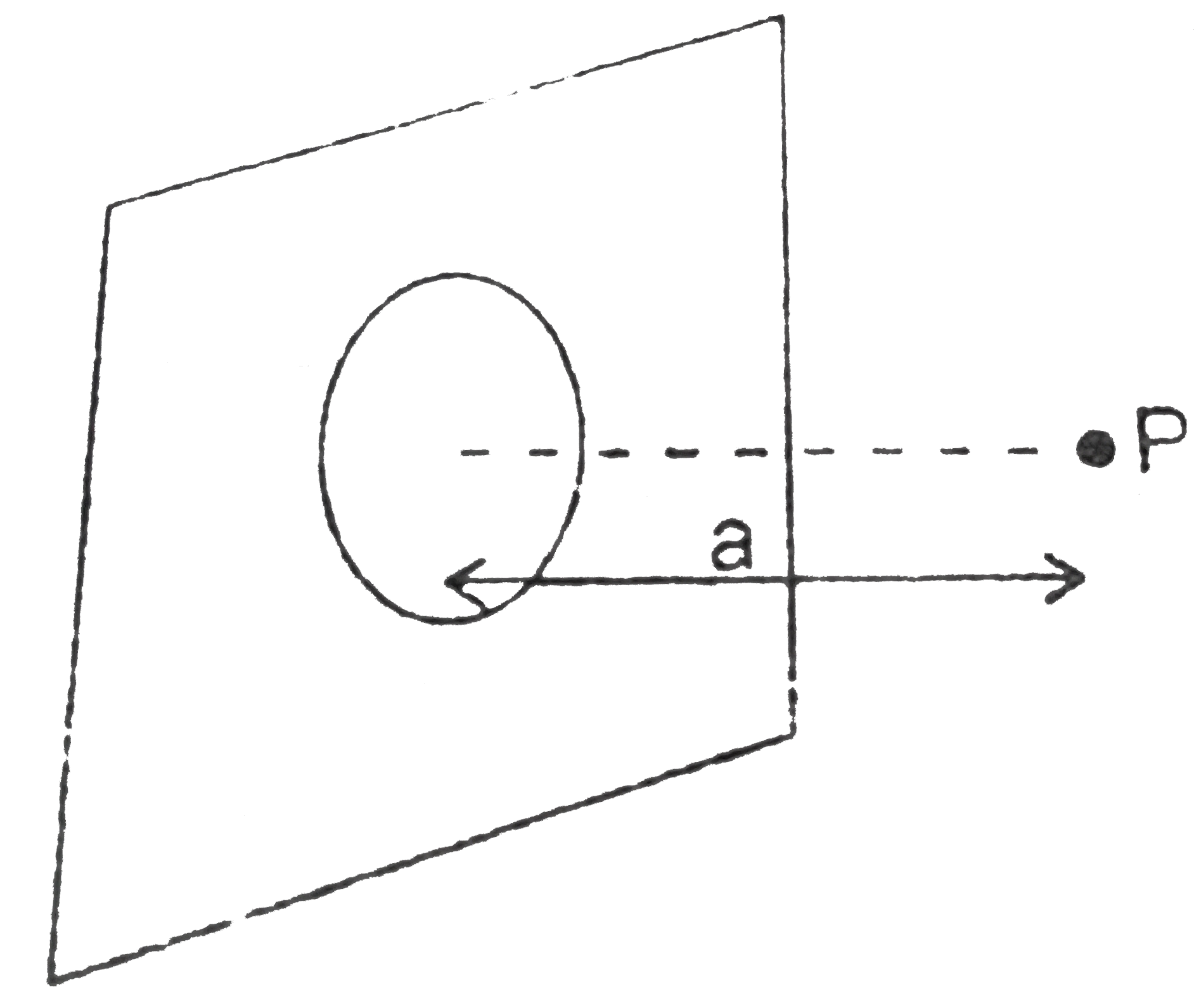 View Solution
View SolutionThere is an infinite non conducting sheet of charge having uniform charge density σ. The electric field at a point P at a distance x from the sheet is E0. Point O is the foot of the perpendicular drawn from point P on the sheet. A circular portio of radius r<<x centered at O is removed from the sheet. Now the field at point P becomes E0−ΔE. Find ΔE.
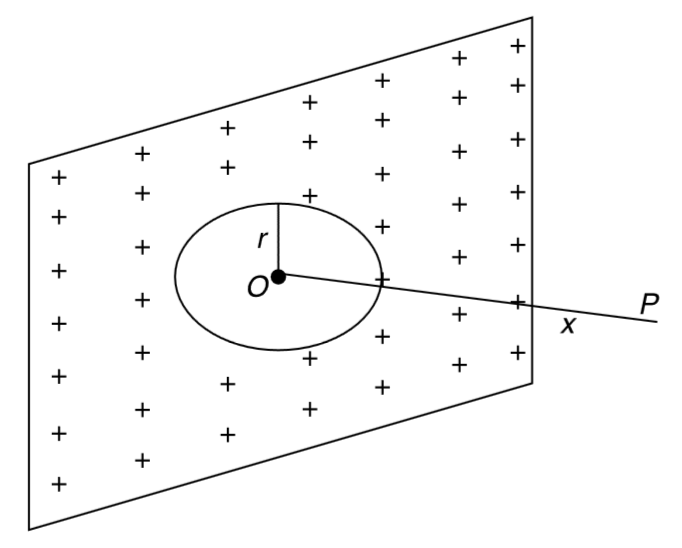 View Solution
View SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
 View Solution
View SolutionA large metallic plate is facing a charged sheet having charge density "sigma" placed parallel to plate at a distance "l" from the plate.Potential at "point "P" at a distance [x" from the sheet is "]
View Solution

