A particle of mass ma and charge q is released from rest in a uniform filed of magnitude E. the uniform field is created between two parallel plates of charge densities +σ and −σ, respectively. The particle accelerates toward the other plate a distance d apart. Determine the speed at which it stirkes the opposite plate.

The applied electric field is →E=−E0ˆj. The force experienced by the charge q is
→F=q→E=−qE0ˆj
The force is constant, and so the acceleration is constant as well, i.e.
→a=→Fm=−qE0mˆj
Because of constant acceleration the particle moves in the negative y-direction , the problem is analogous to the motion of a mass released from rest in a gravitational field. from equations of motion we get
vy=vy0+ayt=0−−qE0mt...(i)
and y=y0+v0t+12ayt2 or 0=d+0−12qE0mt2...(ii)
The particle starts at y0=d and impact occure at y=0 from eq. (ii) we get,
t=(2dmqE0)1/2
From eq. (i) we get
vy=−qE0m(2dmqE0)1/2=−√2qE0dm.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples
10 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- COMMUNICATION SYSTEMBOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK
19 Videos
- Current ElectricityBOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK
40 Videos
Similar Questions
A particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains afect moving a distance x between the plates.
View SolutionTwo large metal plates with surface charge densities +σ and −σ are separated from each other by a distance of d. Find the force per unit area acting between them.
View Solution
Knowledge Check
A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2r22mCEq2m2t2DEqm2tA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2t22mCEq2m2t2DEqm2tA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
A B
B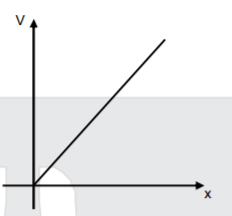 C
C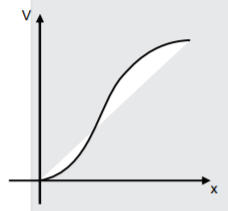 D
D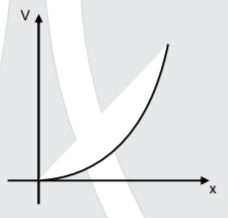
Two large parallel plane sheets have uniform charge densities + σand−σ. Determine the electric field (i) between the sheets, and (ii) outside the sheets.
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionTwo infinitely long parallel sheets having surface charge densities +σand−σ respectively are separated by a small distance. The electric field in the region between the plates is
View SolutionA charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
View SolutionThe surface charge densities on two square plates of a parallel plate capacitor are to +σand−σ respectively. What is the magnitude of the electric field in the region between the plates?
View Solution
