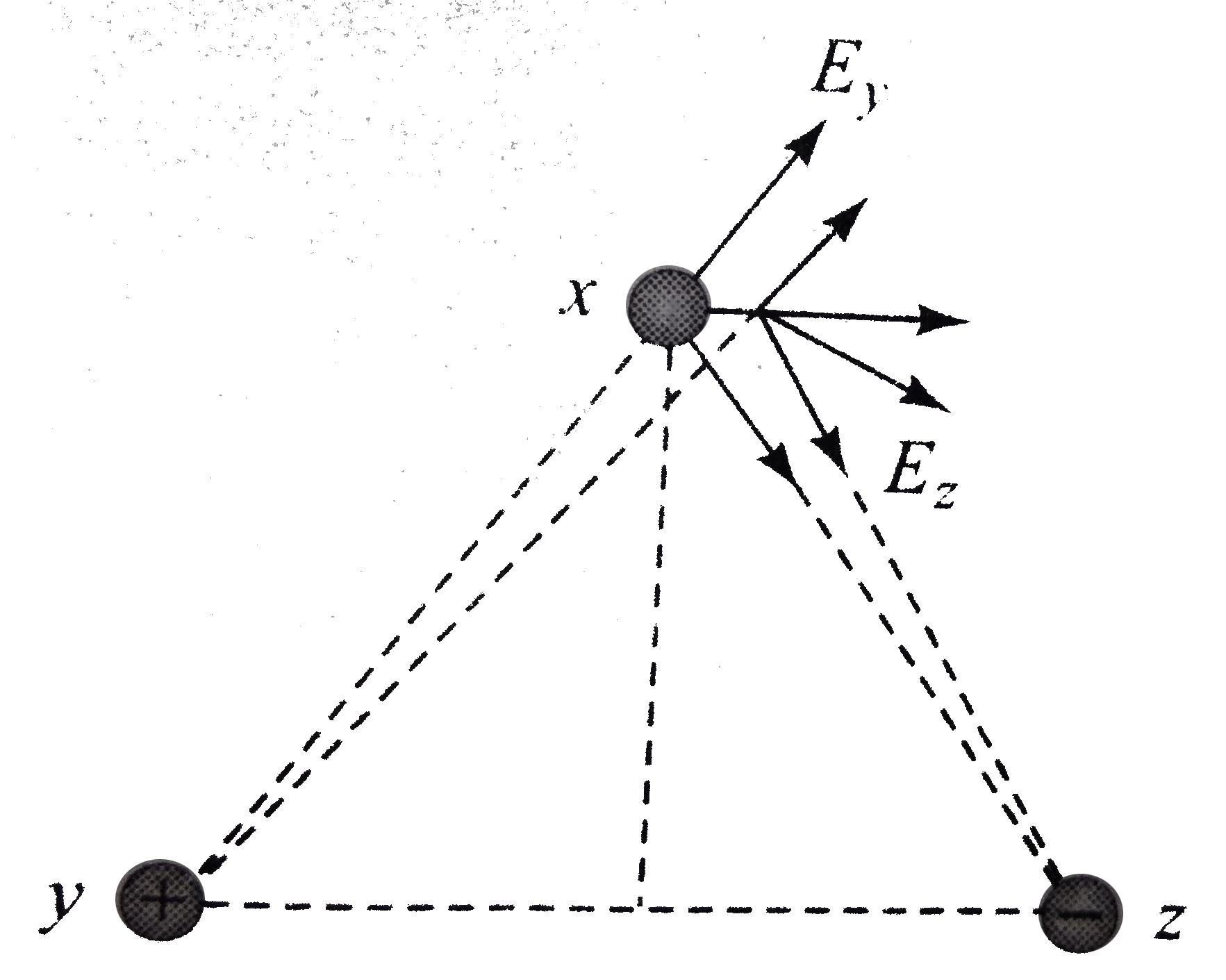
Three small spheres x,y, and z carry charges of equal magnitudes and with signs shown in fig. They are palced at the vertices of an isosceles triangle with the distance betwwen x and y equal to the distance between x and z. sphere y and z are held in place, but sphere x is free to move on a frictionless surface.
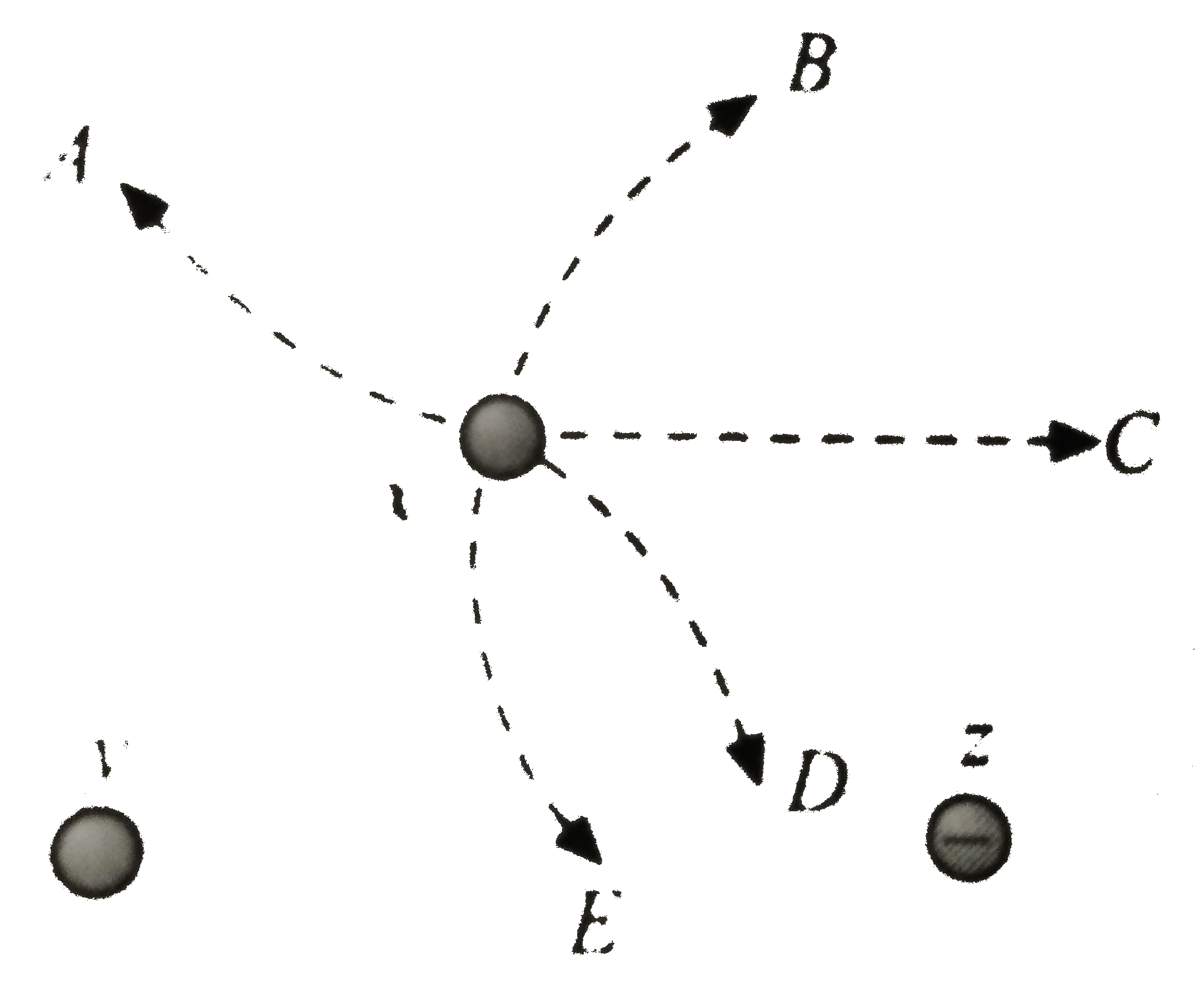
(a) waht is the direction of hte electric force on sphere x at the point shown in the figure?
(b) Which path is sphere x likely to take when released?
Video Solution
Text Solution
(a) along C.
(b) Path D. As x starts moving, the magnitude of electric field dureto charge on z increases. The resultant electric field chages the direction asshown in the figure. Hence, we can say the charge particle follows path D.
|
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Subjective
Explore 32 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Correct
Explore 47 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Solved examples
Explore 10 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Knowledge Check
The distance between the planes 3x+5y+z=8 and 3x+5y+z+27=0 is :
A8√35B27√35C√35D2√35The lines x=y=z meets the plane x+y+z=1 at the point P and the sphere x2+y2+z2=1 at the point R and S, then
APR+PS=2BPR×PS=23CPR=PSDPR+PS=RSThe length of the base of an isosceles triangle is 2x−2y+4z, and its perimeter is 4x+6z. Then the length of each of the equal sides is
Aa)x+yBb)x+y+zCc)2(x+y)Dd)x+z
The shortest distance between the lines x+a=2y=−12zandx=y+2a=6z−6a is
View SolutionThe shortest distance between the lines x=y+2 = 6z-6 and x + 1 = 2y = - 12z is
View SolutionThe shortest distance between the line 1+x=2y=-12z and x=y+2=6z-6 is
View SolutionThe shortest distance from the point (1,2−1) to the surface of the sphere x2+y2+z2=54 is
View SolutionThe shortest distance between the lines 2x+y+z−1=0=3x+y+2z−2 and x=y=z, is
View Solution