A long, straight wire is surrounded by a hollow metal cylinder whose axis coincides with that of the wire. The wire has a charge per unit length of λ, and the cylinder has a net charge per unit length of 2λ. From this information, use Gauss's law to find (i) the charge per unit length on the inner and outer surfaces of the cylinder and (ii) the electric field outside the cylinder, a distance r from the axis.
To solve the problem step by step, we will use Gauss's law to find the charge per unit length on the inner and outer surfaces of the hollow metal cylinder and the electric field outside the cylinder.
Step 1: Understanding the Setup
We have a long straight wire with a charge per unit length of λ and a hollow metal cylinder with a net charge per unit length of 2λ. The wire is placed along the axis of the cylinder.
Step 2: Charge Distribution on the Cylinder
1. Inner Surface Charge:
- The electric field inside a conductor in electrostatic equilibrium is zero. Therefore, the charge on the inner surface of the cylinder must be such that it cancels the electric field due to the wire.
- Let the charge per unit length on the inner surface of the cylinder be λ′.
- The total charge enclosed by a Gaussian surface just inside the cylinder (which encloses the wire) is λ.
- According to Gauss's law, the electric field E inside the conductor is given by:
E⋅A=Qenclosedϵ0
- Since E=0 inside the conductor, we have:
0=λ′+λ
- Thus, λ′=−λ.
2. Outer Surface Charge:
- The total charge per unit length of the cylinder is given as 2λ.
- The charge on the outer surface λ′′ can be found using the total charge:
λ′+λ′′=2λ
- Substituting λ′=−λ:
−λ+λ′′=2λ
- Solving for λ′′:
λ′′=3λ
Step 3: Summary of Charges
- Charge per unit length on the inner surface of the cylinder: λ′=−λ
- Charge per unit length on the outer surface of the cylinder: λ′′=3λ
Step 4: Electric Field Outside the Cylinder
To find the electric field outside the cylinder at a distance r from the axis, we again apply Gauss's law.
1. Gaussian Surface: Consider a cylindrical Gaussian surface of radius r (where r is greater than the radius of the hollow cylinder) and length L.
2. Total Charge Enclosed:
- The total charge enclosed by this Gaussian surface is the sum of the charge on the wire and the charge on the outer surface of the cylinder:
Qenclosed=λL+3λL=4λL
3. Applying Gauss's Law:
- The electric field E times the surface area of the cylindrical Gaussian surface gives:
E⋅(2πrL)=Qenclosedϵ0
- Substituting Qenclosed:
E⋅(2πrL)=4λLϵ0
- Dividing both sides by 2πrL:
E=4λ2πϵ0r=2λπϵ0r
Final Answers
1. Charge per unit length on the inner surface of the cylinder: −λ
2. Charge per unit length on the outer surface of the cylinder: 3λ
3. Electric field outside the cylinder at a distance r:
E=2λπϵ0r
We have a long straight wire with a charge per unit length of λ and a hollow metal cylinder with a net charge per unit length of 2λ. The wire is placed along the axis of the cylinder.
1. Inner Surface Charge:
- The electric field inside a conductor in electrostatic equilibrium is zero. Therefore, the charge on the inner surface of the cylinder must be such that it cancels the electric field due to the wire.
- Let the charge per unit length on the inner surface of the cylinder be λ′.
- The total charge enclosed by a Gaussian surface just inside the cylinder (which encloses the wire) is λ.
- According to Gauss's law, the electric field E inside the conductor is given by:
E⋅A=Qenclosedϵ0
- Since E=0 inside the conductor, we have:
0=λ′+λ
- Thus, λ′=−λ.
- The total charge per unit length of the cylinder is given as 2λ.
- The charge on the outer surface λ′′ can be found using the total charge:
λ′+λ′′=2λ
- Substituting λ′=−λ:
−λ+λ′′=2λ
- Solving for λ′′:
λ′′=3λ
- Charge per unit length on the inner surface of the cylinder: λ′=−λ
- Charge per unit length on the outer surface of the cylinder: λ′′=3λ
To find the electric field outside the cylinder at a distance r from the axis, we again apply Gauss's law.
2. Total Charge Enclosed:
- The total charge enclosed by this Gaussian surface is the sum of the charge on the wire and the charge on the outer surface of the cylinder:
Qenclosed=λL+3λL=4λL
3. Applying Gauss's Law:
- The electric field E times the surface area of the cylindrical Gaussian surface gives:
E⋅(2πrL)=Qenclosedϵ0
- Substituting Qenclosed:
E⋅(2πrL)=4λLϵ0
- Dividing both sides by 2πrL:
E=4λ2πϵ0r=2λπϵ0r
1. Charge per unit length on the inner surface of the cylinder: −λ
2. Charge per unit length on the outer surface of the cylinder: 3λ
3. Electric field outside the cylinder at a distance r:
E=2λπϵ0r
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
Similar Questions
Knowledge Check
The charge deposited per unit length of cylinder is called as
Alinear charge densityBsurface charge densityCcharge densityDall of theseThe electric field at a distance r from a long wire having charge per unit length λ is
Ak(λr2)Bk(λr)Ck(λ2r)Dk(2λr)The charge per unit length of the four quadrant of the ring is 2λ,−2λ,λ and −λ respectively. The electric field at the centre is:
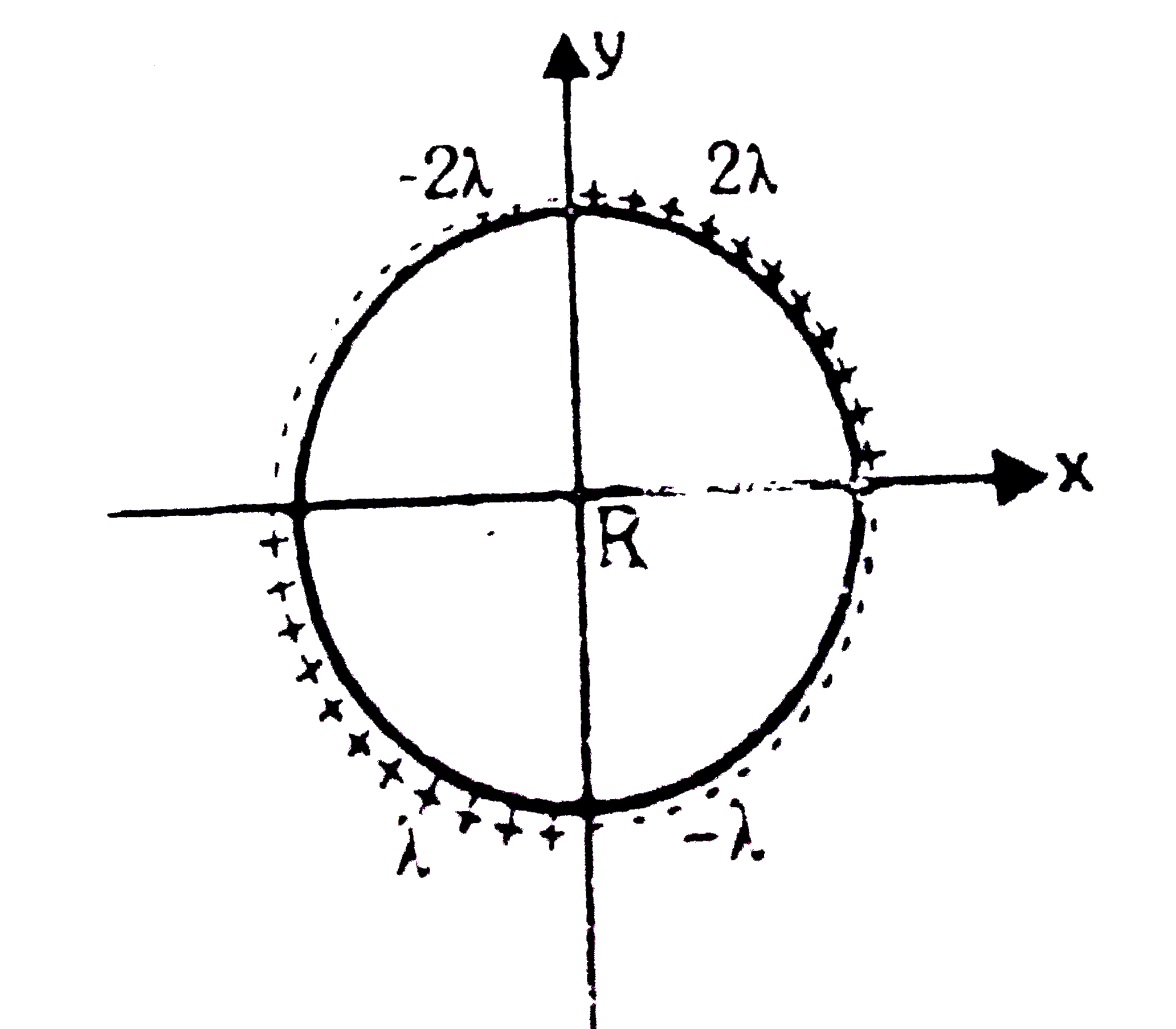 A−λ2πε0RˆiBλ2πε0RˆjC√2λ4πε0RˆiDNone
A−λ2πε0RˆiBλ2πε0RˆjC√2λ4πε0RˆiDNone
Calculate the potential due to a thin charged rod of length L at the points along and perpendicular to the length. Charge per unit length on the rod is λ.

View SolutionIn the previous question , if the conductor has a charge per unit length λ , the particle has mass m and charge q then (choose the correct option)
View SolutionThe electric field at a distance r from a long wire having charge per unit length λ is
View SolutionA wire is bent to form a semi circle such that the radius of the semicircle is R. The charge per unit length is λ. The total electric field at the centre will be
View SolutionA semicircular are of radius a is charged uniformly and the charge per unit length is λ. The electric field at its centre is
View Solution
