Two conducting plates A and B are placed parallel to each other. A is given a charge Q1 and B a charge Q2. Prove that the charges on the inner surfaces are of equal magnitude and opposite sign.
Consider a Gaussian surface as shown in figure.
Two faces of this closed surface lie completely inside the conductor
where the elctric field is zero. The flux through these faces
is, therefore, zero. The other parts of the closed surface, which
are outside the conductor, are parallel to the electric field, and
hence the flux on these parts is also zero. The total fulx of the
electric field through the closed surface is, therefore, zero.

From Gauss's law, the total charge inside this closed surface
should be zero. Thus , x+y=0orx=−y
Hence, the charge on the inner surface of A should be equal
and opposite to that on the inner surface of B.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
Similar Questions
Two conducting plates A and B are placed parallel to each other. A is given a charge. Q1 and B a charge Q2. Find the distribution of charges on the four surface.
View SolutionThree large plates A, B and C are placed parallel to each other and charges are given as shown. The charge that appears on the left surface of plate B is
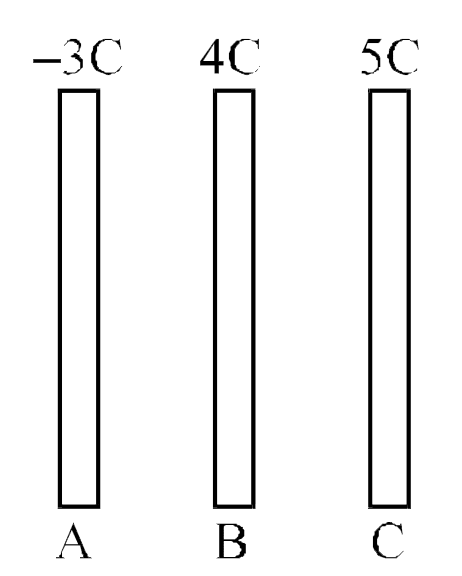
View Solution
Knowledge Check
Two large conducting plates are placed parallel to each other with a separation of d between them. An electron starting from rest near one of the plates reaches the other plate in time t. If e is the charge on the electron and m is its mass, then the surface charge density on the inner surface is
Adme4πε0t2Bdmε04πet2C2dmε0et2DNone of the aboveTwo conducting plates M and N, each having large surface area A (on one side), are placed parallel to each other in figure. The plate M is given charge Q1 and N, charge Q2(<Q1). Then
 Aelectric field at point A is (Q1−Q2)/2Aε0 toward right.Belectric field at point B is (Q1−Q2)/2Aε0 toward right.Celectric potential of N is greater than M.Dall of the above
Aelectric field at point A is (Q1−Q2)/2Aε0 toward right.Belectric field at point B is (Q1−Q2)/2Aε0 toward right.Celectric potential of N is greater than M.Dall of the aboveIn a parallel plate capacitor with plate area A and charge Q, the force on one plate because of the charge on the other is equal to
AQ2ε0A2BQ22ε0A2CQ2ε0ADQ22ε0A
Two large conducting plates X and Y. each having large surface area A (on one side), are placed parallel to each other as shown in figure (30-E7). The plate X ia given a charge Q whereas the other is neutral. Find (a) the surface charge dendity at the inner surface of the plates X, (b) the electric field at a point to the left of the plates, (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.

View SolutionA and B are two large identical thin metal plates placed parallel to each other at a small separation. Plate A is given a charge Q. (i) Find the amount of charge on each of the two faces of A and B. (ii) Another identical plate C having charge 3Q is inserted between plate A and B such that distance of C from B is twice its distance from A. Plate A and B is shorted using a conducting wire. Find charge on all six faces of plates A, B and C. (iii) In the situation described in (ii) the plate A is grounded. Now write the charge on all six faces.
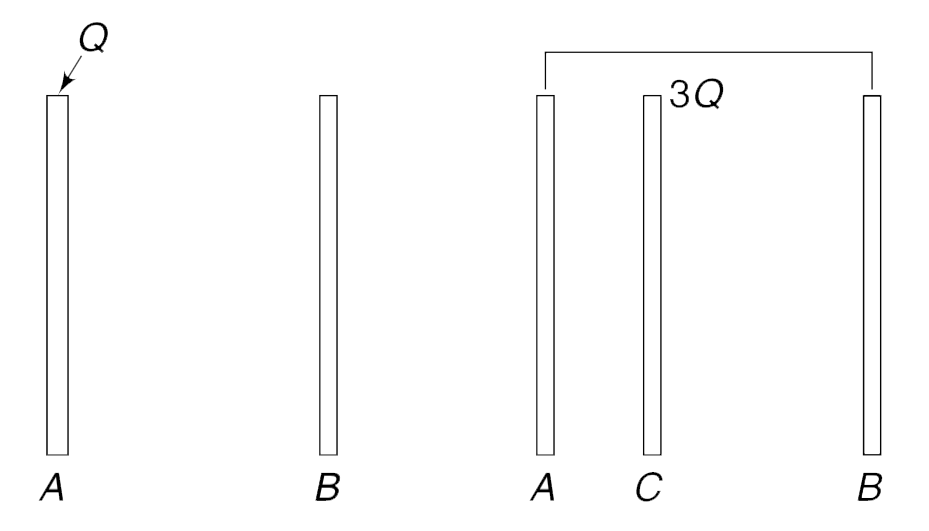
View SolutionTwo conducting plates X and Y, having large surface area A (on one side), are placed parallel to each other as shown in figure. The plate X is given a charge Q whereas the other is neutral. Find :
(a) The surface charge density at the inner surface of the plate X,
(b) The electric field at a point to the left of the plates,
(c) The electric field at a point in between the plates and
(d) The electric field at a point to the right of the plates.
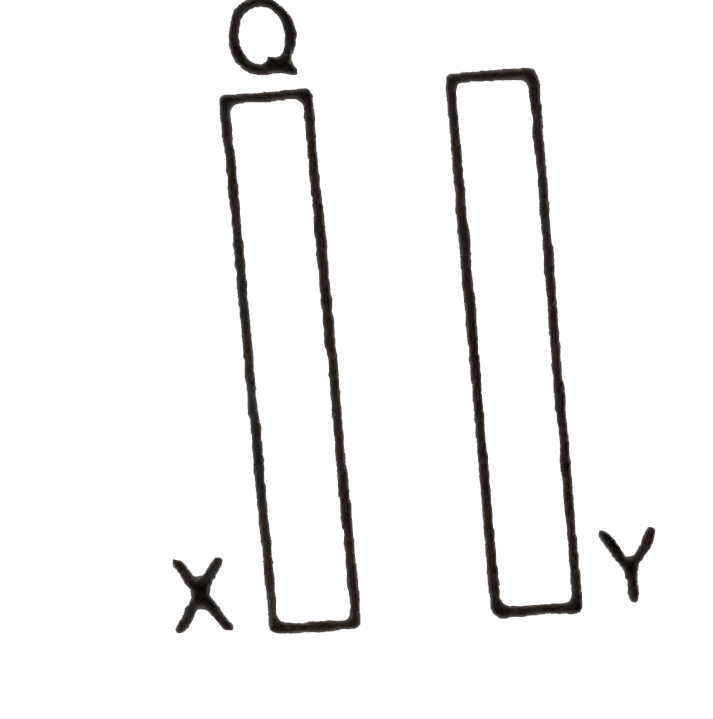
View SolutionThere are two large conducting plane sheets. Both of them are given charges Q1 and Q2 . What is the charge distribution on their surfaces, when they are (i) large distance apart (ii) brought close and placed parallel to each other ?
View SolutionTwo large parallel conducting plates are placed close to each other ,the inner surface of the two plates have surface charge densities +σ and −σ .The outer surfaces are without charge.The electric field has a magnitude of
View Solution
