Figure shows three metallic plates with charges Q, 4Q, and -Q, respectively. Determine the final charges on all the surfaces.
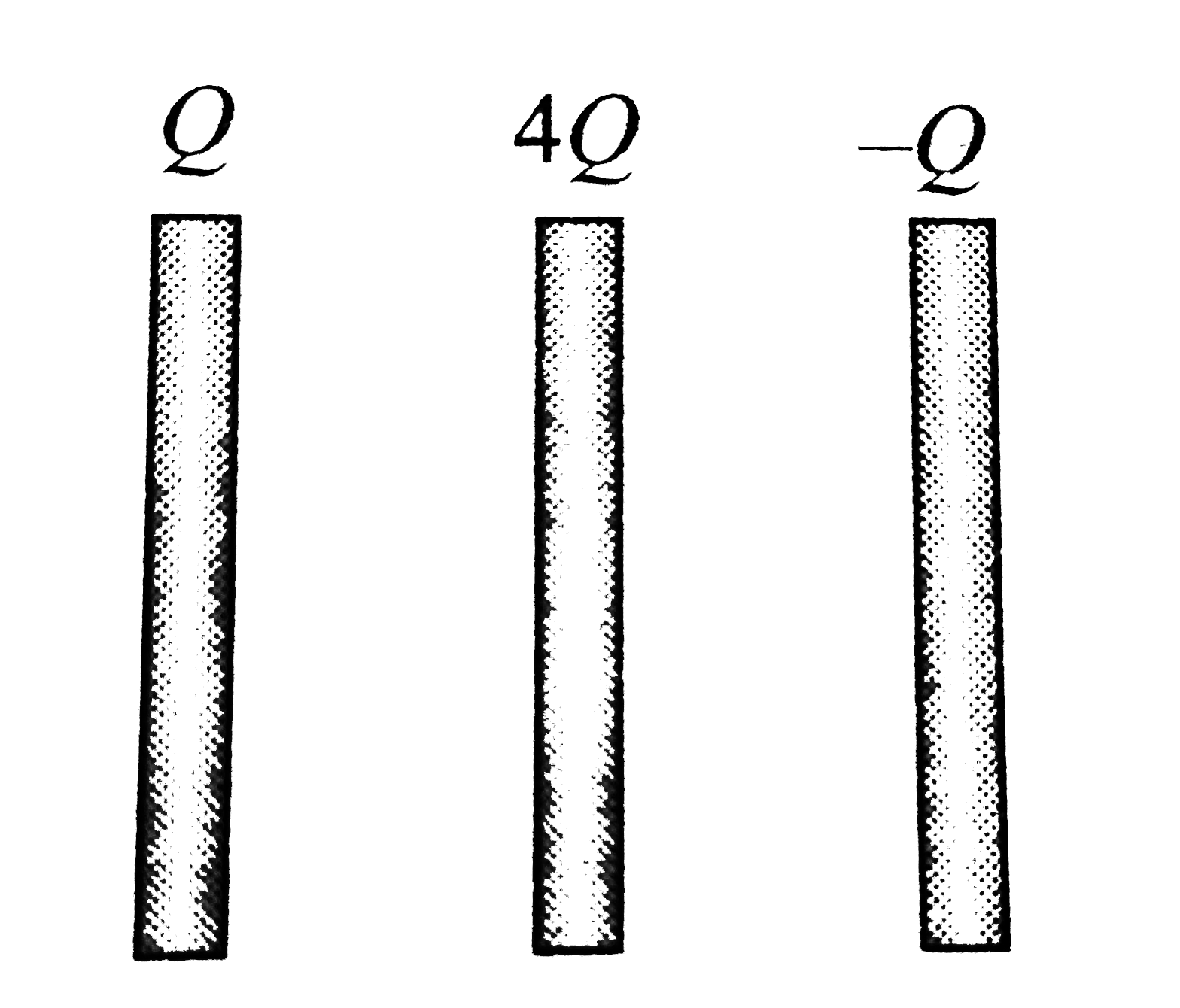
Method 1: We assume that the charge
on surface 2 is x. Following conservation
of charge, we see that surface 1 has charge (Q-x). The electric
field inside the metal plate is zero, so field at P is zero.
So the resultant field at P is −EP=
⇒(Q−x2Aε0)=x+4Q−Q2Aε0
or Q−x=x+3Q
or x=−Q
The charges on the facing
surfaces of the plates are of
equal magnitude and opposite
sign. This can be proved by
Gauss's theorem also. It is an
important result.
Thus, the final charge
distribution on all the surfaces
is shown in figure.

Method 2: The electric field
due to an infinite sheet of charge
is independent of distance. We
can take plates (ii) and (iii) as
one system or one plate having
charge 4Q−Q=3Q.

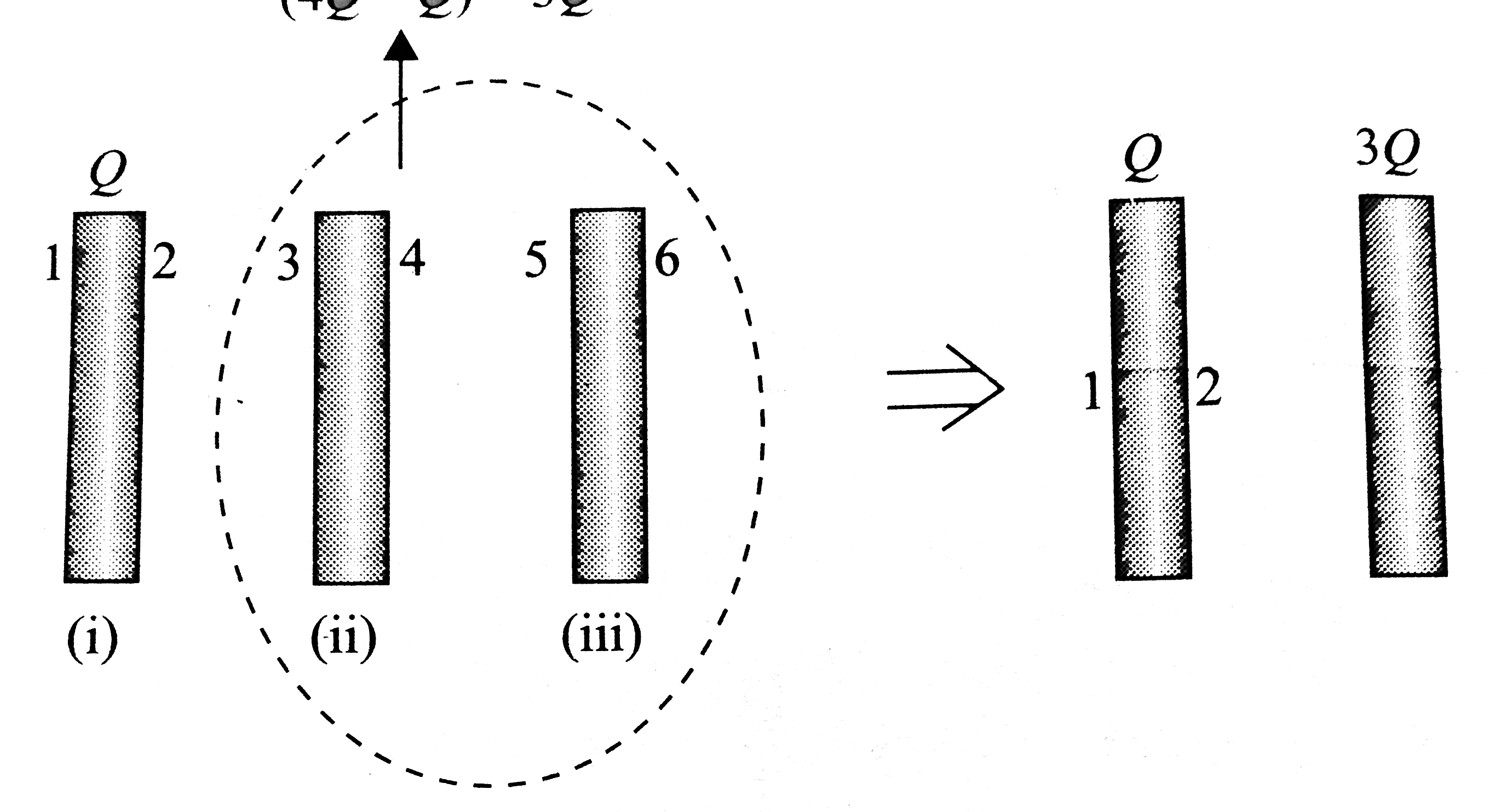
The charge appearing on surface (2) is
q2=Q−3Q2=−Q
Hence, final charge distribution is same as we calculated in
method 1.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example7videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.116videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.514videos
ELECTRIC POTENTIAL
Similar Questions
Figure shows three large metallic plates with chrges −Q,3Q and Q respectively. Determine the final charges on all the surfaces.
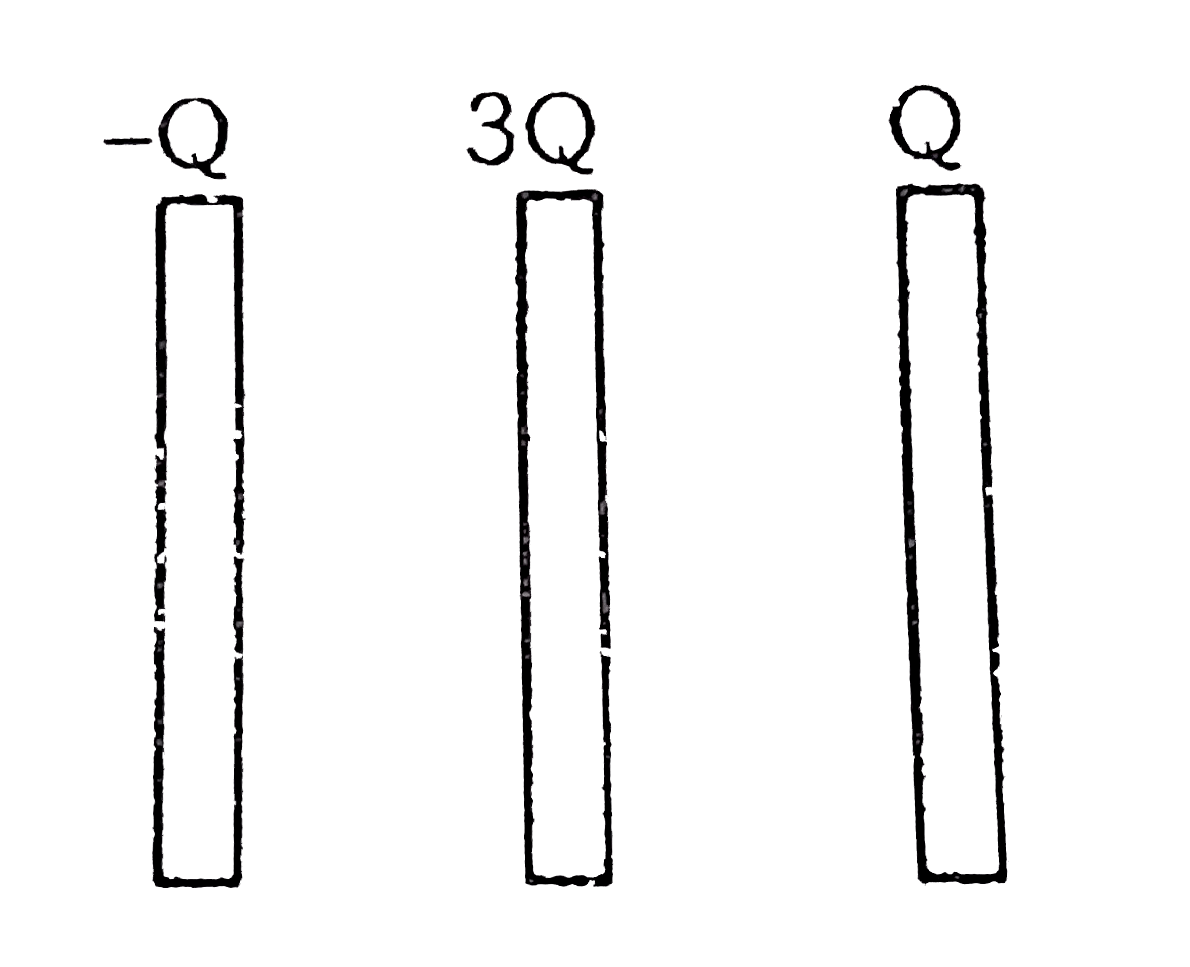 View Solution
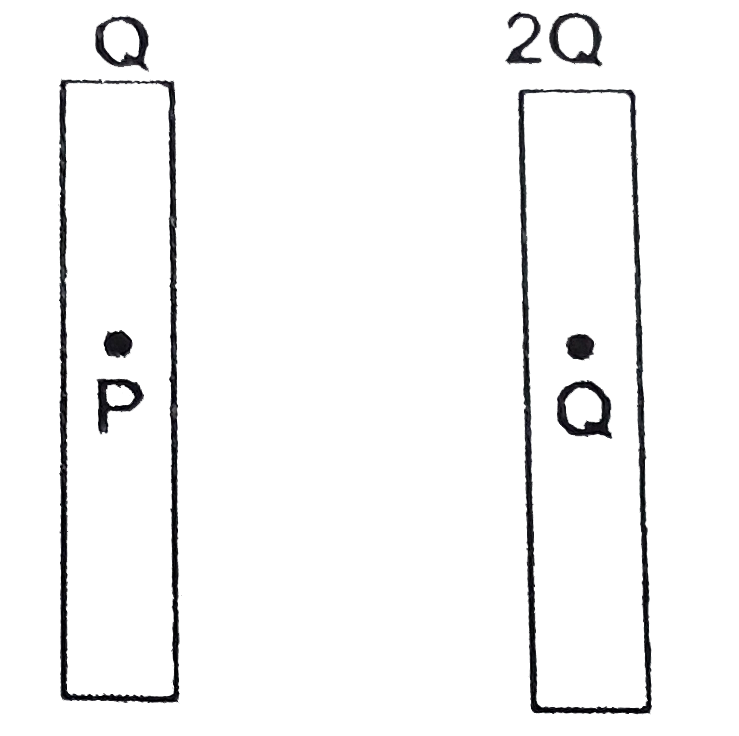
View SolutionTwo large parallel conducting sheets (placed at finite distance) are given charges Q and 2Q respectively. Find out charges appearing on all the surfaces.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three concentric metallic spherical shells of radii R, 2R, 3R, are given charges Q1, Q2, Q3, respectively. It is found that the surface charge denisties on the outer surfaces of the shells are equal. Then, the ratio of the charges given to the shells, Q1:Q2:Q3, is
A(a) 1:2:3B(b) 1:3:5C(c) 1:4:9D(d) 1:8:18 - Question 2 - Select One
Two concentric spherical shells of radii R and 2R are given charges Q1andQ2 respectively.
The surfaces charge densities of the outer surfaces are equal. Determine the ratio Q1:Q2.A1:2B4:1C1:4D2:1 - Question 3 - Select One
Three concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
A1:2:3B1:3:5C1:4:9D1:8:18
Figure shows three concentric thin conducting spherical shells A, B and C of radii R, 2R and 3R. The shell B is earthed A and C are given charges q and 2q respectively. Find the charges appearing on all the surface of A,B and C.

[inner surface (A)0,(B)−q,(C)43q
Outer surface (A)q,(B)−43q,(C)23q]View SolutionThree identical metal square plates of surface area A of each side is arranged as shown in the figure.Plates 1 2 and 3 are given charges +20, -Q and -Q respectively. Find out the correct options A) Charge on the two faces of the middle plate are -2Q and Q B) Charge on the two faces of the middle plate are -Q and 0 C) Charge on the two faces of the left most plate are zero and 2Q D) Charge on the two faces of the right most plate are -Q and zero
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.
 View Solution
View SolutionThree identical metallic plates are kept parallel to one another at a separation of a and b The outer plates are connected by a thin conducting wire and a charge Q is placed on the central plate Find final charges on all the surfaces of the three plates.
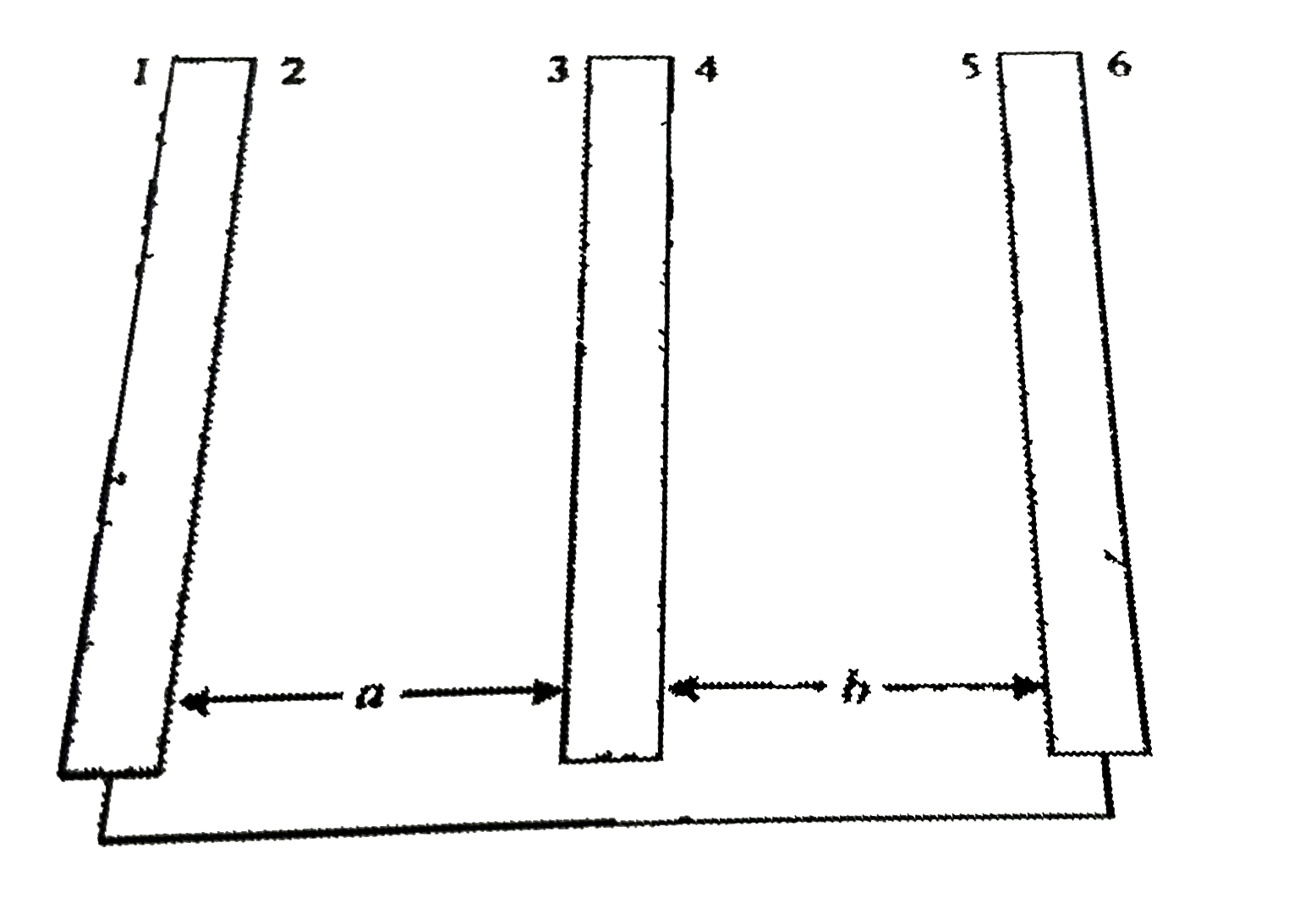
[faces(1)Q2,(2)−Qba+b,(3)Qba+b,(4)Qaa+b,(5)−Qaa+b,(6)Q3]View SolutionThree large conducting plates with charges Q,−Q and Q are kept close to each other as shown in the figure. ( where Q=2uc). Now all the three plates A, B, and C are connected by a thin conducting wire. Find the charge ( in C) on left surface of plate A at electristatic equailibrium
View Solution

