The three small spheres as shown in figure carry charges q1=4nC,q2=−7.8nCandq3=2.4nC. Find the net electic flux through each of the following closed surfaces shown in cross section in the figure.
a. S1 b.S2
c. S3 d. S4
e. S5.
Do your answers to parts from (a) to (e) depend on how the charge is distributed over each small sphere? Why or why not?
 .
.
a. ΦS1=q1/ε0=(4.00×10−9C)/ε0=452Nm2/C
b. ΦS2=q2/ε0=(−7.80×10−9C)/ε0=−881Nm2/C
c. ΦS3=(q1+q3)/ε0=((4.00−7.80)×10−9C)/ε0
=−429Nm2/C
d. ΦS4=(q1+q3)/ε0=((4.00+2.40)×10−9C)/ε0
=723Nm2/C
e. ΦS5=q1+q2+q3ε0=(4.00−7.80+2.40)×10−9Cε0
=−158Nm2/C
All that matters for Gauss's law is the total
amount of charge enclosed by the surface, not its
distribution within the surface.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective12videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Single Correct40videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.116videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.514videos
ELECTRIC POTENTIAL
Similar Questions
Three parallel metalic plates each of area A are kept as shown in figure and charges q1,q2 and q3 are given to them. Find the resulting charge distribution on the six surfaces, neglecting edge effects as usual,
 View Solution
View SolutionFig shows three point charges +2q,−qand+3q, What is the electric flux due to this configuration thorugh the surface S ?
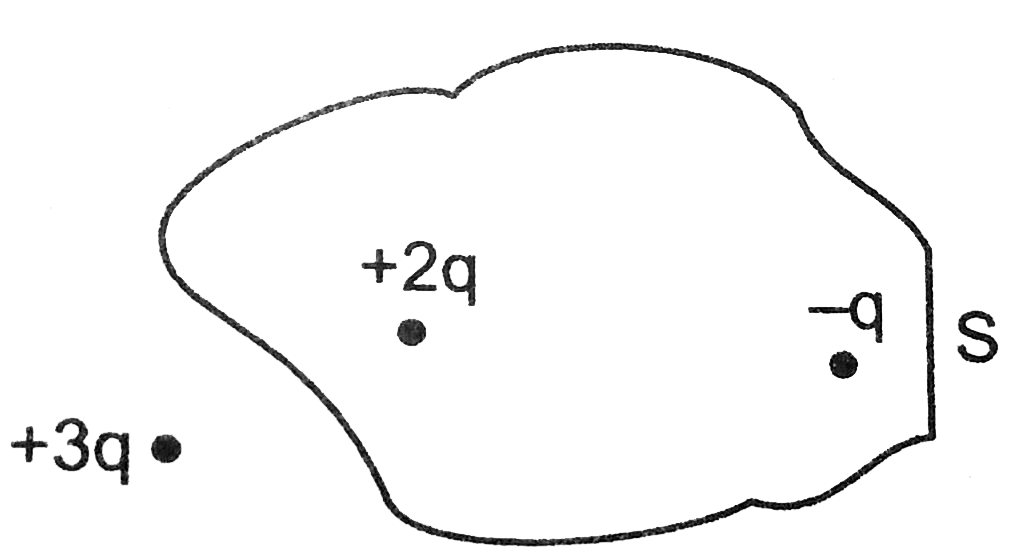 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows four charges q1,q2,q3,andq4 fixed is space. Then the total flux of the electric field through a closed surface S, due to all the charges, is
 Anot equal to the total flux through S due to q3andq4Bequal to the total flux through S due to q3andq4Czero if q1+q2=q3+q4Dtwice the total flux through S due to q3andq4ifq1+q2=q3+q4.
Anot equal to the total flux through S due to q3andq4Bequal to the total flux through S due to q3andq4Czero if q1+q2=q3+q4Dtwice the total flux through S due to q3andq4ifq1+q2=q3+q4. - Question 2 - Select One
The value of charge q1,q2andq3 as shown in the figure are
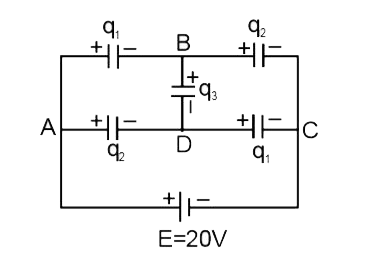 Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC
Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC - Question 3 - Select One
The electric flux through a closed surface area S enclosing charge Q is ϕ If the surface area is doubled, then the flux is
A2ϕBϕ/2Cϕ/4Dϕ
A conducting sphere S1 intersects a closed surface S2 as shown in the figure.A positive charge q is placed at a point P .What is the value of electric flux through the surface S2 ? q P
View SolutionShow three points charges +2q. -q and +3q, Two charges +2q and -q are enclosed within a surface 'S' What is the electric flux due to this configuration through the surface 'S' ?
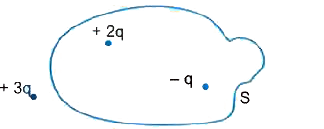 View Solution
View SolutionThree charges −q1, +q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
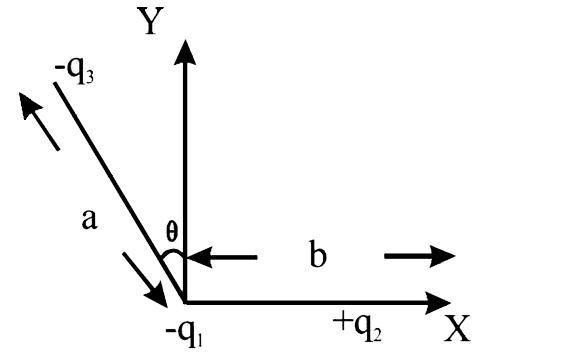 View Solution
View SolutionThree point charges are placed as shown in the figure. S is a gaussian surface ϕ is the net flux passing through surface A and E be the electric field at point P on the surface, then
 View Solution
View SolutionIn the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
 View Solution
View Solution

