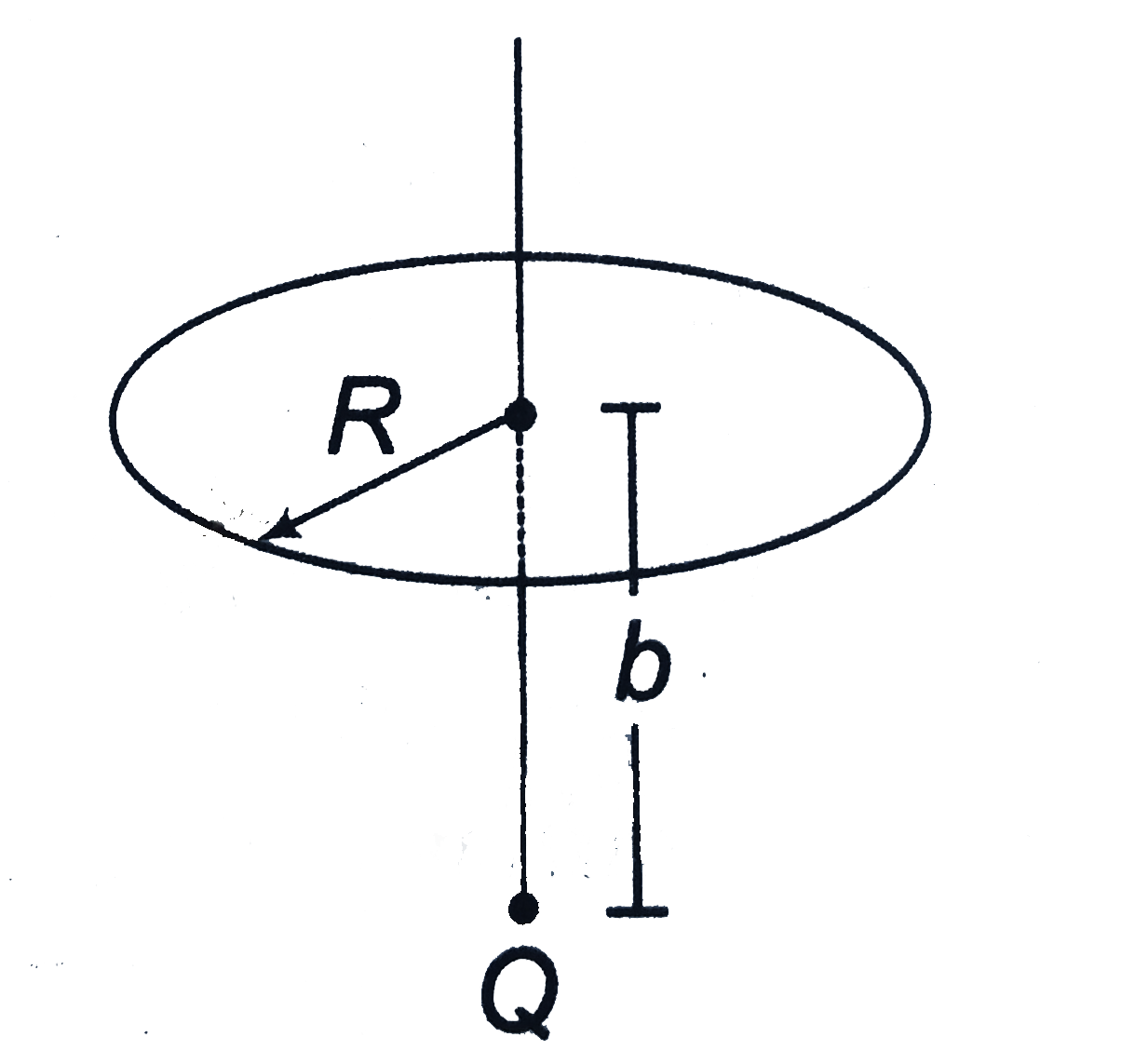
A point charge Q is located on the axis of a disk of radius R at a distance b from the plane of the disk. Show that if one-fourth of the electric flux from the charge passes through the disk, then R=√3b.

The correct Answer is:√3b
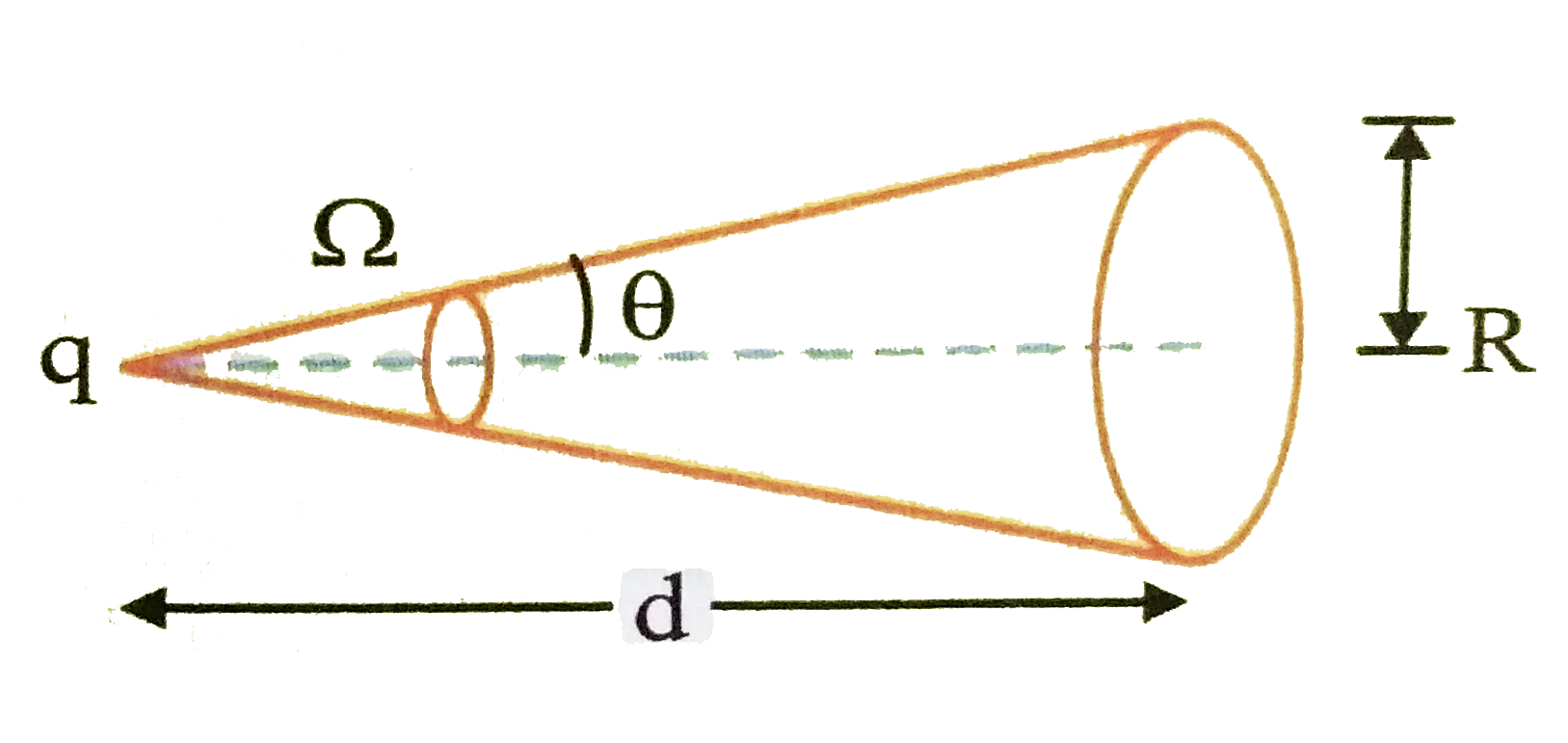
Solid angle subtended by disk at Q is
Ω=2π(1−cosα)
=2π[1−b√b2+R2]
Flux through disk is (QΩ)/(ε04π)
It is given to be Q/4ε0.
So, Q4ε0=QΩε04π
Solve to get R =√3b.

Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Single Correct
40 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct
8 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.2
14 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
Similar Questions
A point charge Q is located on the axis of a disc of radius R at a distance b from the plane of the disc (figure). Show that if one-fourth of the electric flux from the charge passes through the disc, then R=√3b.
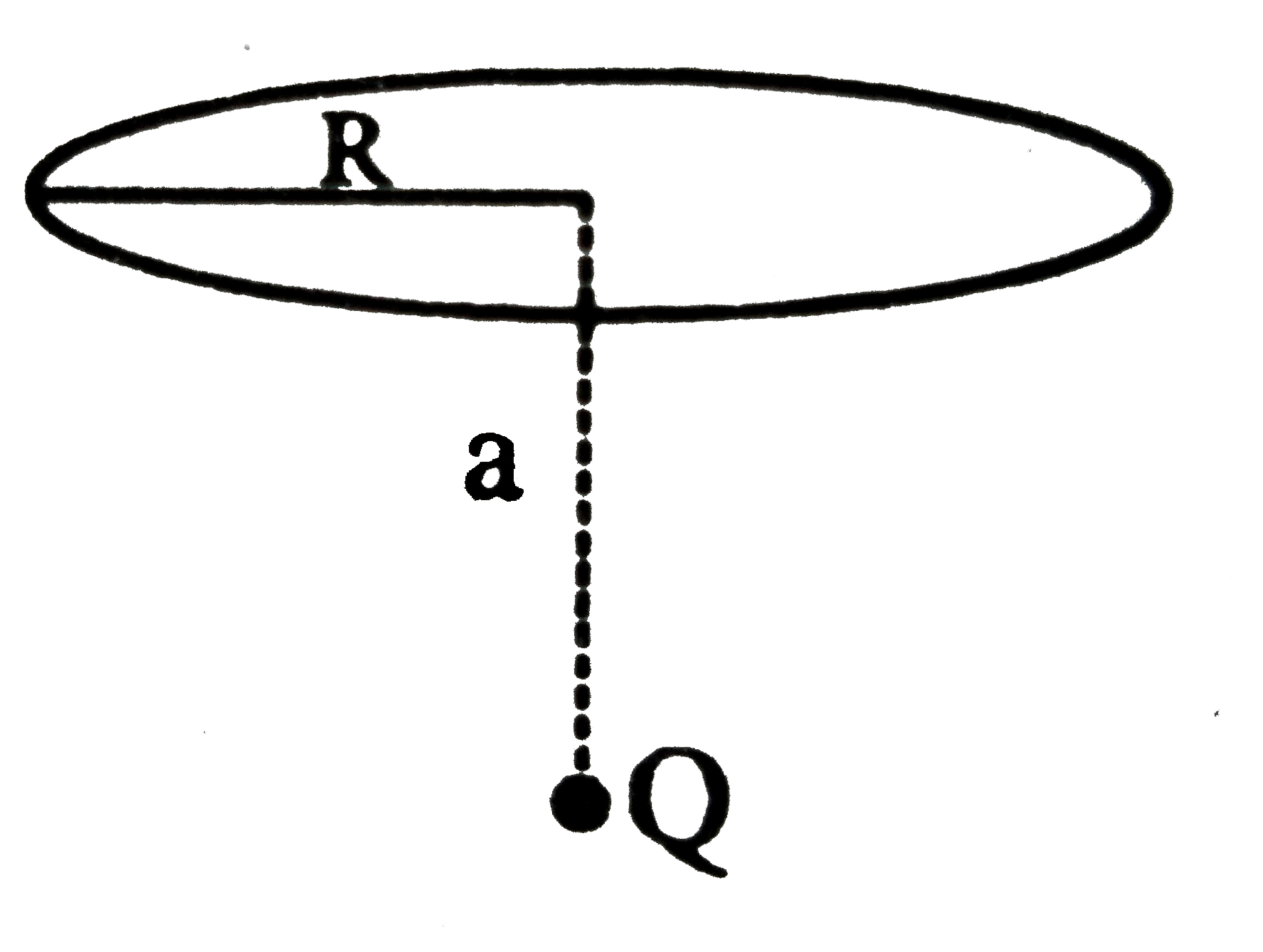
View SolutionA point charge Q is located on the axis of disc of a radius R at a distance a from the plane of the disc . If one fourth (1/4th) of the flus from the charge passes through the disc, then find the relation between a &R.
 .
.
View Solution
Knowledge Check
A point charge q is placed at a point on the axis of a non-conducting circular plate of radius r at a distance R(>>r) from its center. The electric flux associated with the plate is
Aqr24πε0R2Bqr24ε0R2CqR24ε0r2Dq4ε0A circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
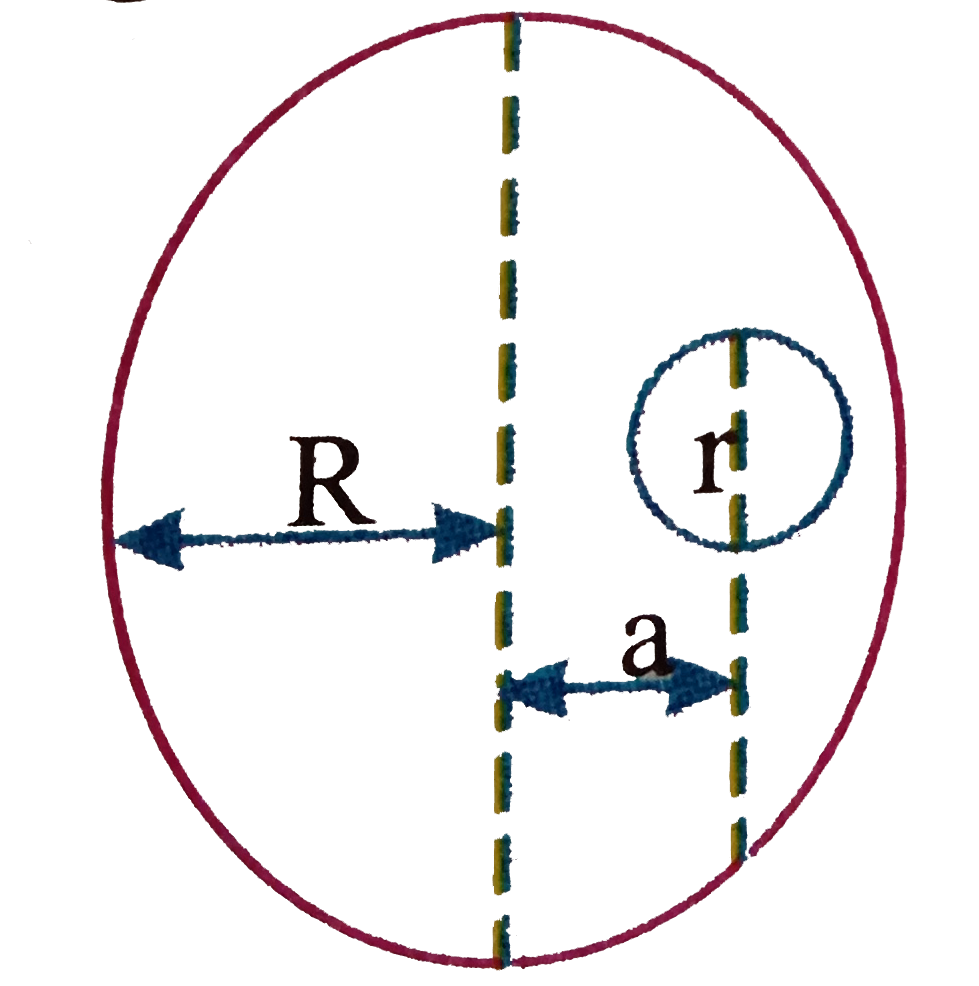 AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2
AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2An infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surfance of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surfce is .
 AπR2σɛ0Bπ(R−x)2σɛ0Cπ(R−x)2σɛ0Dπ(R2−x2)σɛ0
AπR2σɛ0Bπ(R−x)2σɛ0Cπ(R−x)2σɛ0Dπ(R2−x2)σɛ0
A point charge q is located on the axis of a disc of radius R at a distance b from the plane of the disc as shown in figure 1.295 What should be the radius of the disc if one fourth of the total electric flux form the charge passes through the disc.

View SolutionPotential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View SolutionA point charge Q is placed at the centre of circular disc of radius r . Calculate the electric flux associated with circular disc.
View SolutionA point charge q is placed at a distance d form the center of circular disc of radius R. Find electric flux through the disc due to that charge
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View Solution
