Consider Gauss's law
Then, for the situation shown in figure at the Gaussian surface
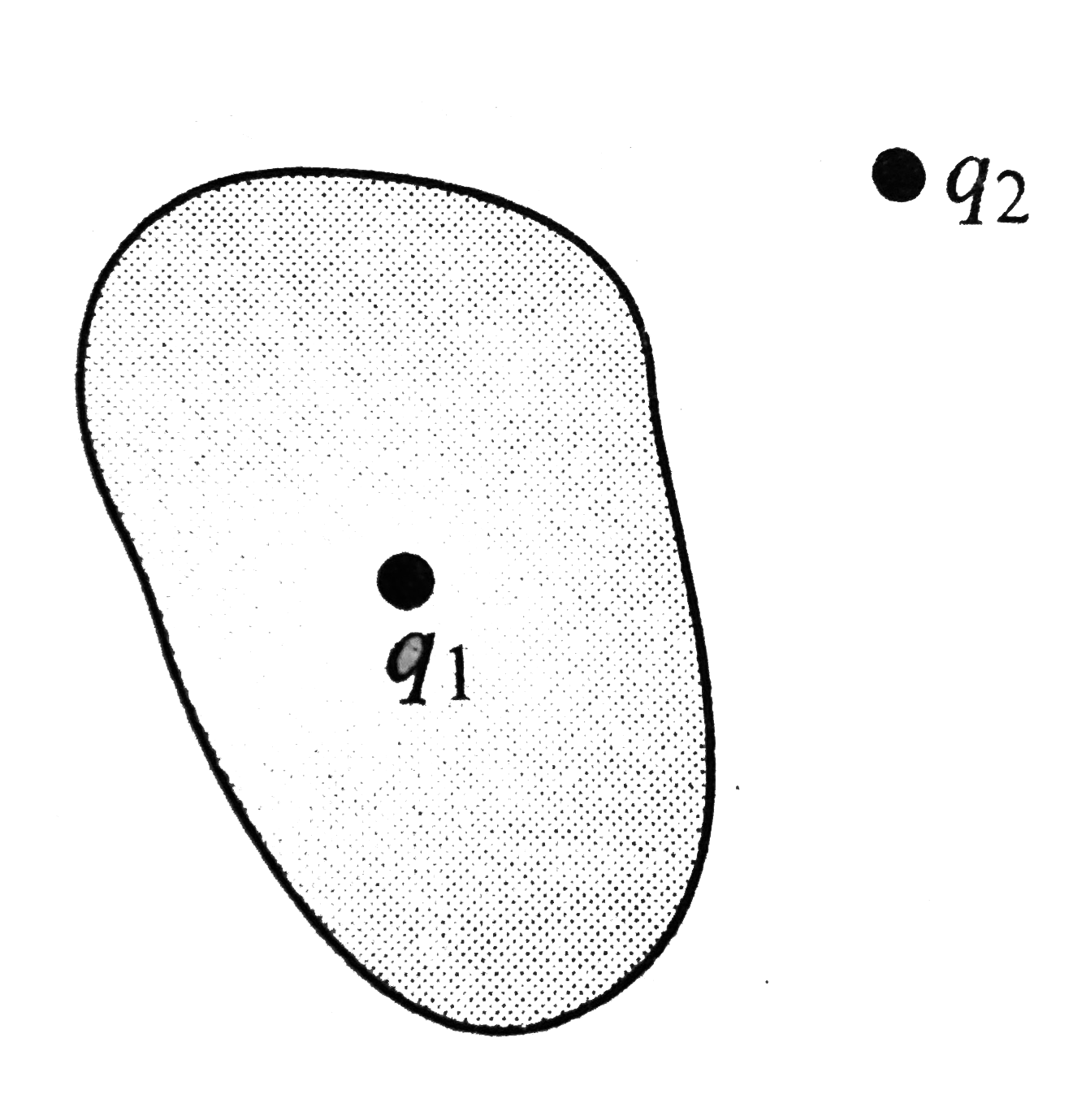
A
would be zero.
B
due to both would not be zero
C
due to both would not be zero.
D
due to would be zero.
Video Solution
Text Solution
The correct Answer is:B, D
In of Gauss's law , is due to all point charges present in space and depends only on the enclosed charges.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension36videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type7videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Single Correct40videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.514videos
ELECTRIC POTENTIAL
Similar Questions
Knowledge Check
- Question 1 - Select One
Consider the situation shown in the figure.
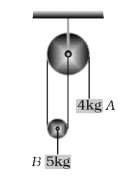
Find acceleration of A.A2g7Bg7C3g7D2g5 - Question 2 - Select One
Consider the situation shown in the figure.
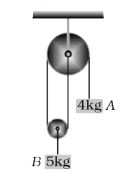
Find acceleration of B.Ag7B2g7C3g7D2g5 - Question 3 - Select One or More
For the situation shown in the figure, select the correct statements (s).
 APotential of the conductor is q/4πε0(d+R)BPotential of the conductor is q/4πε0dCPotential of the conductor cannot be determined as nature of distribution of induced charges is not known.DPotential at point B due to induced charges is −qR/4πε0(d+R)d
APotential of the conductor is q/4πε0(d+R)BPotential of the conductor is q/4πε0dCPotential of the conductor cannot be determined as nature of distribution of induced charges is not known.DPotential at point B due to induced charges is −qR/4πε0(d+R)d
For the situation shown in the figure below, mark out the correct statement(s) :
 View Solution
View SolutionConsider the situation as shown in the figure. Find TminTmax.
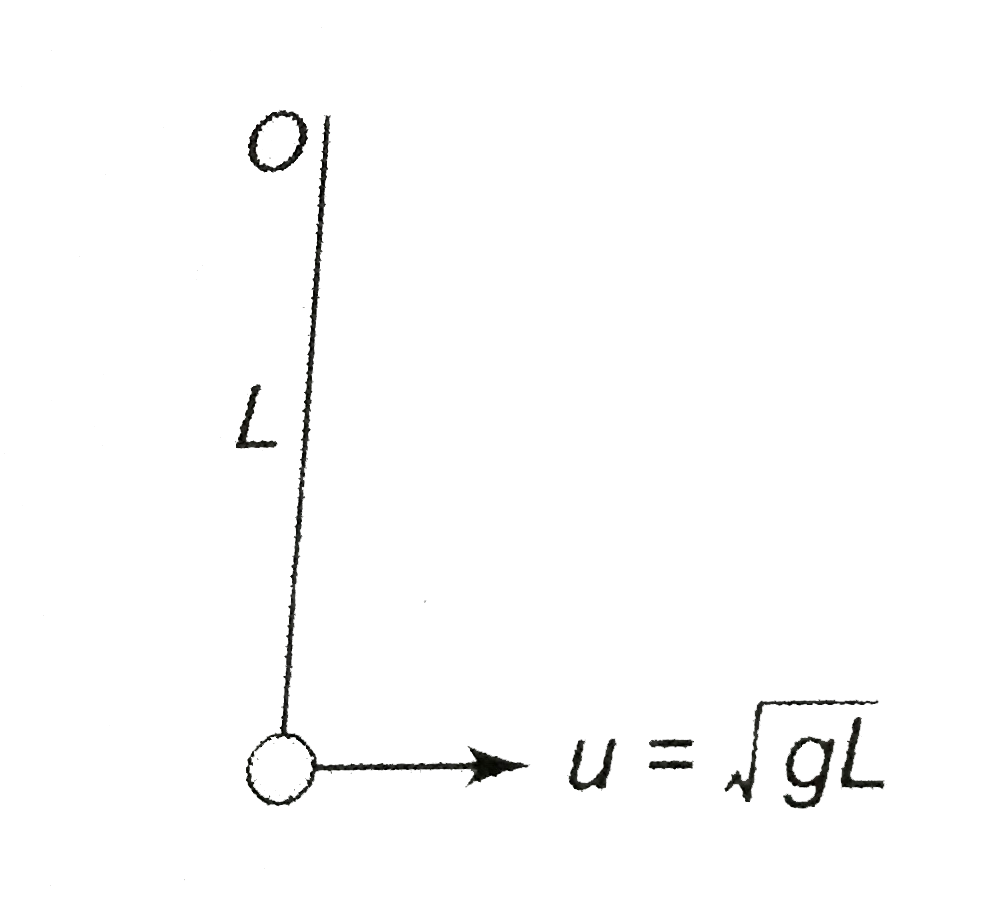 View Solution
View SolutionConsider the situation shown in the given below. What are the sign of q1andq2 ?
View SolutionConsider the situation as shown in the figure. Choose the correct option.
 View Solution
View SolutionIn Gauss' s theorem ∮sEds=qε0 The surface integral is evaluated by choosing a closed surface called the Gaussian surface. Here
View Solution



