A uniform field of magnitude →E=2000NC−1 is directed θ=37∘ below the horizontal [fig. 3.11].
![A uniform field of magnitude vec E = 2000 NC^-1 is directed theta = 37^(@) below the horizontal [fig. 3.11]. . (i) Find the potential difference between P and R. (ii) If we define the reference level of potential so that potential at R is VR = 500 V, what is the potential at P?](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V03_C03_S01_009_Q01.png) .
.
(i) Find the potential difference between P and R.
(ii) If we define the reference level of potential so that potential at R is VR=500V, what is the potential at P?
(i) Here E=2000NC−1,θ=37∘,VR=500V
Δl=PR=5cm=5×10−2m
VR−VP=→E.Δ→l=−Edlcosθ
=−(2000NC−1)(5×10−2m)cos37∘
VR−VP=−80V
Thus, VP−VR=→E.Δ→l=80V
(ii) As VP−VR=80VandVR=500V,
VP=500V+80V=580V.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Knowledge Check
If the potential difference between A and D is V, what will be potential difference between F and C. each of the resistance is R.
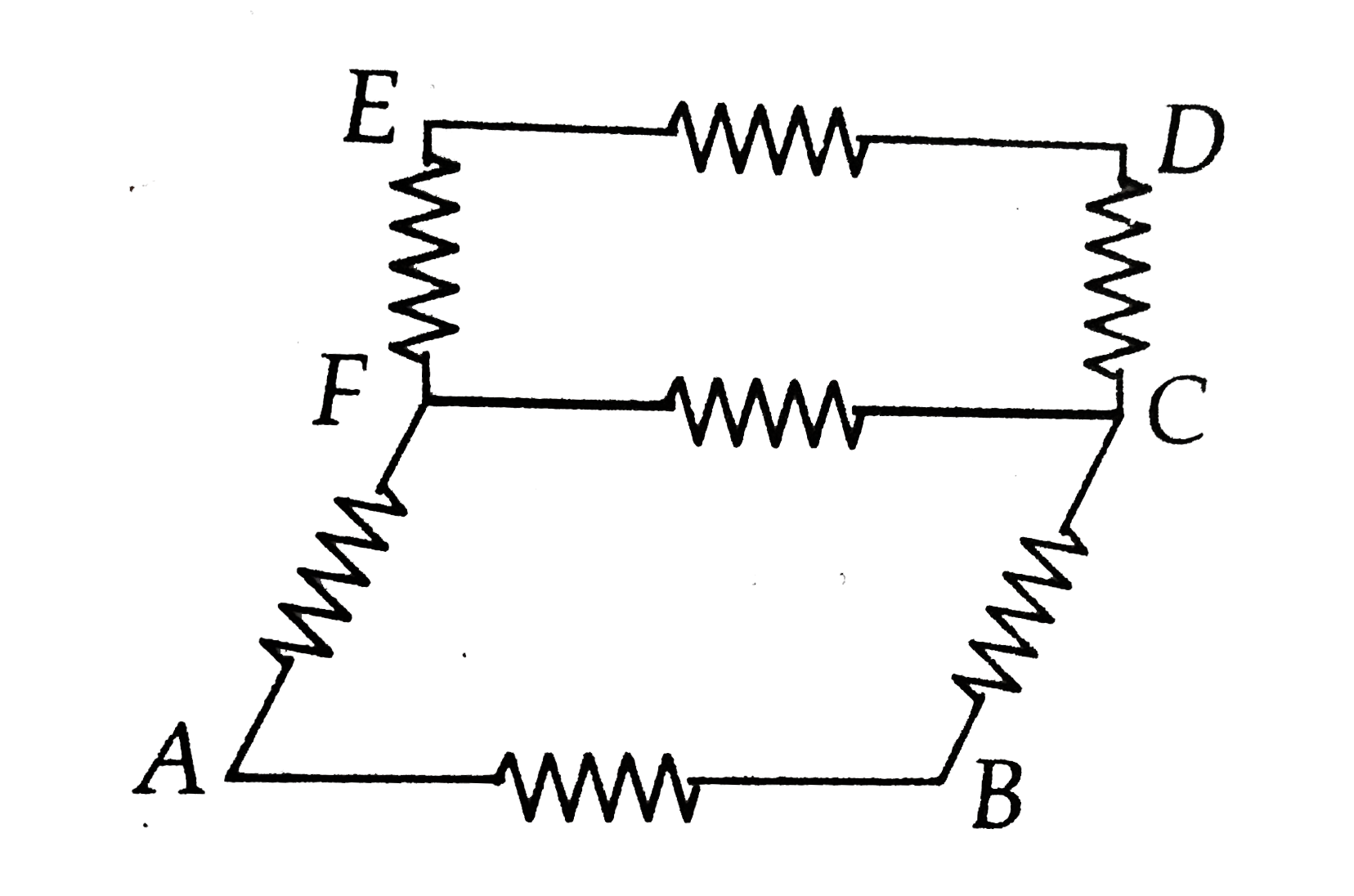 AV/3BV/4CV/6DV/8
AV/3BV/4CV/6DV/8Uniform electric field of magnitude 100V/m in space is directed along the line y=3+x. Find the potential difference between point A(3,1) & B(1,3)
A100VB200√2VC200VD0The r.m.s. value of potential difference V shown in Fig. is
 AV0BV0/2CV0/√2DV0/√3
AV0BV0/2CV0/√2DV0/√3
In the circuit shown in Fig. (i) find the phase difference between the currents through L and R1
(ii) find the phase difference between potential differece across C and R2
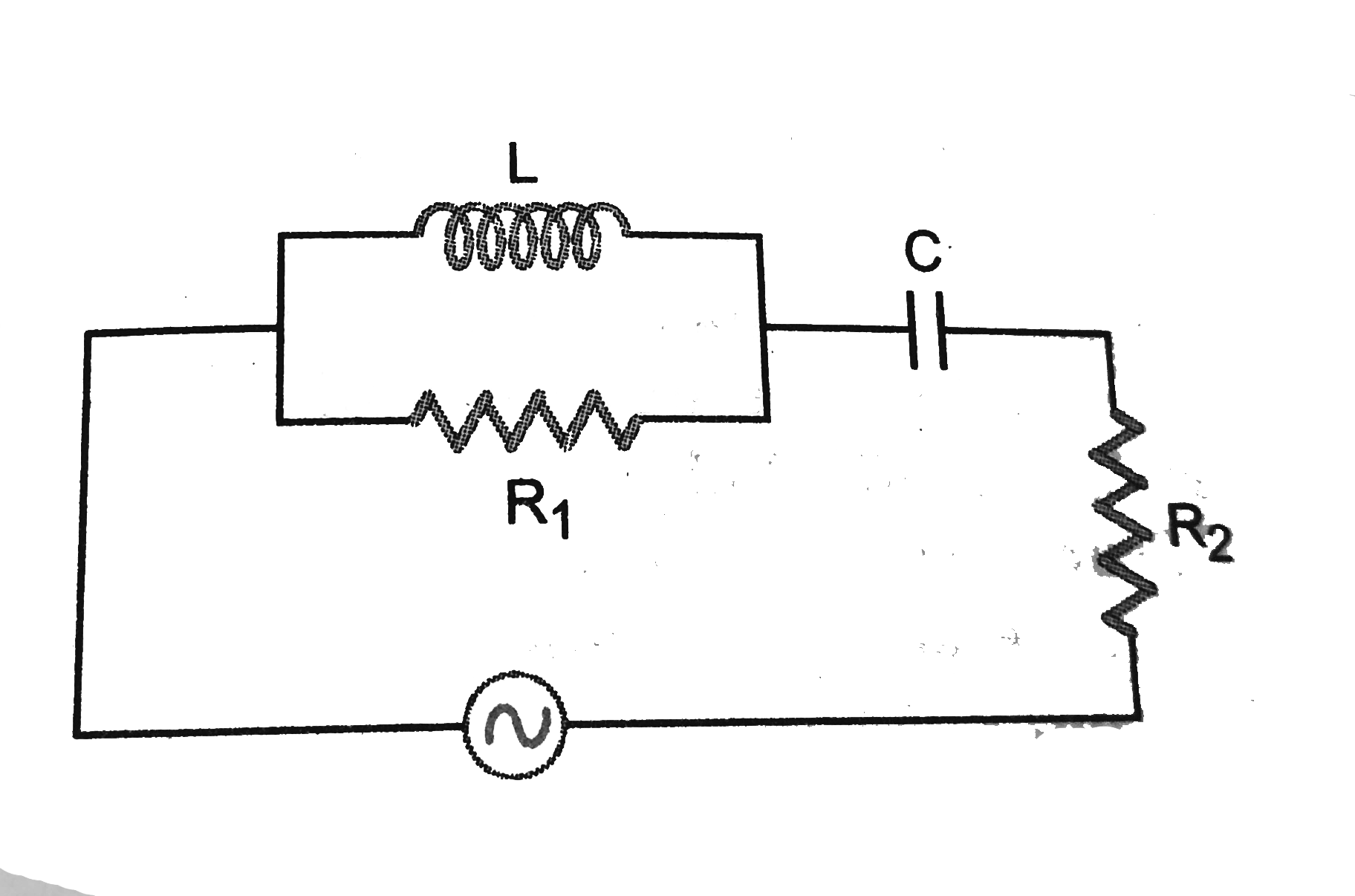
View SolutionIf the circuit a potential difference of 3V is required between the point CandD. Find the value of resistance r2
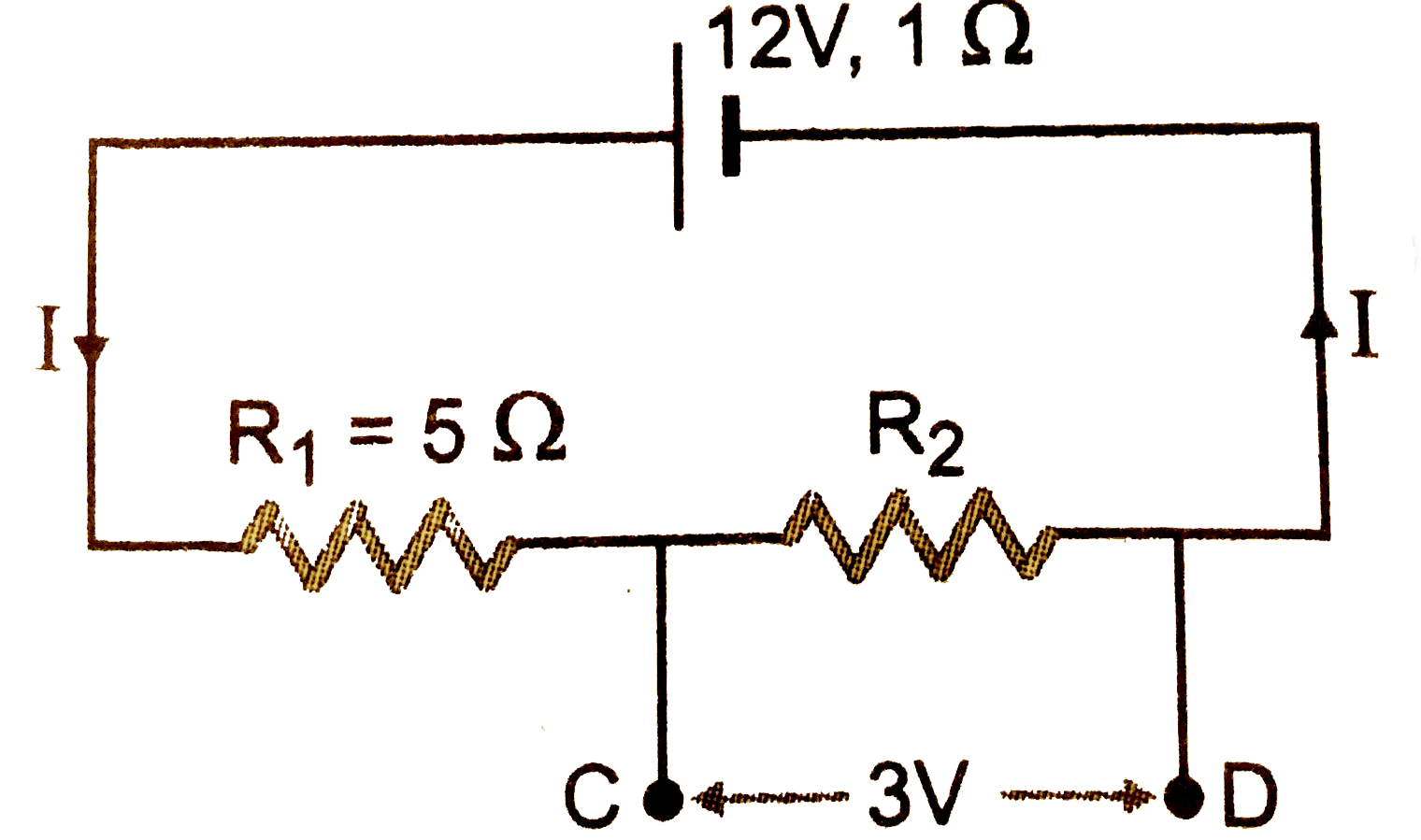
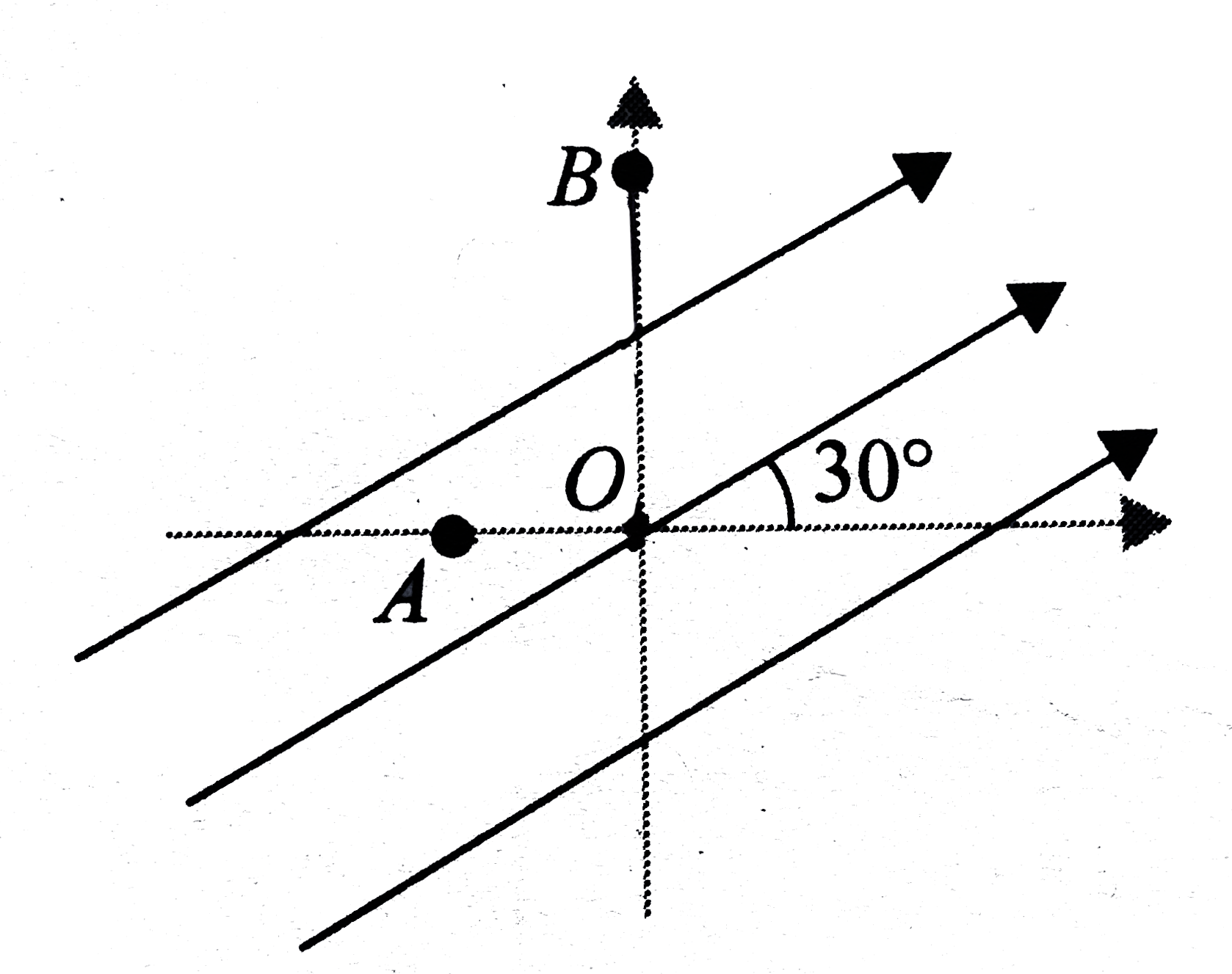
View SolutionA uniform electric field of 100Vm−1 is directed at 30∘ with the positive x - axis as shown in (Fig. 3.153). OA=2m and OB=4m.
 .
.
The potential difference VB−VA is.
View SolutionA uniform electric field of 100Vm−1 is directed at 30∘ with the positive x - axis as shown in (Fig. 3.153). OA=2m and OB=4m.
 .
.
The potential difference VO−VA is.
View SolutionLet gravitation field in a space be given as E=−(k/r) If the reference point is a distance d where potential is V1 then relation for potential is .
View Solution