Two capacitors C1 and C2 are charged separately to potentials 20Vand10V, respectively. The terminals of capacitors C1andC2 are marked as (A-B) and (C-D), respectively. A is connected with CandB is connected with D.
i. Find the final potential difference across each capacitors.
ii. Find the final charge in both capacitors
iii. How much heat is produced in the circuit.
128μC 142μC 60uJ
28μC 42μC 60uJ
28μC 42μC 160uJ
2.8μC 4.2μC 60uJ
The correct Answer is:B
To solve the problem involving two capacitors C1 and C2 charged to different potentials and then connected, we will follow these steps:
Step 1: Understand the Initial Conditions
- Capacitor C1 is charged to 20V.
- Capacitor C2 is charged to 10V.
- The capacitors are connected such that terminal A of C1 is connected to terminal C of C2, and terminal B of C1 is connected to terminal D of C2.
Step 2: Calculate the Equivalent Capacitance
When the capacitors are connected in parallel, the equivalent capacitance Ceq is given by:
Ceq=C1+C2
However, we need to find the final potential difference across each capacitor, which requires us to consider the charge on each capacitor.
Step 3: Calculate Initial Charges
The initial charge on each capacitor can be calculated using the formula:
Q=C⋅V
Let Q1 be the charge on C1 and Q2 be the charge on C2:
Q1=C1⋅20V
Q2=C2⋅10V
Step 4: Find the Final Voltage Across Each Capacitor
When the capacitors are connected, they will share the total charge. The final voltage Vf across both capacitors can be found using the conservation of charge:
Qtotal=Q1+Q2
The final voltage across both capacitors will be the same:
Vf=QtotalCeq
Step 5: Calculate Final Charges
The final charge on each capacitor can be calculated using:
Qfinal=C⋅Vf
Thus, for each capacitor:
Q1,final=C1⋅Vf
Q2,final=C2⋅Vf
Step 6: Calculate Heat Produced
The heat produced in the circuit can be calculated from the energy stored in the capacitors before and after they are connected. The energy stored in a capacitor is given by:
U=12CV2
Calculate the initial energy Uinitial and the final energy Ufinal:
Uinitial=12C1(202)+12C2(102)
Ufinal=12C1V2f+12C2V2f
The heat produced Qheat is:
Qheat=Uinitial−Ufinal
Final Answers
1. Final potential difference across each capacitor: Vf (calculated from the above steps).
2. Final charge in both capacitors: Q1,final and Q2,final (calculated from the above steps).
3. Heat produced in the circuit: Qheat (calculated from the above steps).
- Capacitor C1 is charged to 20V.
- Capacitor C2 is charged to 10V.
- The capacitors are connected such that terminal A of C1 is connected to terminal C of C2, and terminal B of C1 is connected to terminal D of C2.
When the capacitors are connected in parallel, the equivalent capacitance Ceq is given by:
Ceq=C1+C2
However, we need to find the final potential difference across each capacitor, which requires us to consider the charge on each capacitor.
The initial charge on each capacitor can be calculated using the formula:
Q=C⋅V
Let Q1 be the charge on C1 and Q2 be the charge on C2:
Q1=C1⋅20V
Q2=C2⋅10V
When the capacitors are connected, they will share the total charge. The final voltage Vf across both capacitors can be found using the conservation of charge:
Qtotal=Q1+Q2
The final voltage across both capacitors will be the same:
Vf=QtotalCeq
The final charge on each capacitor can be calculated using:
Qfinal=C⋅Vf
Thus, for each capacitor:
Q1,final=C1⋅Vf
Q2,final=C2⋅Vf
The heat produced in the circuit can be calculated from the energy stored in the capacitors before and after they are connected. The energy stored in a capacitor is given by:
U=12CV2
Calculate the initial energy Uinitial and the final energy Ufinal:
Uinitial=12C1(202)+12C2(102)
Ufinal=12C1V2f+12C2V2f
The heat produced Qheat is:
Qheat=Uinitial−Ufinal
1. Final potential difference across each capacitor: Vf (calculated from the above steps).
2. Final charge in both capacitors: Q1,final and Q2,final (calculated from the above steps).
3. Heat produced in the circuit: Qheat (calculated from the above steps).
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Solved Examples10videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.113videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMSEXERCISE - QUESTION BANK40videos
ATOMS
- BOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
Similar Questions
If A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
View SolutionTwo capacitors of capacitances 3μFand6μF, are charged to potentials 2V and 5V respectively. These two charged capacitors are connected in series. Find the potential across each of the two capacitors now.
View Solution
Knowledge Check
- Question 1 - Select One
Two capacitors C1 and C2 are charged separately to potentials 20Vand10V, respectively. The terminals of capacitors C1andC2 are marked as (A-B) and (C-D), respectively. A is connected with CandB is connected with D.
i. Find the final potential difference across each capacitors.
ii. Find the final charge in both capacitors
iii. How much heat is produced in the circuit.A128μC 142μC 60uJB28μC 42μC 60uJC28μC 42μC 160uJD2.8μC 4.2μC 60uJ - Question 2 - Select One
Two capacitors having capacities C1andC2 are charged to voltages V1andV2 respectively. There will be no exchange of energy in connecting them in parallel, if
AC1=C2BC1V1=C2V2CV1=V2DC1V1C2V2 - Question 3 - Select One
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
Two capacitors of capacitances C1=6μFandC2=3μFare connected in series across a cell of emf 18 V. Calculate
(i) the equivalent capacitance,
(ii) the potential difference across each capacitor,
(iii) the charge on each capacitor.View SolutionTwo capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
View SolutionThree capacitors of capacitances 1μF,2μF, and 2μF, are cahrged up to the potential difference 30V,10V, and 15V, respectivly. If terminal A is connected with DC is connected with E and F is connected eith B, the find the charge flow in the ciruit and the final charge on the capacitors.
 . View Solution
. View SolutionIn the circuit shown the capacitors are C1=15μF,C2=10μFandC3=25μF. Find
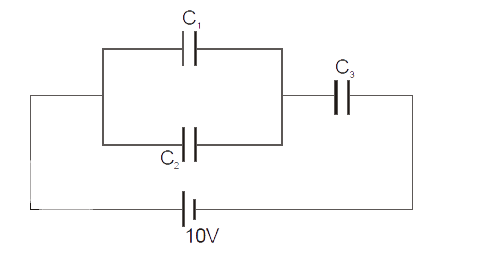
the potential difference across each capacitor.View SolutionA 10μF capacitor is charged to a potential difference of 1000V. The terminals of the charged capacitor are disconnected from the power supply and connected to the terminals of an uncharged 6μF capacitor. What is the final potential difference across each capacitor ?
View Solution

