Three capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emg6V. 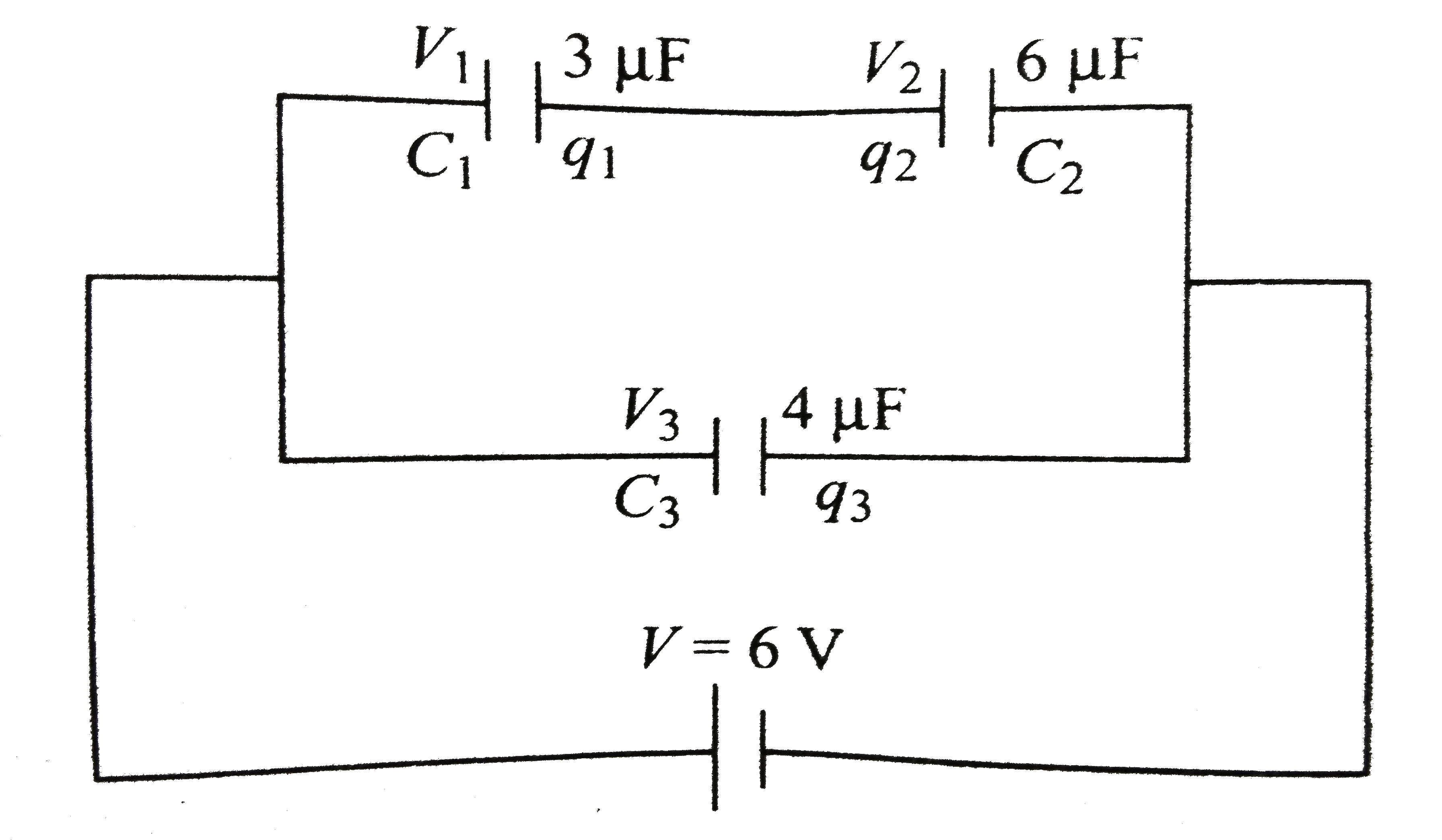 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.
i. C1 and C2 are in series, so their equivalent capacitance is
C=C1C2C1+C2=3×63+6=2μF
This C' will be in parallel C3,So<br>C_(eq)=C'+ C_(3)=2+4=6 muF<br>ii.6 Vwillbe∈paral≤lacrossC_(1)andC_(2)∈the∈verseratioofthe∩acitances.SopotentialdefferenceacrossC_(1)is<br>V_(1)=(C_(2)V)/(C_(1)+C_(2))=(6xx6)/(3+6)=4 V.<br>andpotentiald⇔ernceacrossC_(2)isV_(2)=(C_(1)V)/(C_(1)+C_(2))=(3xx6)/(3+6)=2 V<br>BecauseC_(3)isco∩ecteddirectlyarossthebaerywithoutanyother∩aci→r∈between,sopotentiald⇔erenceacrossC_(3)isV_(3) =V=6 V.Alsochar≥onC_(1)is<br>q_(1)=C_(1)V_(1)=3xx4=12 muC<br>andchar≥onC_(2)is<br>1q_(2)=C_(2)V_(2)=6xx2-12 muC<br>Weseetˆq_(1)q_(2),∵isseries,char≥isthesame.<br>chae≥onC_(3)is<br>q_(3)=C_(3)V_(3)=4xx6=24 muC.<br>A<ernativemethode→f∈dchar≥.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V03_C04_S01_016_S01.pngwh=80%mx-autosty≤=background:white;><br>Totalchar≥tˆwillflowthroughthebaeryis<br>Q = C_(eq)V = 6 xx 6 = 36 muC<br>Itwillbe÷d∫hedirectratioofC'andC_(3),so<br>q_(1) = (C'Q)/(C'+C_(3)) = (2 xx 36)/(2+4) = 12 muC<br>q_(3) = (C'Q)/(C'+C_(3)) = (4 xx 36)/(2+4) = 24 muC<br>E≠rgy∈C_(1)is<br>U_(1) = (1)/(2)C_(1)V_(1)^(2) = (1)/(2)xx3xx4 = 24mu J<br>E≠rgy∈C_(2)is<br>U_(2) = (1)/(2)C_(2)V_(2)^(2) = (1)/(2)xx6xx2^(2) = 12mu J<br>E≠rgyisC_(3)is<br>U_(3) = (1)/(2)C_(3)V_(3)^(2) = (1)/(2)xx4xx6 = 72mu J<br>Totale≠rgyis<br>U = U_(1) + U_(2) + U_(3) = 24 + 12 + 72 = 108 mu J<br>A<ernatively<br>U = (1)/(2) xx 6 xx 6^(2) = 108 muJ
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Solved Examples
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.1
13 Videos
- ATOMSBOOK - CENGAGE PHYSICSCHAPTER - ATOMSEXERCISE - QUESTION BANK
40 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
Similar Questions
Three capcitors of capacitances 4μF,
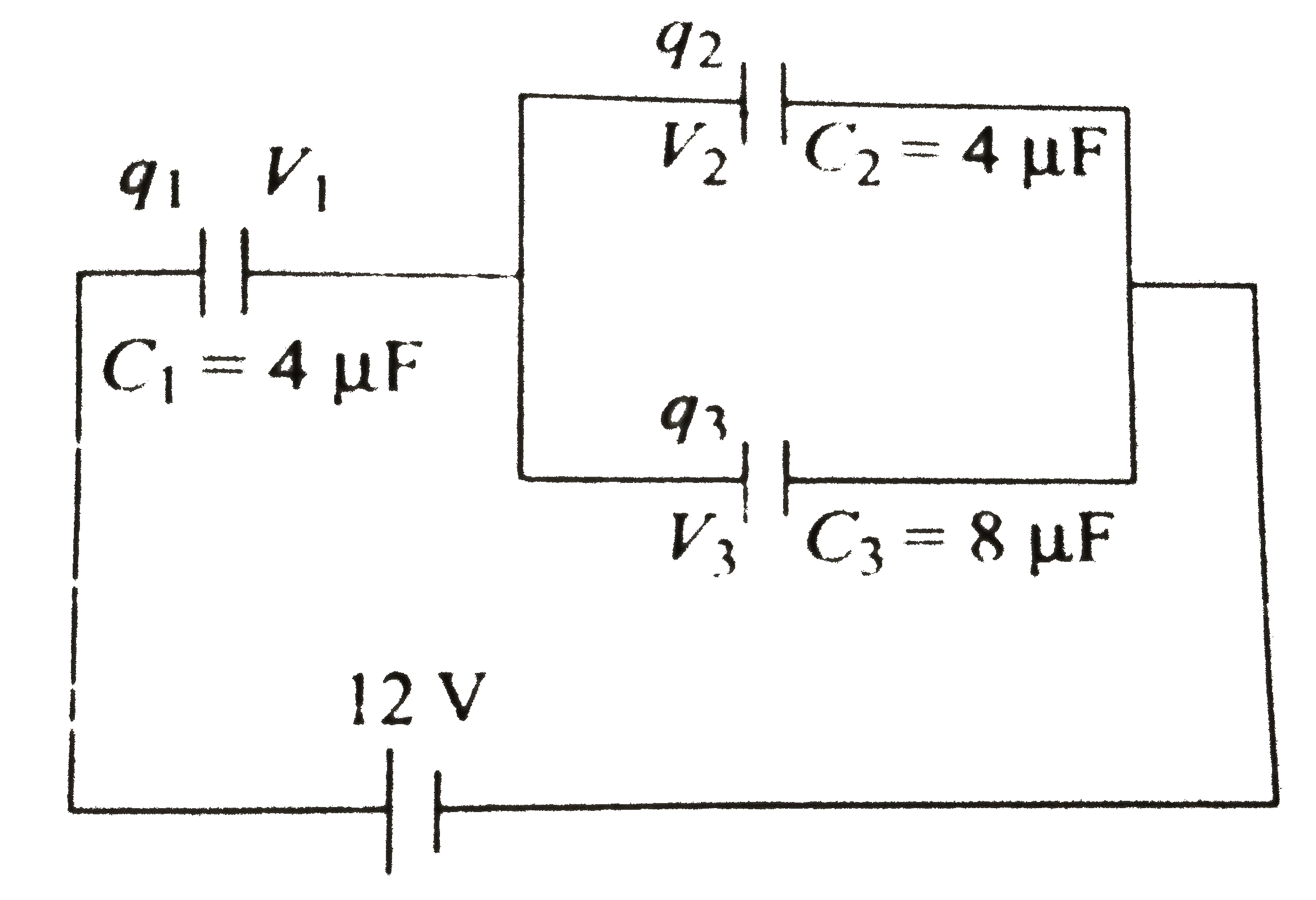 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.
View SolutionTwo capacitors of capacitances C1=6μFandC2=3μFare connected in series across a cell of emf 18 V. Calculate
(i) the equivalent capacitance,
(ii) the potential difference across each capacitor,
(iii) the charge on each capacitor.
View Solution
Knowledge Check
Three capacitors of capacitance 1μF,2μF and 3μF are connected in series and a potential difference of 11V is applied across the combination. Then, the potential difference across the plates of 1μF capacitor is
A2VB4VC1VD6VIf a 4μF capacitor is charged to 1 kV, then energy stored in the capacitor is
A1 JB4 JC6 JD2 JIn the circuit shown, the energy stored in 1μF capacitor is
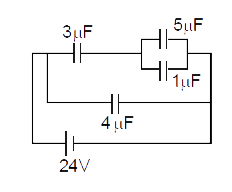 A40μJB64μJC32μJDnone of these
A40μJB64μJC32μJDnone of these
Two capacitors of capacitances 4μF and 6μF are connected in series with a battery of 20 V. find the energy supplied by the battery.
View SolutionThree capacitors of capacitances 2μF,2μFand4μF are connected across a battery of 10V as shown in the adjoining figure (g). Calculate the effective capacitance and charge on each capacitor.
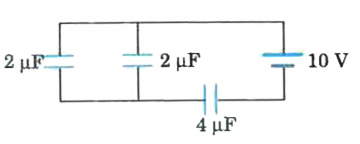
View SolutionThree capacitors of capacitances 2μF,2μFand4μF are connected to a battery of 10V as shown in the figure. Calculate the effective capacitance of the circuit and charge on each capacitor.
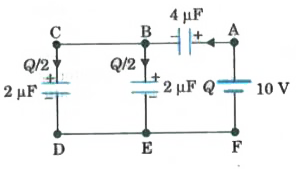
View SolutionFour capacitors of capacitances 2 μF and 1μF are connected across a battery of 10V as shown in the figure (q). Calculate the net capacitance of the combination and net charge across each capacitor.
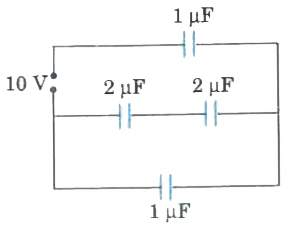
View SolutionIn the circuit shown in figure find

a. the equivalent capacitance
b. the charge stored in each capacitor and
c. the potential difference across each capacitor.
View Solution