A capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
Positive plate is given a charge Q, the charge distribution on different surface are shown in.
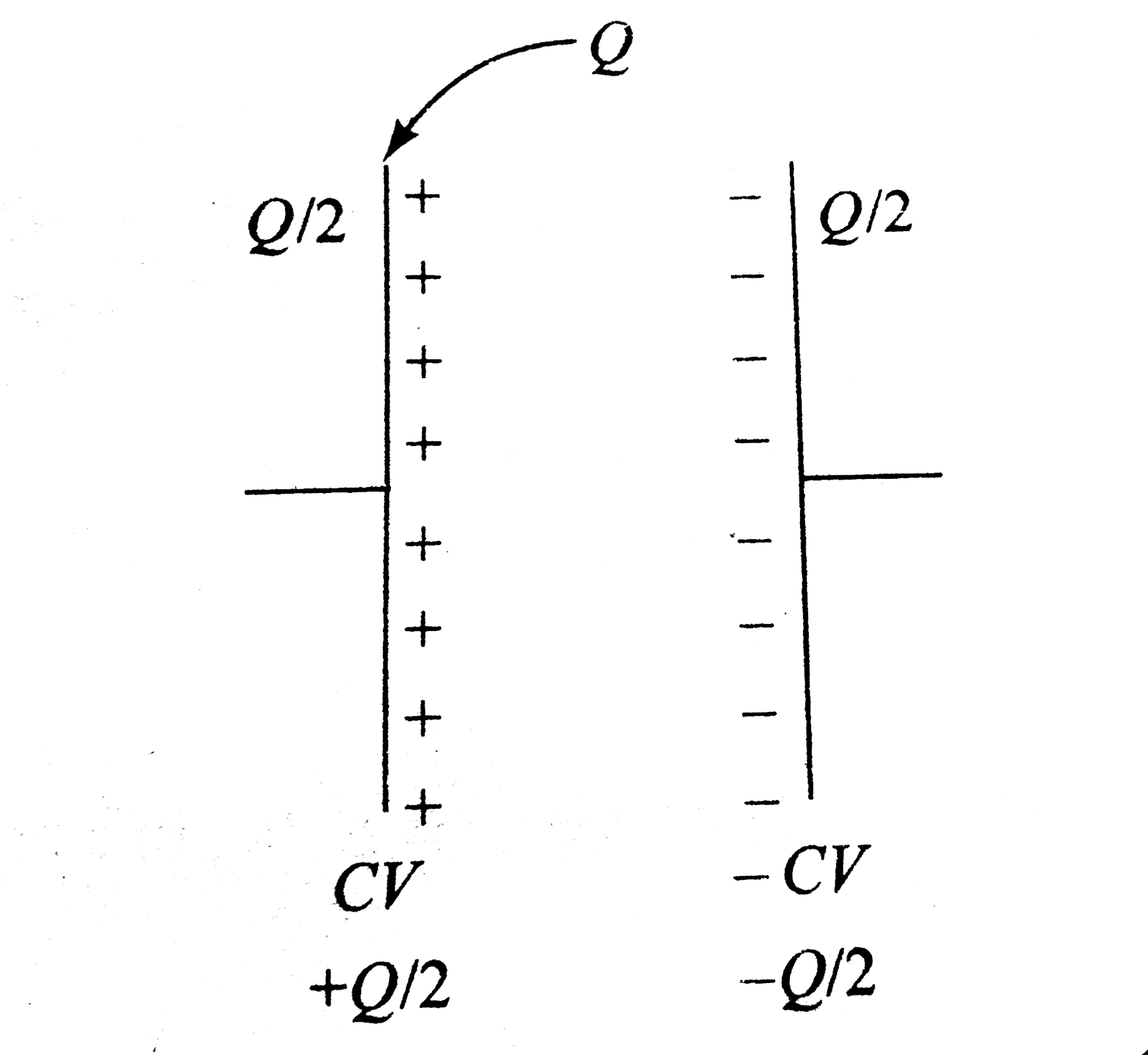 .
.
Hence new charge on capacitor is (CV+Q2) The potential difference between the plates will be.
V'=CV+Q2C=V+Q2C
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.232videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Subjective24videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Solved Examples10videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMSEXERCISE - QUESTION BANK40videos
ATOMS
- BOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
Similar Questions
Find charge on each capacitor and potential difference across each capacitor .
 View Solution
View SolutionA capacitor of capacitance 5 μF is charged to a potential difference of 10 volts and another capacitor of capacitance 9 μF is charged to a potential difference of 8 volts. Now these two capacitors are connected in such a manner that the positive plate of one is connected to the positive plate of other. Calculate the common potential difference across the two capacitors.
View Solution
Knowledge Check
- Question 1 - Select One or More
A capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then
 AEnergy stored in capacitor and inductor will be equal at time t=π2√LCBPotential difference across inductor will be V2 at time t=π3√LCCThe rate of increase of energy in magnetic field will be maximum at π4√LCDWhen the potentail difference across the capacitor √(3CL)
AEnergy stored in capacitor and inductor will be equal at time t=π2√LCBPotential difference across inductor will be V2 at time t=π3√LCCThe rate of increase of energy in magnetic field will be maximum at π4√LCDWhen the potentail difference across the capacitor √(3CL) - Question 2 - Select One
A capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
AC(V0−V)VBC(V−V0)VCCVV0DCV0V - Question 3 - Select One
A capacitor of capacitance 10μF is charged to a potential 50V with a battery. The battery is now disconnected and an additional charge 200μC is given to the positive plate of the capacitor. The potential difference across the capacitor will be.
A50 VB80 VC100 VD60 V
A 100pF capacitor is charged to a potential difference of 80.0V and the charging battery is disconnected. The capacitor is then connected in parallel with a second capacitor. If the potential difference across the first capacitor drops to 35.0 V what is the capacitance of this second capacitor?
View SolutionThe plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with to time. After 1s the potential difference between the plates is 39 V, then after 2s from the start, the potential difference (in V) between the plates is
View SolutionThe plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with to time. After 1s the potential difference between the plates is 39 V, then after 2s from the start, the potential difference (in V) between the plates is
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View Solution

