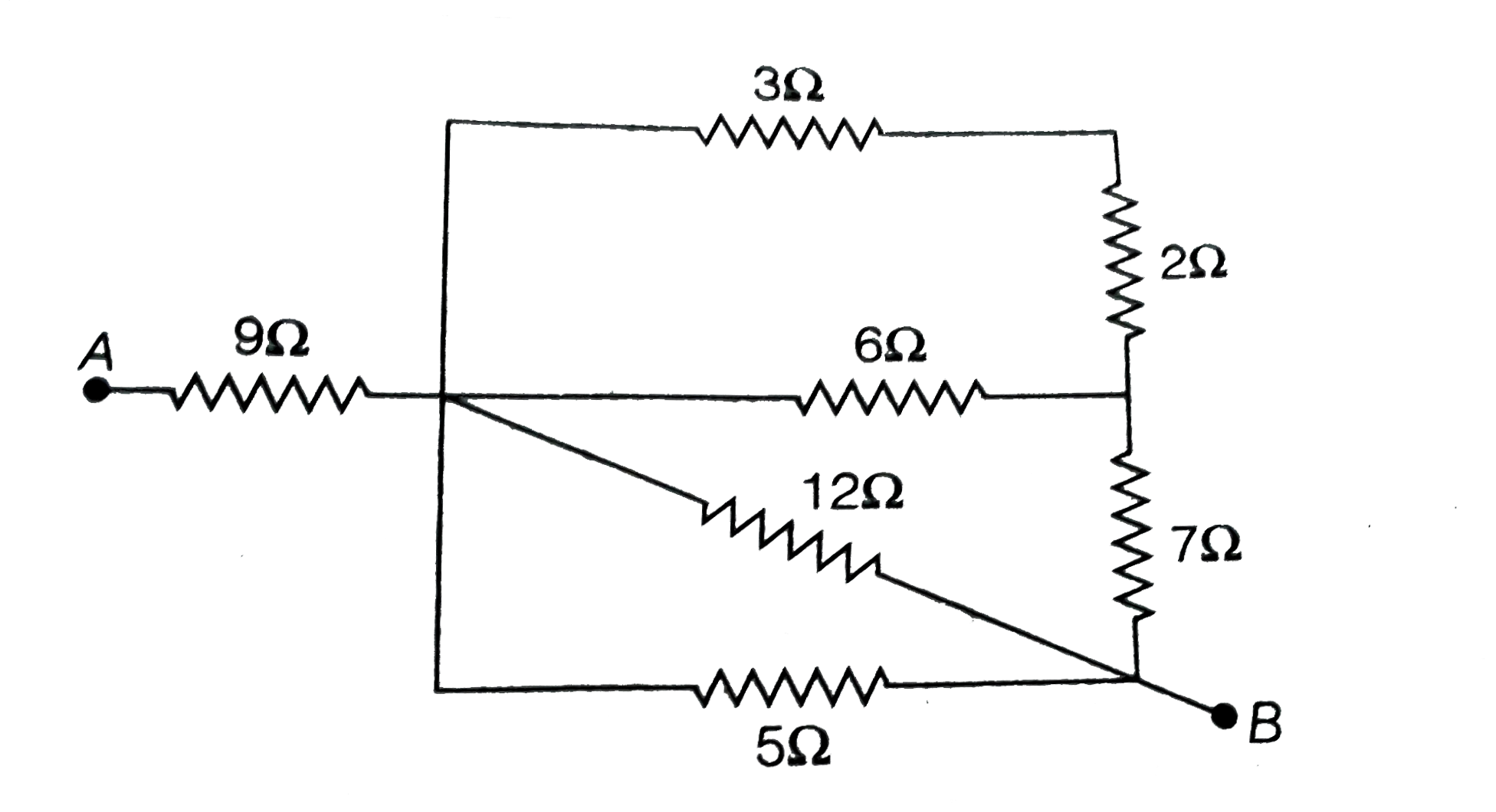
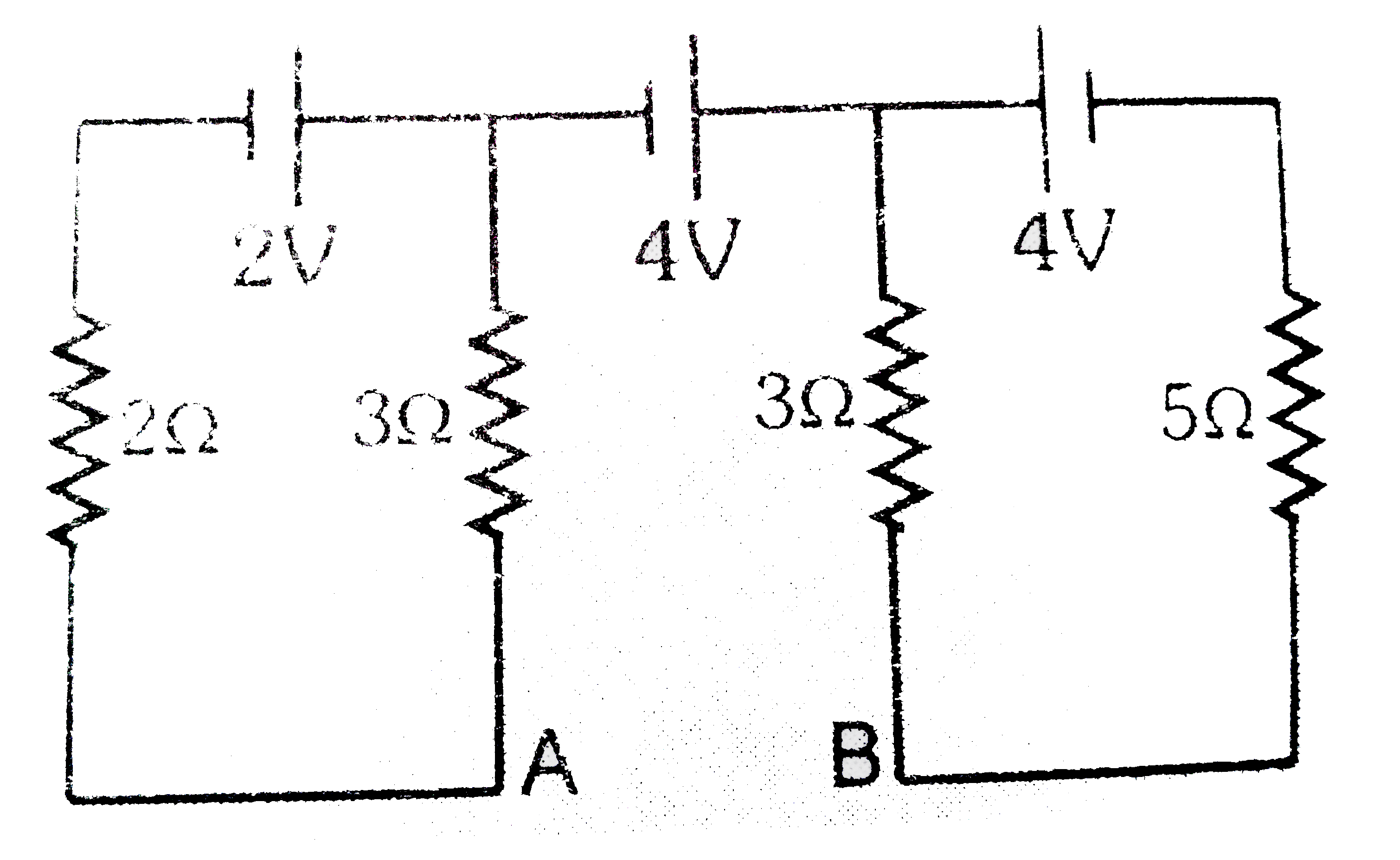In the given circuits calculate the resstance between points A and B.

Video Solution
Text Solution
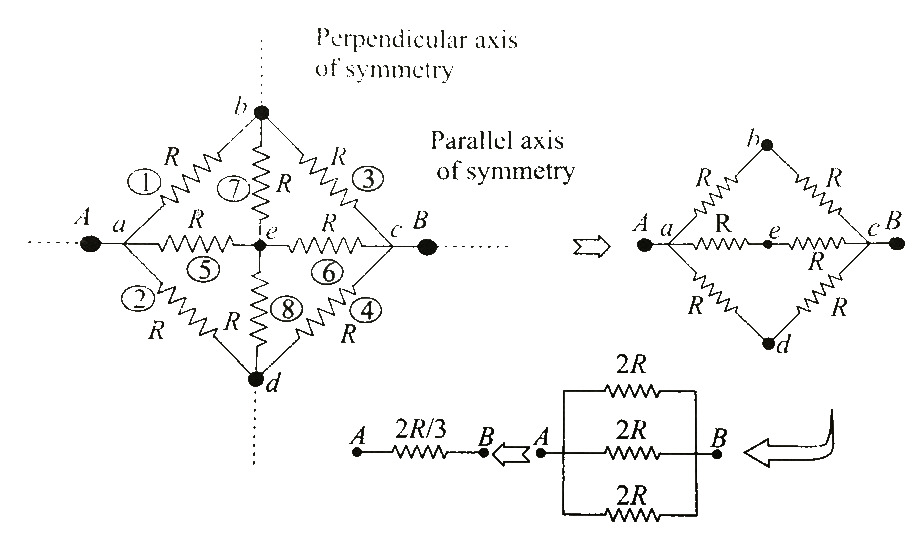
The circuit has both parallel axis and perpendicular
axis of symmetry (by symmetry we mean that the two parts
are mirror images of each other).
Method 1 : Let us solve this problem first usintg the perpendicular
axis of symmetry. We observe the following:
* The current in resistance (1) is equal to the current in resistance(3).
* The current in resistance (5) is equal to the current in resistance (6).
* The current in resistance (2) is equal to the current in
resistance(4).
From these observations it is clear that there is no mingling of
current form upper and lower branches into the middle branch.
Hence, resistor (7) and (8) are ineffective.
we also observe that all the points on the symmetry line are
equipotential. Hence, points b,e and d are equipotential points,
and so resistor (7) and (8) can be removed. The calculation of
effective resistance is shown if Fig. 5.28
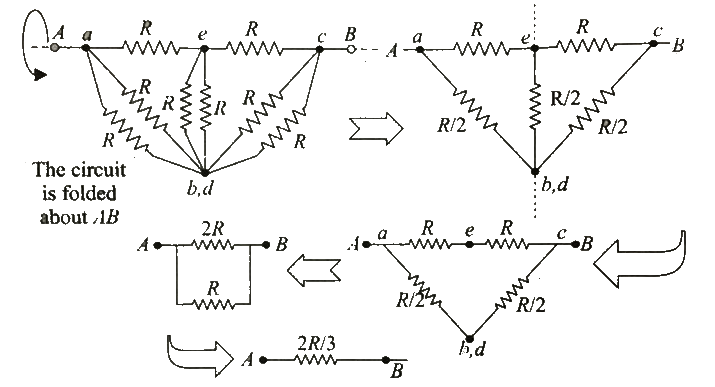
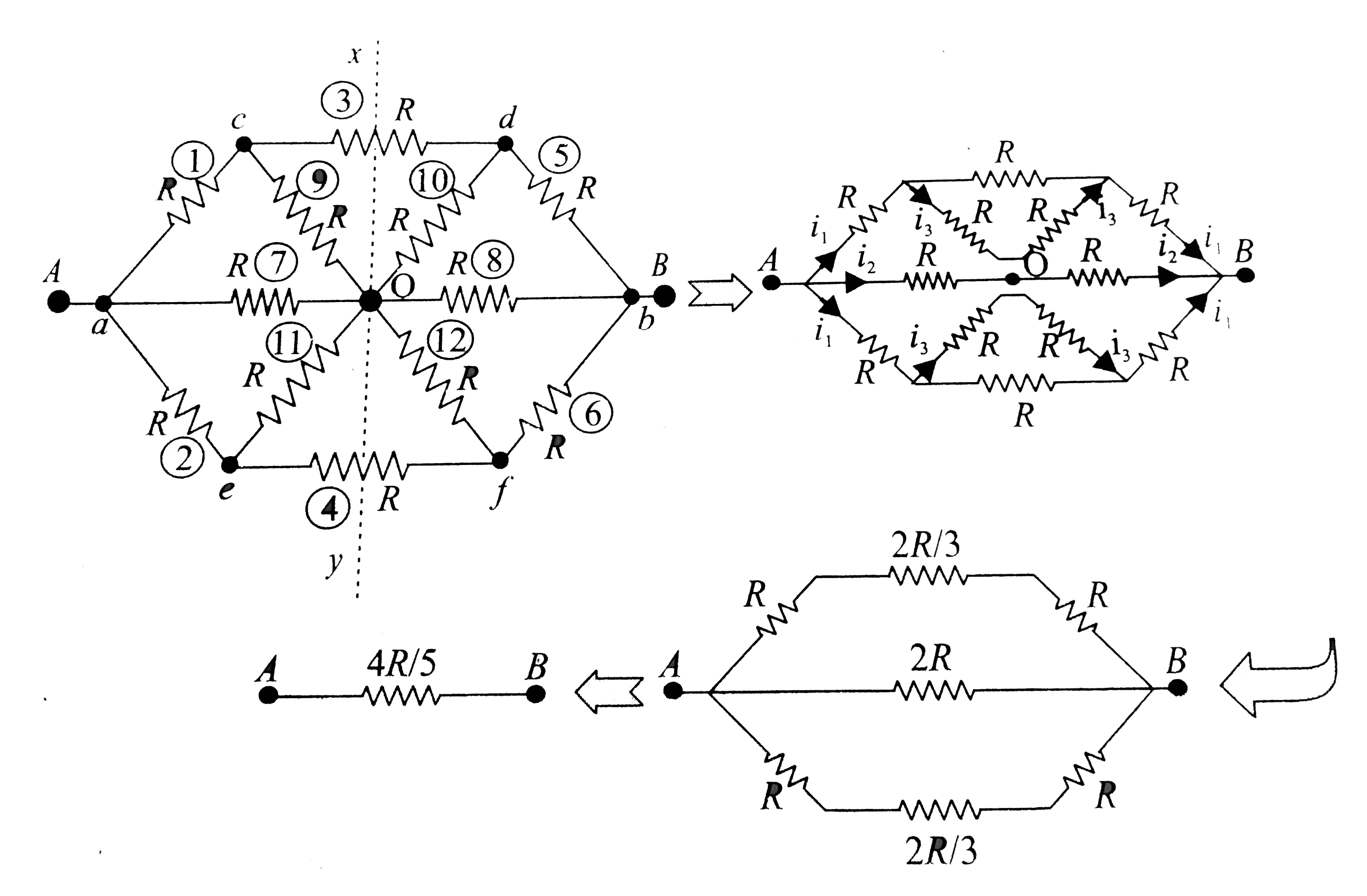
The current flow is not a mirror image in branches ab
and bc because the flow is in the same direction. This is called
asymmetric condition. The special thing about this asymmetry
is that current incoming at b is equal to the outgoing current.
A similar situation exists at b and d also. Thus, resistors in
branched be and de are ineffective.
Method 2: The circutit has parallel axis symmetry about the line ac, so the potential and current must also be symmetrical. Therefore. current in ab and ad are saem. Current in dc and bc are also same. Potentials of the points b,e, and d are same. The circuit can be folded about the parallel axis of symmetry. The calculation of equivalent resistance are shown in Fig.


(b) The current has parallel axis of symmetry about the line passing through a and b and perpendicular axis of symmetry about the line x-y.
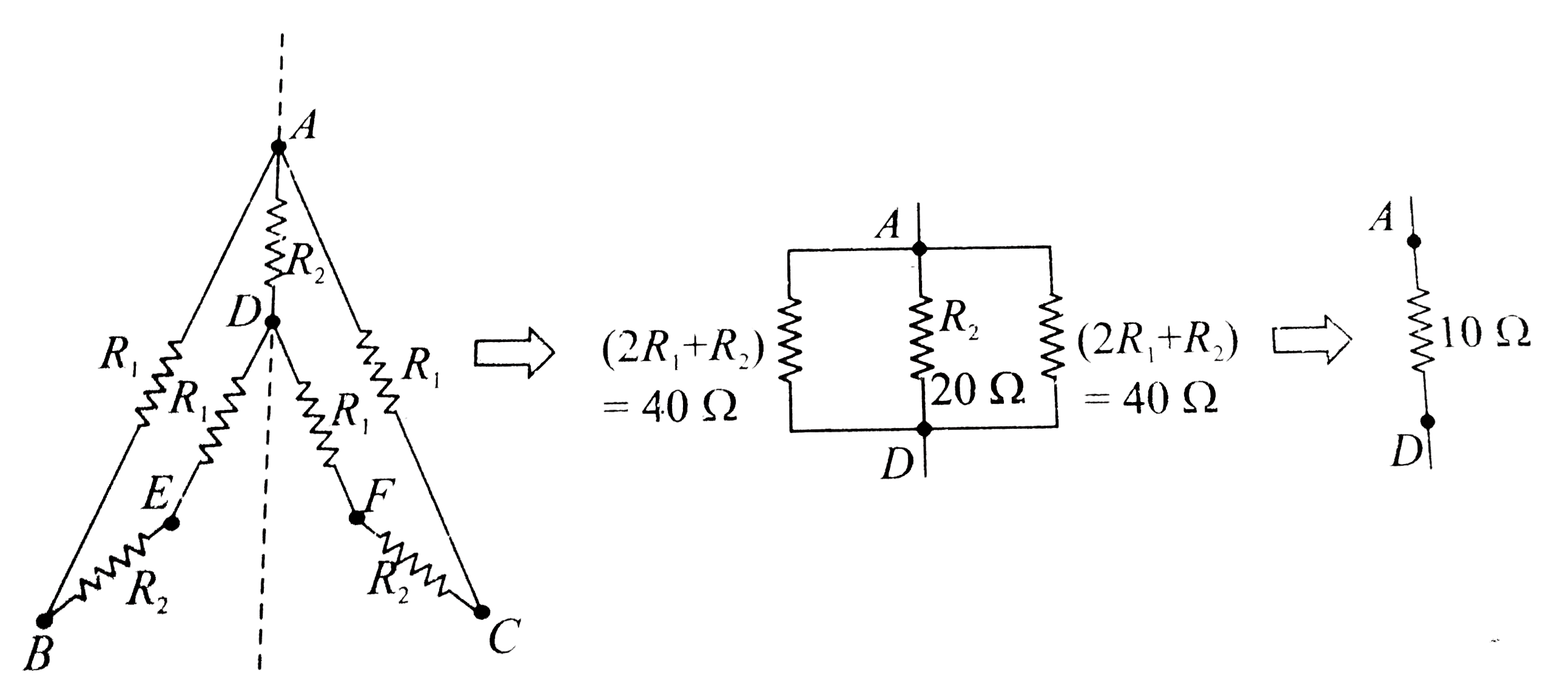
Method 1 : From perpnedicular axis of symmetry, it is clear that
*The current in resistane (7) is equal to the crrent in resistance (8).
*The current in resistane (9) is equal to the crrent in resistance (10).
*The current in resistane (11) is equal to the crrent in resistance (12).
From these observations, it is clear that there is no mingling of current from upper and lower branch into the middle branch. The upper and lower branches can be separted from the middle bracnh. The calculations of equivalent resistance are shown in fig. 5.60
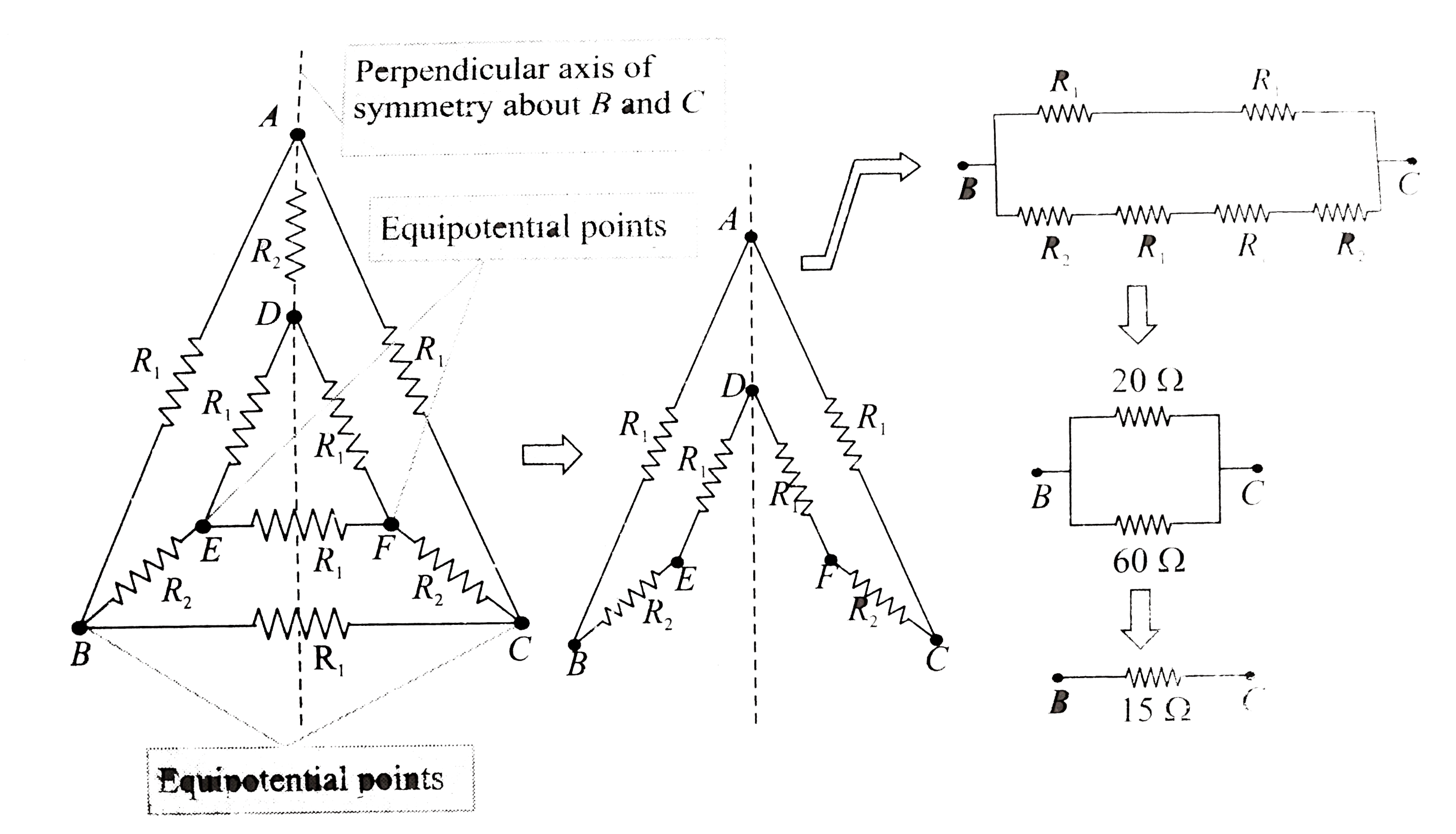
Method 2 : we can observe the parallel axis symmetry. The potentials of c and e and that of d and f shoudl be equal. Hence, the circuit can be folded about the line passing through A and B. The calculations of equivalent resistance are shown in Fig. 5.61. As shown in the figure, finally 2R and 4R/3 are in parallel. Hence, the equivalent resistance will be
Req=2R×4R310R3=4R5=4R5







|
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Solved Examples
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.1
Explore 28 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
Knowledge Check

In the given circuit calculate the potential difference points A and B.A12VB24VC36VD48VIn given circuit , the potential difference between points A and B is
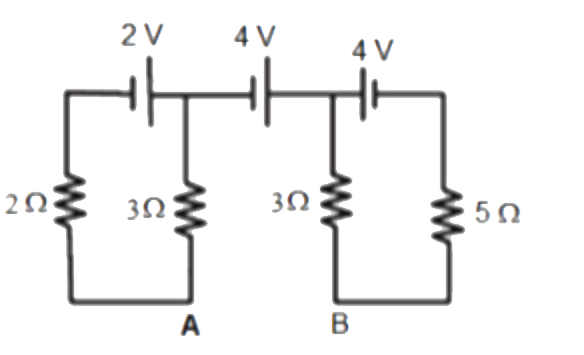 A10 VB15 VC20 VD5V
A10 VB15 VC20 VD5V
In the given circuit calculate potential difference between the points P and Que.
View SolutionIn the given circuit, the potential difference between the points A and B is
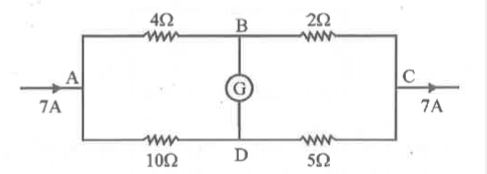
View SolutionConsider the following circuit:
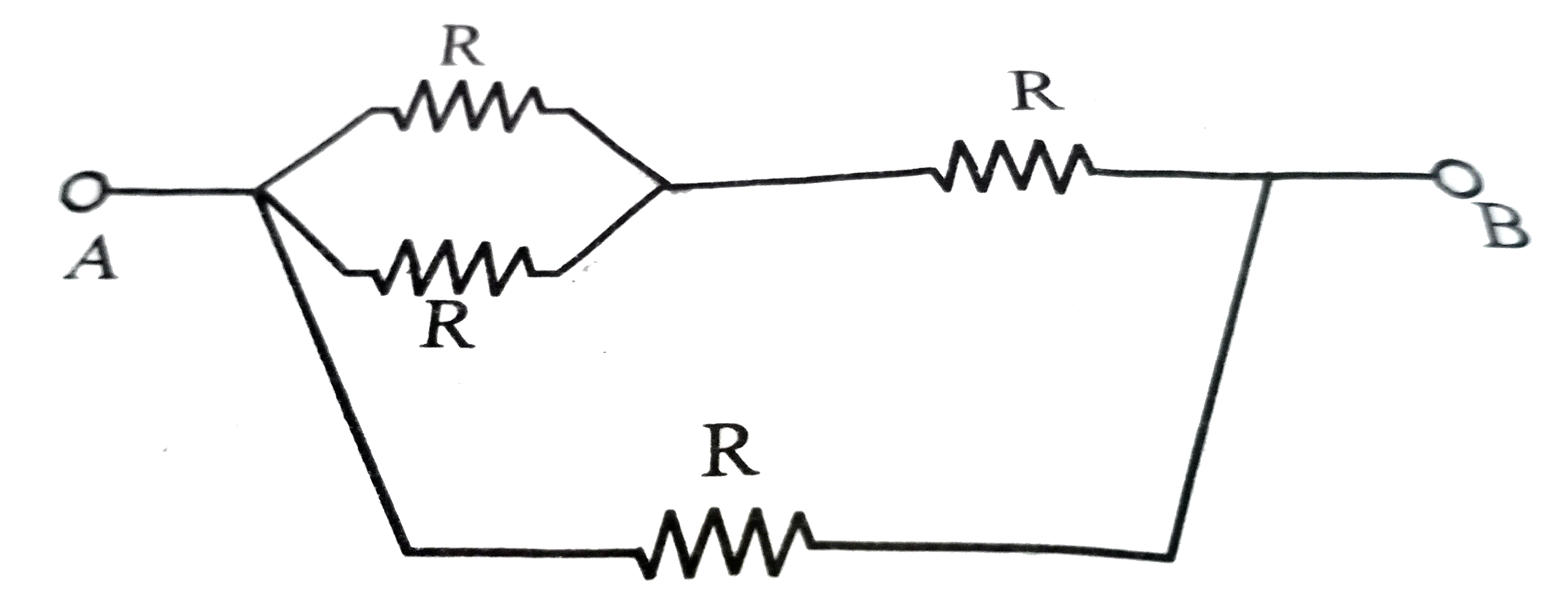
Which one of the following is the value of the resistance between points A and B in the circuit given above?
View SolutionIn the given circuit, the potential difference between the points B and D is zero
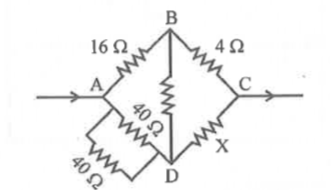
The unknown resistance (X) is
View SolutionFind the net resistance between point A and B in the circuit

View SolutionFind the equivalent capacitance of the circuit between point A and B.
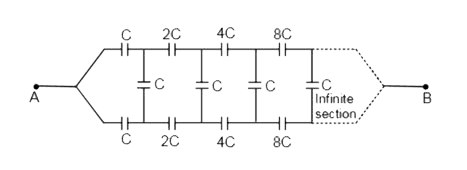
View Solution