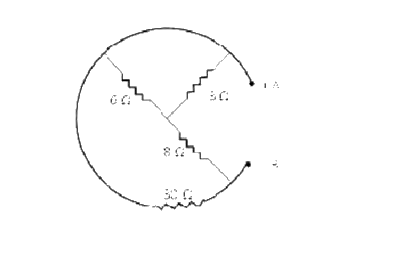
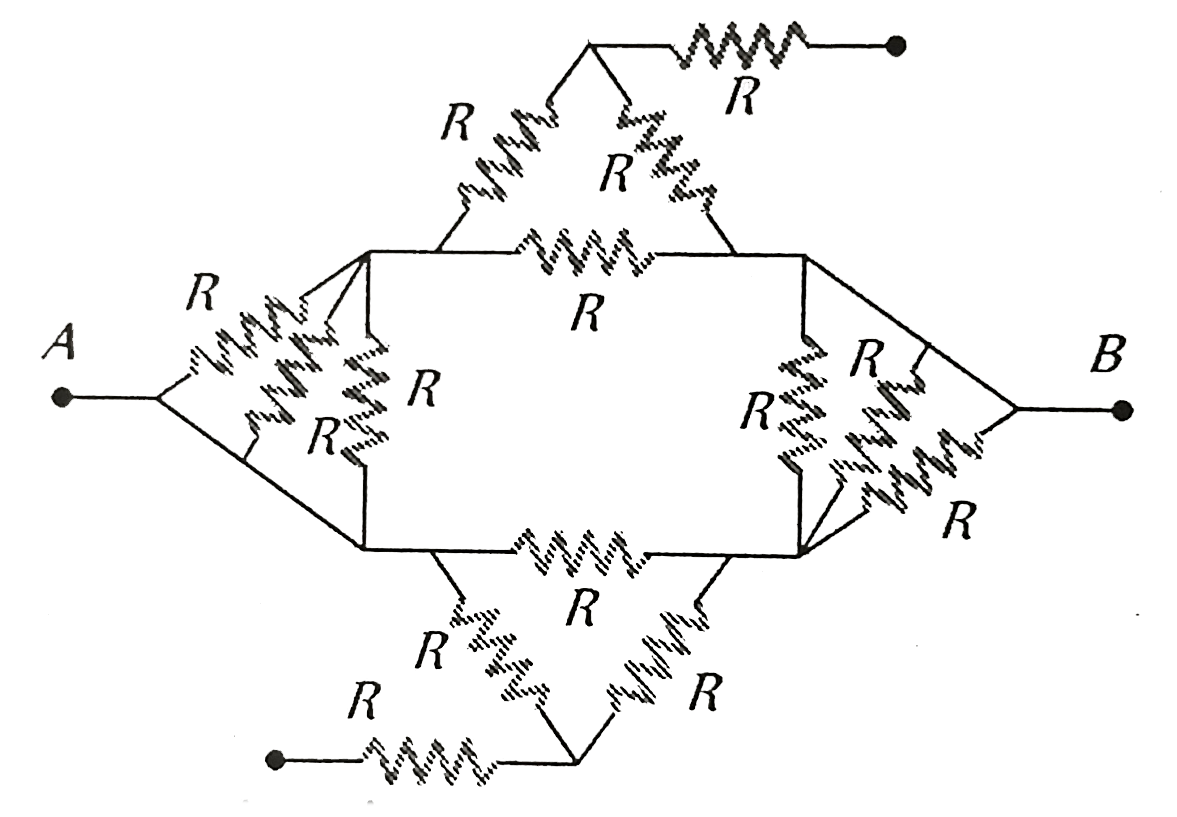
find the equivalent resistance between A and B. 
Video Solution
Text Solution
Method 1: it is a
wheatstone bridge, but it is
not balanced. There are no
series parallel connections.
But there are similar values
on input and output sides.
Here we see that even after
using symmetry, the circuit
does not reduce to series
parallel combiantion as in
previous examples. Therefore, we apply Kirchoff's voltage
law.
In loop 1 :
V−10(i−x)−5x=0
or V−10i+5x=0(i)
In loop2 : 10(i−x)−5x−5(2x−i)=0
or 10i−10x−10x+5i−5x=0
or 15i−25x=0
or x=1525i5x3i(ii)
Using (ii) and (i),
V−10i+3i=0
or VI=7ΩorReq=7Ω
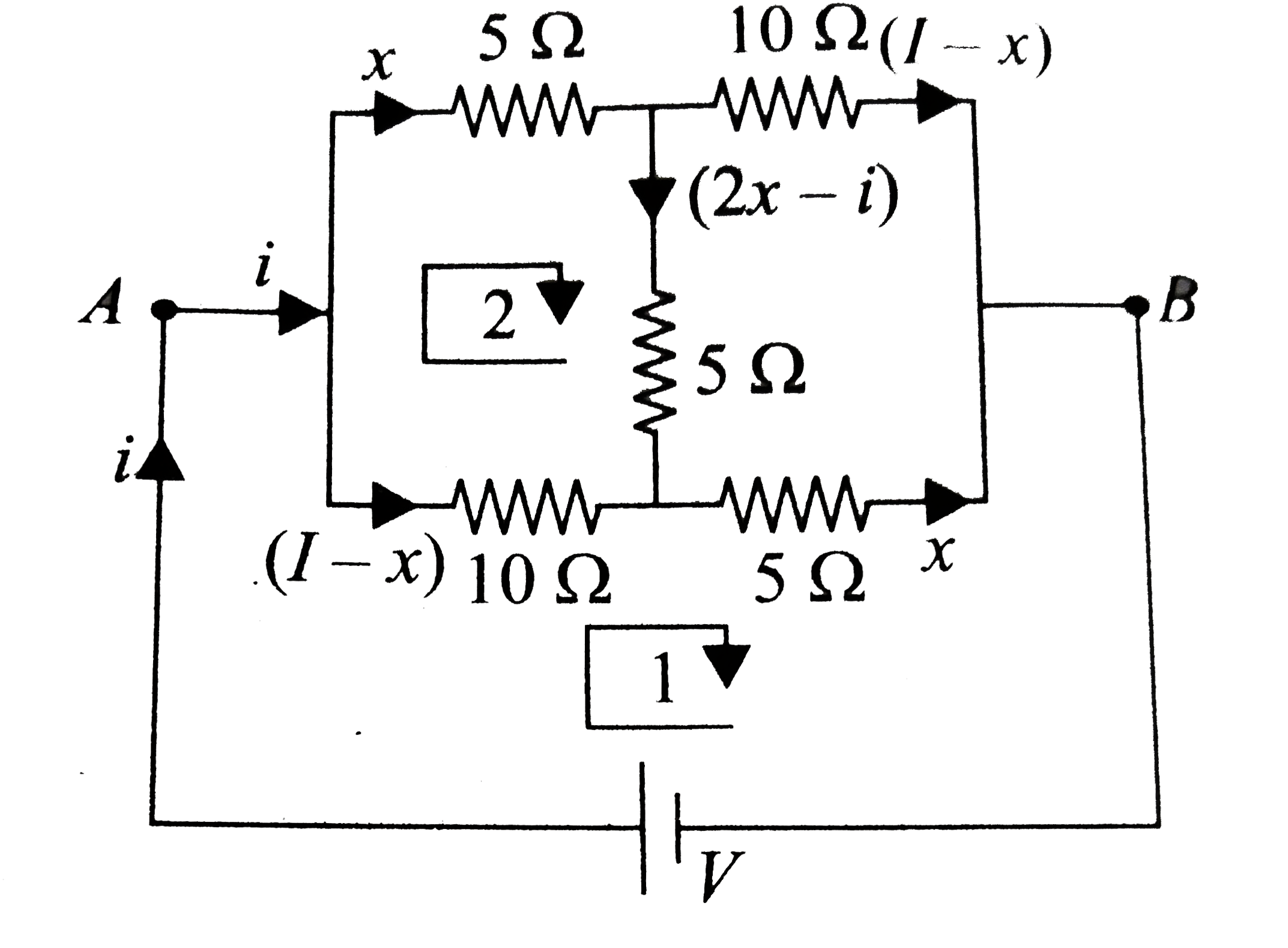
Method 2: From shifted
symmetry, it is clear that the
current in the resistances
connected across nodes 1 and
2 will be same as the resistance
connected across nodes 5 and
4. Hence, potential differences
across these resistances will
be equal.
We can state the same for the resistances connected across
the nodes 6 and 5 and nodes 2 and 3. let us assingn the potentials
of points A and B to be V and 0, respectively, then we can
assign potentials of different nodes as shown in the figure. At
node 2
(x−V)5+(x−V−x)5+(x−0)10=0
orx=47V(i)
At point A, using Kirchhoff's junction rule
I=(V−x)5+[V−(V−x)]10=2V−x10(ii)
From (i) and (ii)
VI=7Ω=Req

|
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples
12 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.1
28 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
Knowledge Check
The equivalent resistance between A and B is
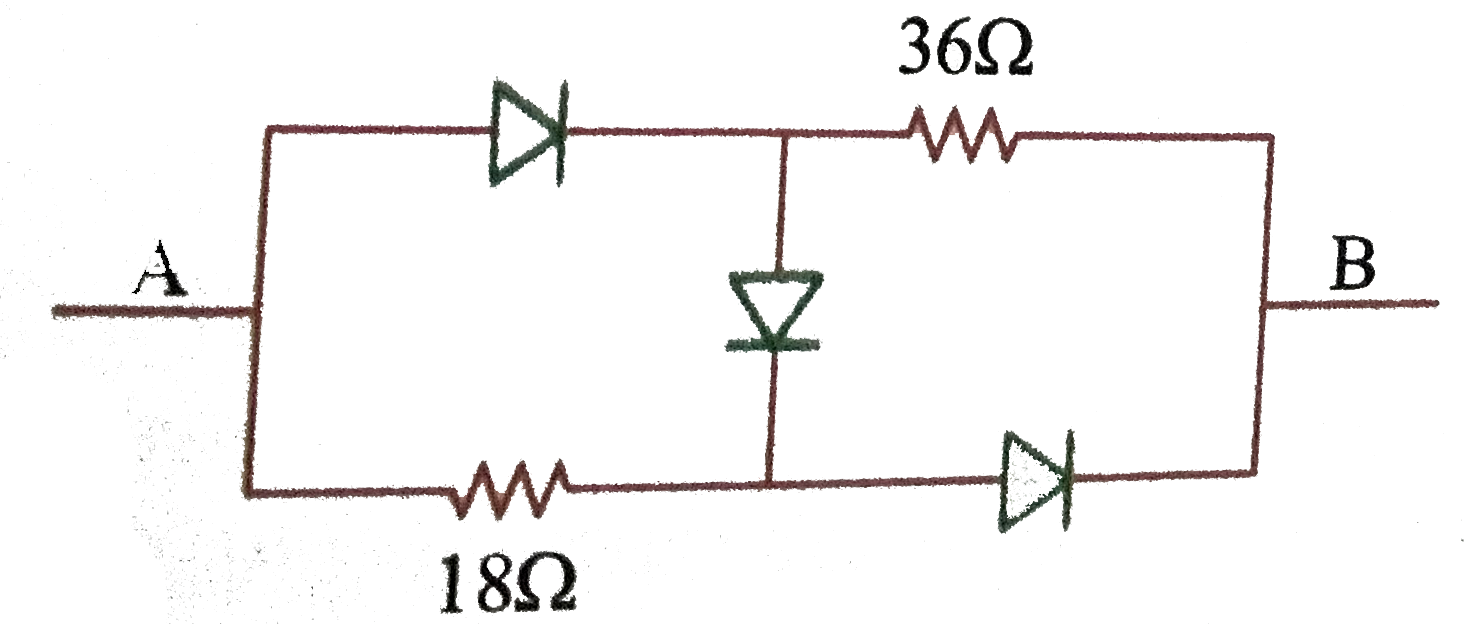 .A36Ω if VA>VBB18Ω if VA<VBCZero if VA<VB and 54Ω if VA>VBDZero if VA>VB and 54Ω If VA<VB
.A36Ω if VA>VBB18Ω if VA<VBCZero if VA<VB and 54Ω if VA>VBDZero if VA>VB and 54Ω If VA<VBEquivalent resistance between A and B is
 A34RB53RC75RDR
A34RB53RC75RDRThe equivalent resistance between A and B is:
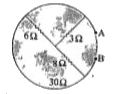 A3 ohmsB5.5 ohmsC7.5 ohmsD9.5 ohms
A3 ohmsB5.5 ohmsC7.5 ohmsD9.5 ohms
Each resistance is of 1Ω in the circuit diagram shown in figure. Find out equivalent resistance between A and B.
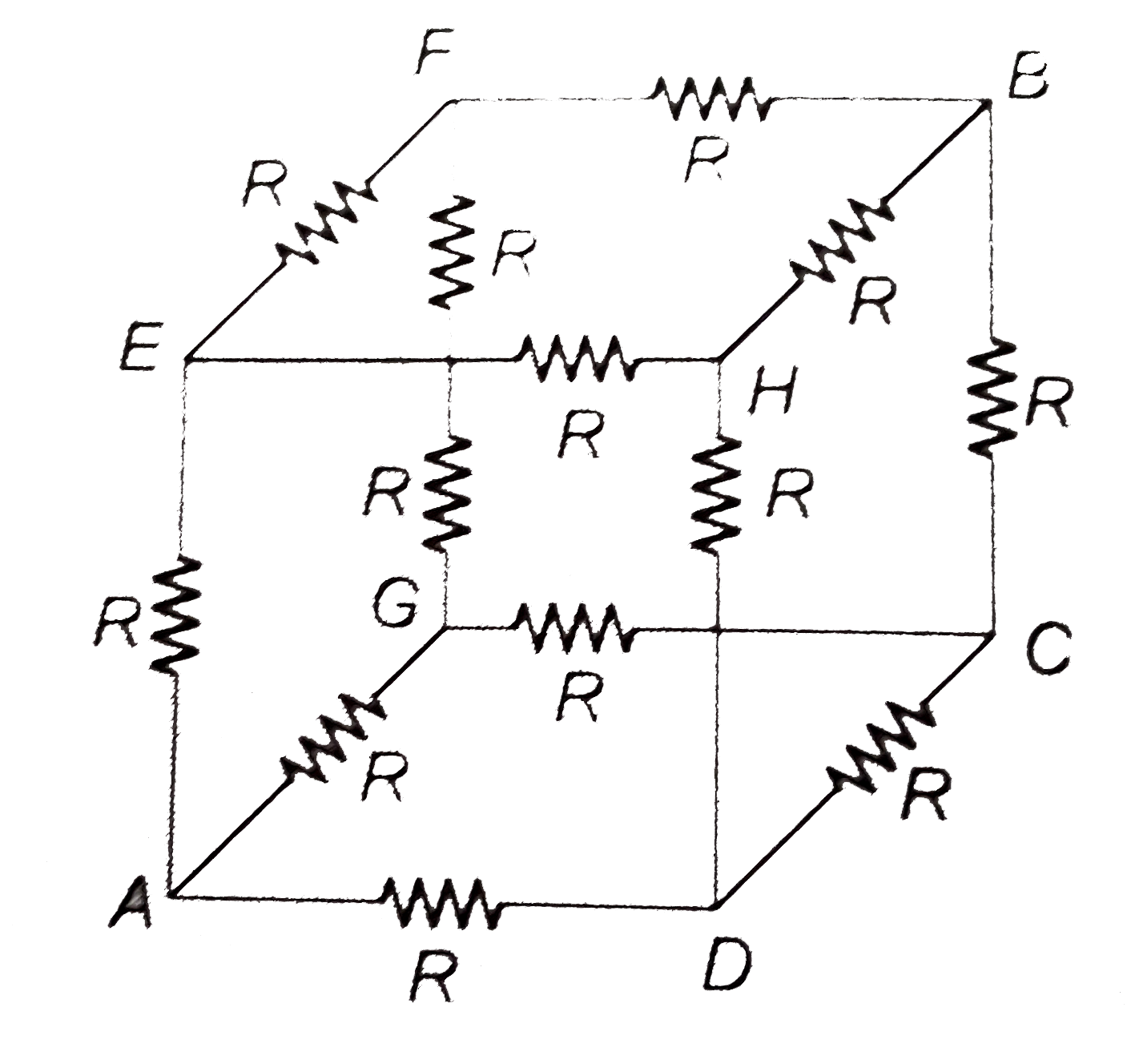
View SolutionFind the equivalent resistance between
(a) A and B and
(b) A and C.
 .
.
View SolutionFind equivalent resistance between A and B
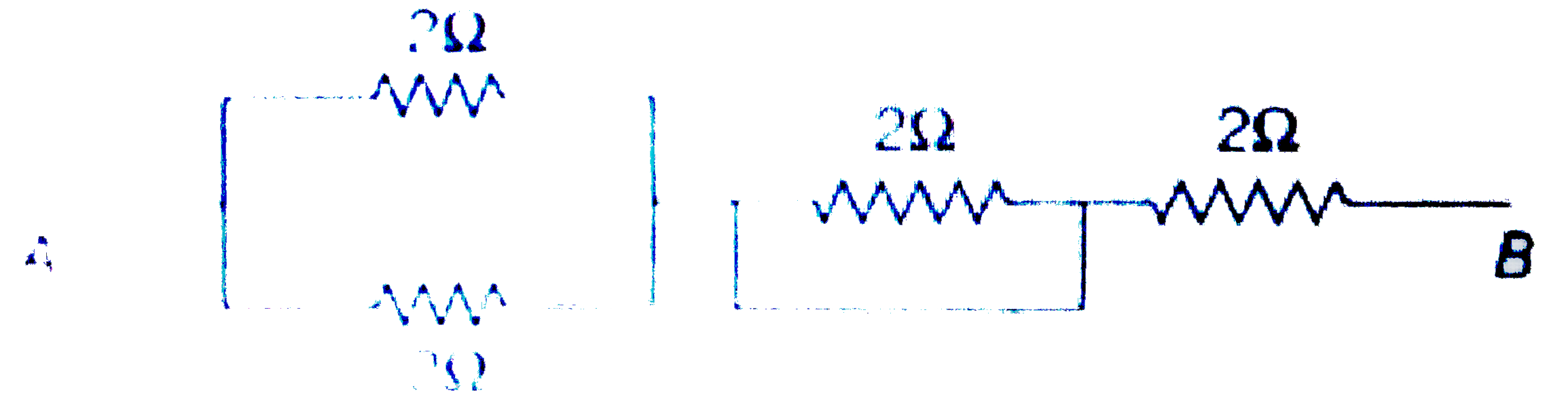
View SolutionFind equivalent resistance between A and B

View SolutionFind equivalent resistance between A and B
View Solution