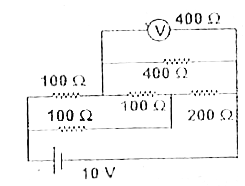
An electrical circuit is shown in figure. Calculate the potential difference across the resistor of 400Ω as will be measured by the voltmeter Vof resistance 400Ω either by applying Kirchhoff's rules or otherwise.
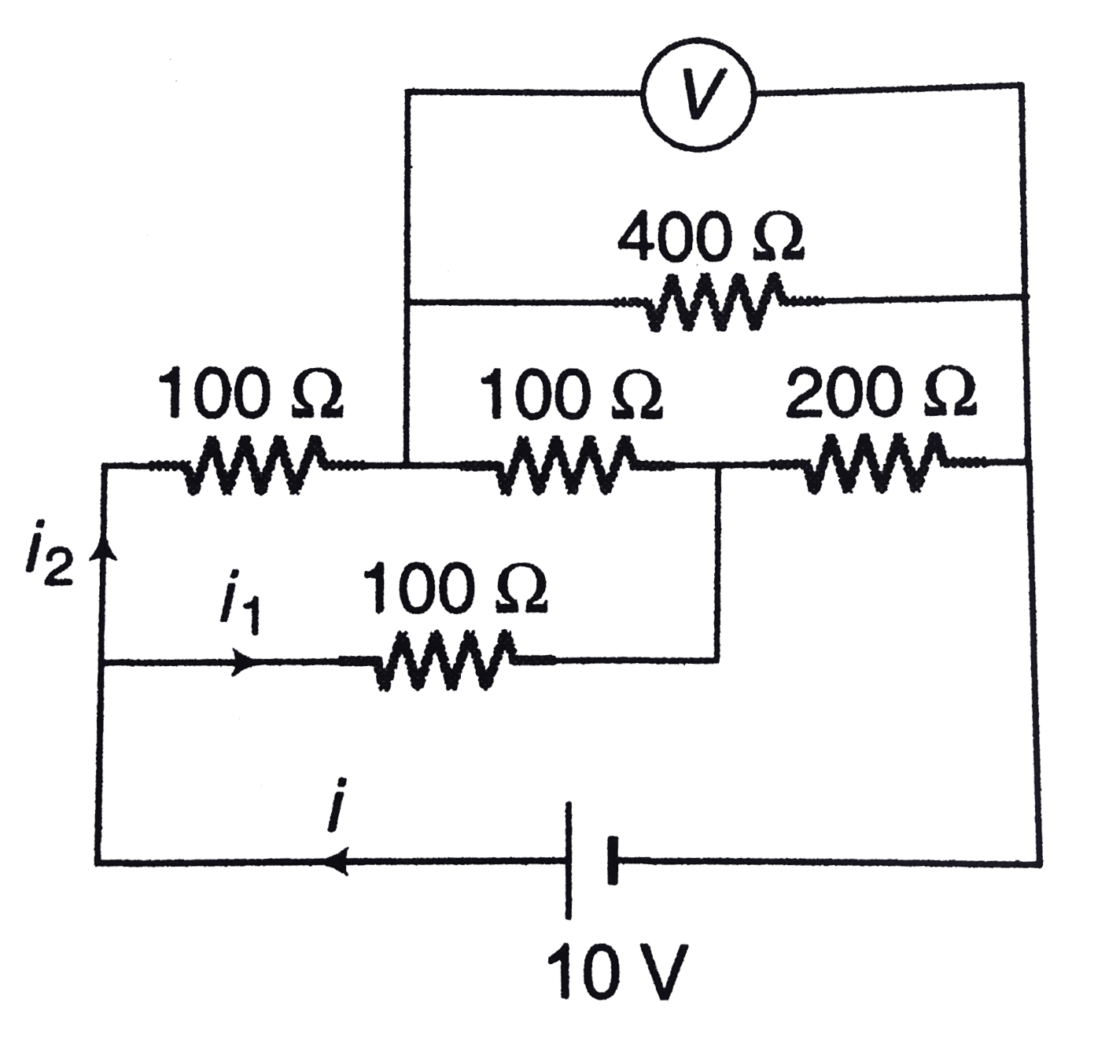
Applying kirchhoff's law in loop JMGDJ, we get
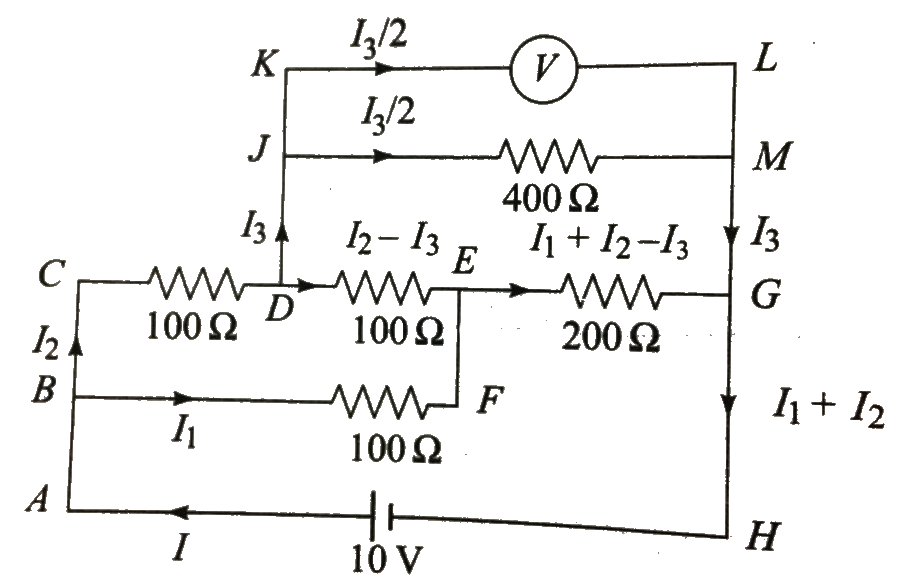
−I32×400+(I1+I2−I3)200+(I2−I3)100=0
or −500I3+200I1+300I2=0 or 2I1+3I2−5I3=0 (i)
Applying kirchhoff's law in CDEFBC, we get
−100I2−100(I2−I3)+100I1=0
or I1−2I2+I3=0 (ii)
Mulplying Eq. (i) by 2 and subracting from Eq. (i), we have
2I1+3I2−5I3−2I1+4I2−2I3=0 or I2=I3 (iii)
Applying kirchhoff's law in ABEFGHA, we get
−3I1−2I2+2I3+0.1=0 (iv)
Multiplying Eq.(ii) by 3 and adding it to Eq.(iv), we get
3I1−6I2+3I3−3I1−2I2+2I3+0.1=0
or −8I2+5I3+0.1=0 or −8I3+5I3+0.1=0
or 3I3=0.1 or I3=0.13
Therefore, potential difference across JM is
0.1/32×400=0.12×3×400
=203=6.67V
Alternative method
We can redraw the circuit as shows in Fig. 6.26. The equivalent resistance between G and D is
RGD=400×400400+400=200Ω(SinceRGERGD=REBRDB)
Therefore, it is a case of a balanced wheatstone bridge. The equivalent resistance across G and B is
RGB=300×300300+300=150Ω
Therefore, current is
I=VRGB=10150=115A
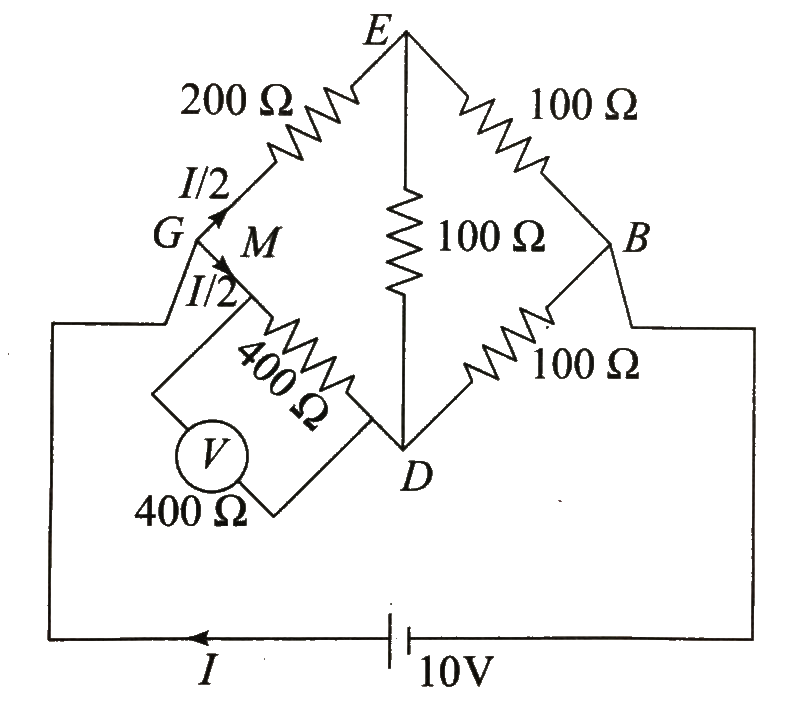
Since RGEB=RGDB, the current is divided at G into two equal
parts. The current I/2 is further divided into two equal parts at
M. Therefore, the potential difference across the voltmeter is
14×400=115×100=203V
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Exercise 6.1
15 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Subjective
18 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
Similar Questions
An elctrical circuit is shown in Fig. Calculate the potential difference across the resistor of 400 ohm, as will be measured by the voltmeter V of resistance 400 ohm, either by applying Kirchhoff's rules or otherwise.
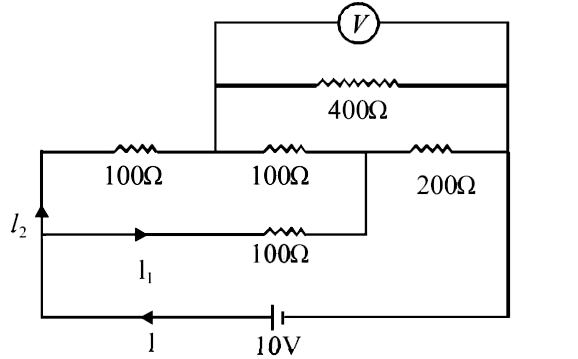 .
.
View SolutionCalculate the potential difference across the resistor of 400Ω as measured by the voltmeter Vof400Ω either by applying Kirchhoff's laws or otherwise
View Solution
Knowledge Check
In the circuit shown below:
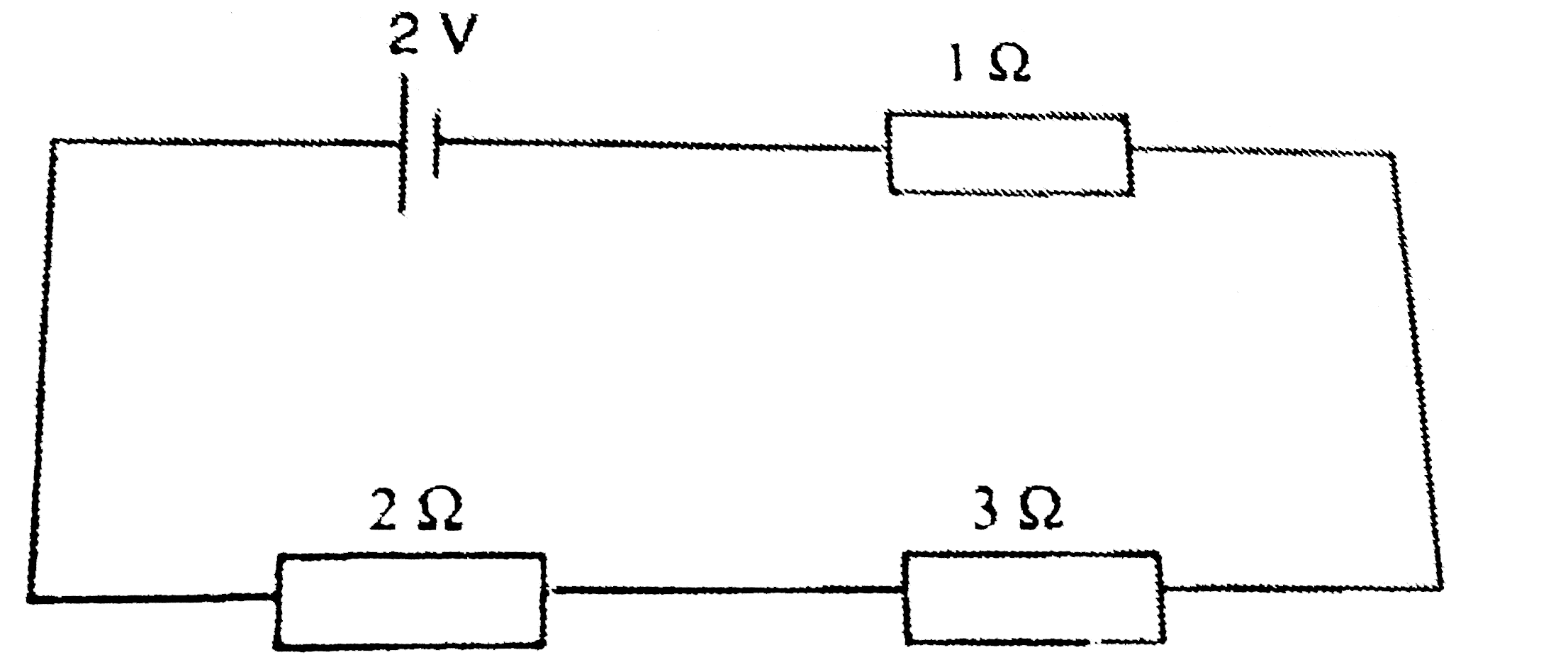
The potential difference across the 3Ω resistor is:A19VB12VC1VD2VIn the given circuit diagram, potential difference across 2Ω resistance is
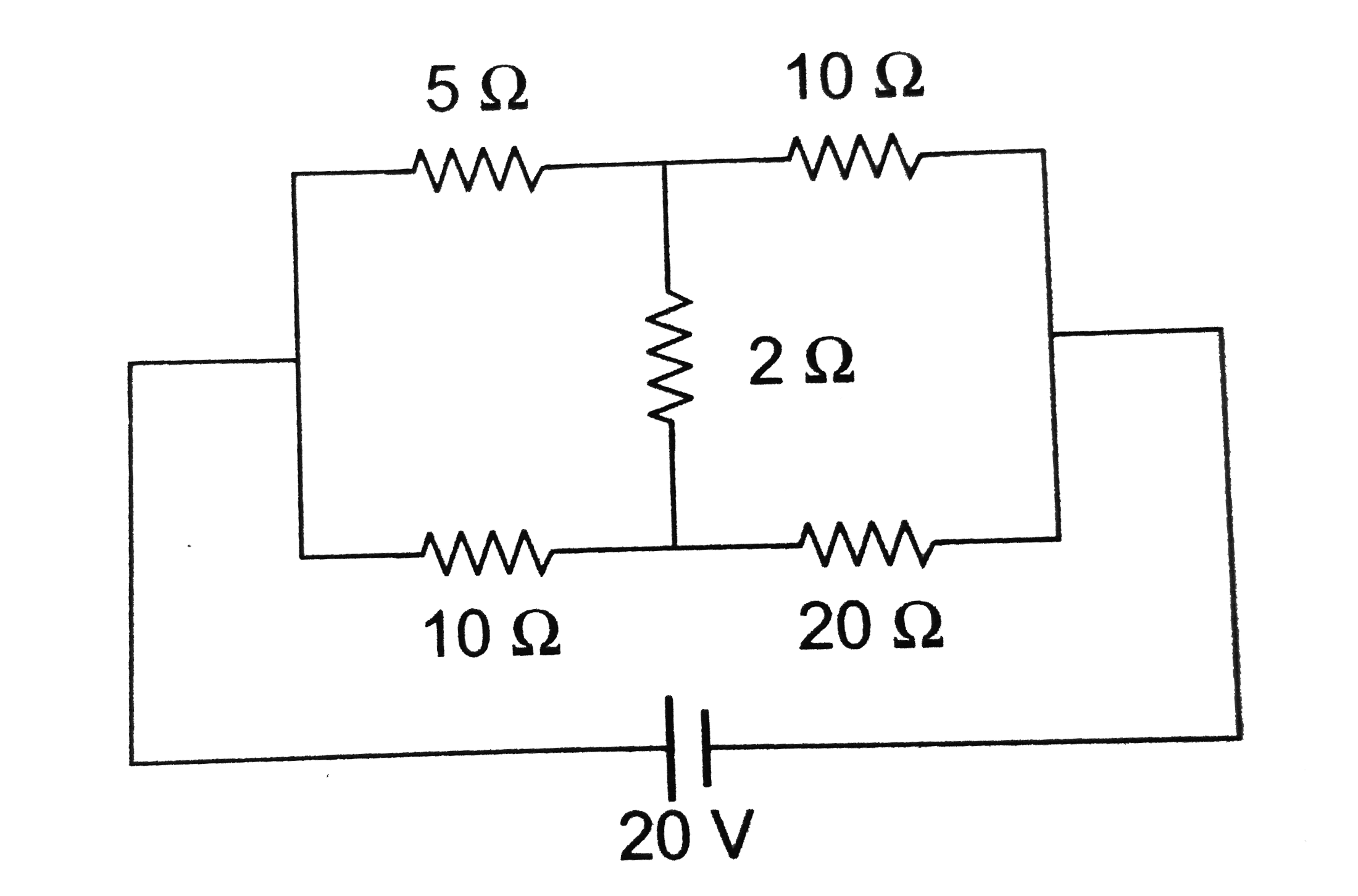 A4VB6VC20VDzero
A4VB6VC20VDzeroTo measure a potential difference across a resistor of resistance RS, a voltmeter of resistance Ry is used. To measure the potential with a minimum accuracy of 95%, then
ARv=5RBRv=15RCRv=10RDRv,≥19R
In the electrical network shown in the figure, What will be the potential difference (in volt) across 3Ω resistance ?
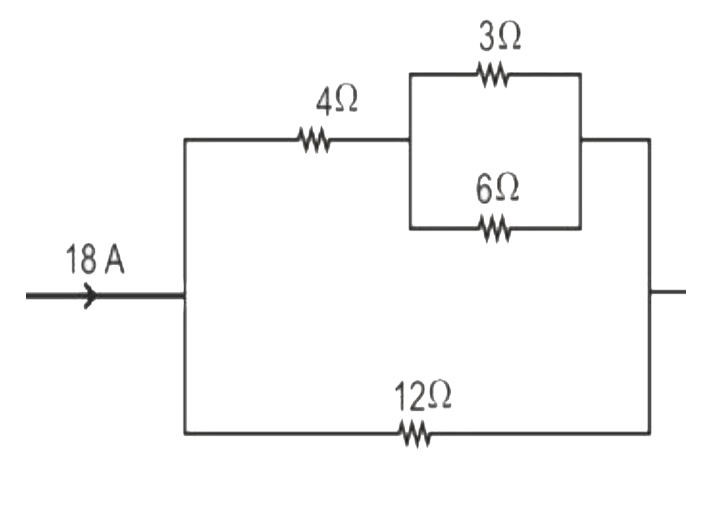
View Solution
Calculate the potential difference across the 2k Ω resistor in the circuit shown in figure. The internal resistance of the cells are negligible.
View SolutionIn the circuit diagram shown in figure, potential difference across 3Ω resistance is 20 V. Then, match the following two columns.
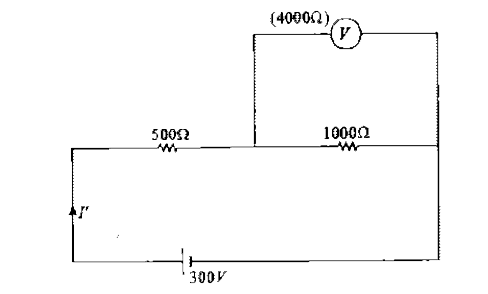
View SolutionIn the circuit shown in figure-3.387, the voltmeter is having a resistance 4000Ω. Find the percentage error in reading of this voltmeter.
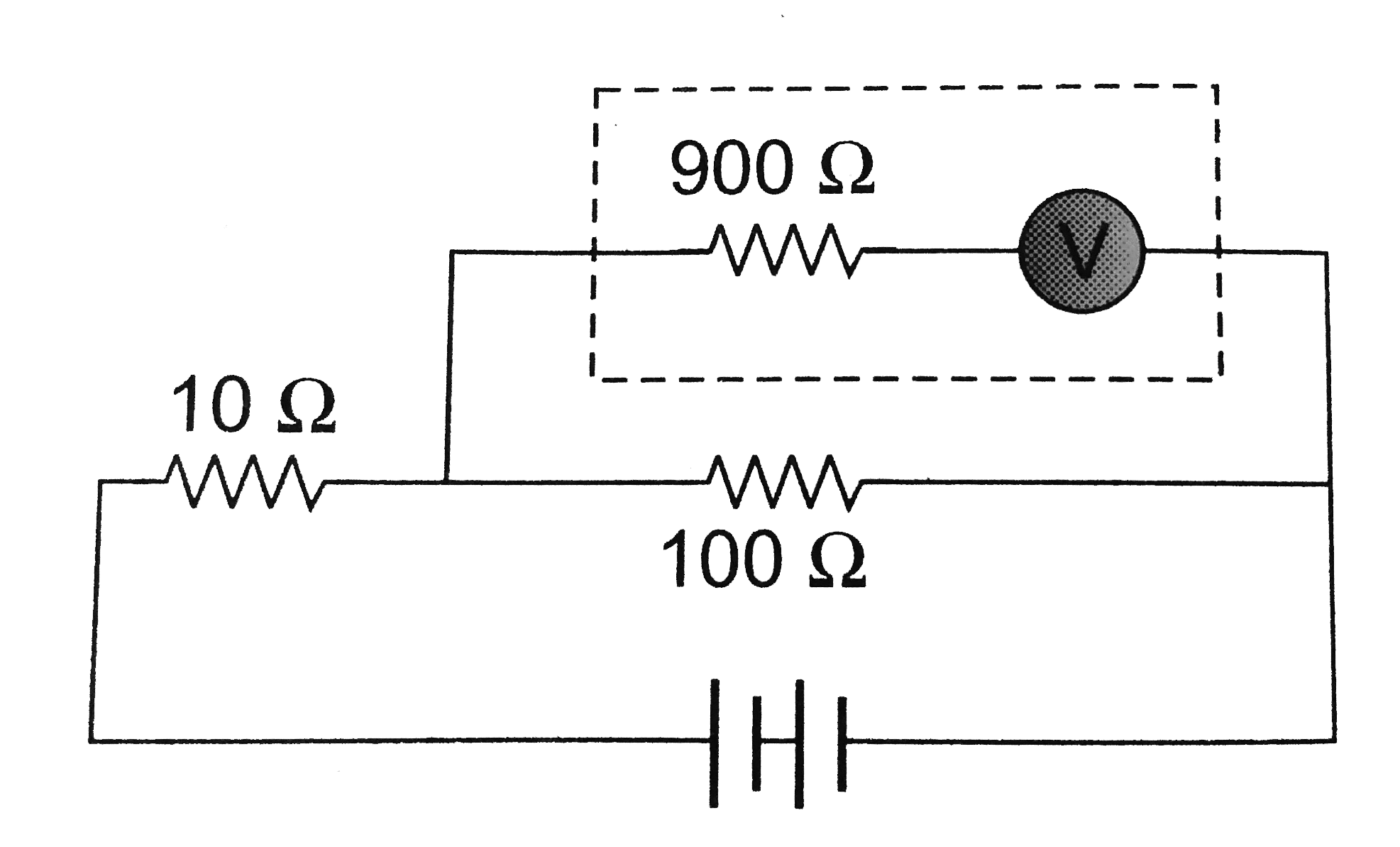
View SolutionThe potential difference across the 100Ω resistance in the following circuit is measured by a voltmeter of 900Ω resistance. The percentage error made in reading the potential difference is
View Solution
