A ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
We have
dydx=cot(θy)=√μ2y−sin2θsinθ
Here, μ=√(1+y) and θ=90∘ Therefore, dydt=y1/2
Integratin with the boundary condition that y=0 at zx=0, we get y=x2/4 to be the equation of the path of the ray through the slab, the ray will obviously exit at the point (2√2m,2m).
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
A ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y). If the thickness of the slab is d, determine the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
[y=x24]
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√1+√y. If the thickness of the slab is d, determine the equation ofthe trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View Solution
Knowledge Check
A ray of light is incident on a glass slab at an angle of 45∘. If refractive index of glass be 1.6, what is the angle of refraction ?
A45.2∘B30∘C26.2∘D15.2∘A ray of light is incident on a parallel-sided glass slab as shown in the figure. The angle of refraction for this ray of light is likely to be :
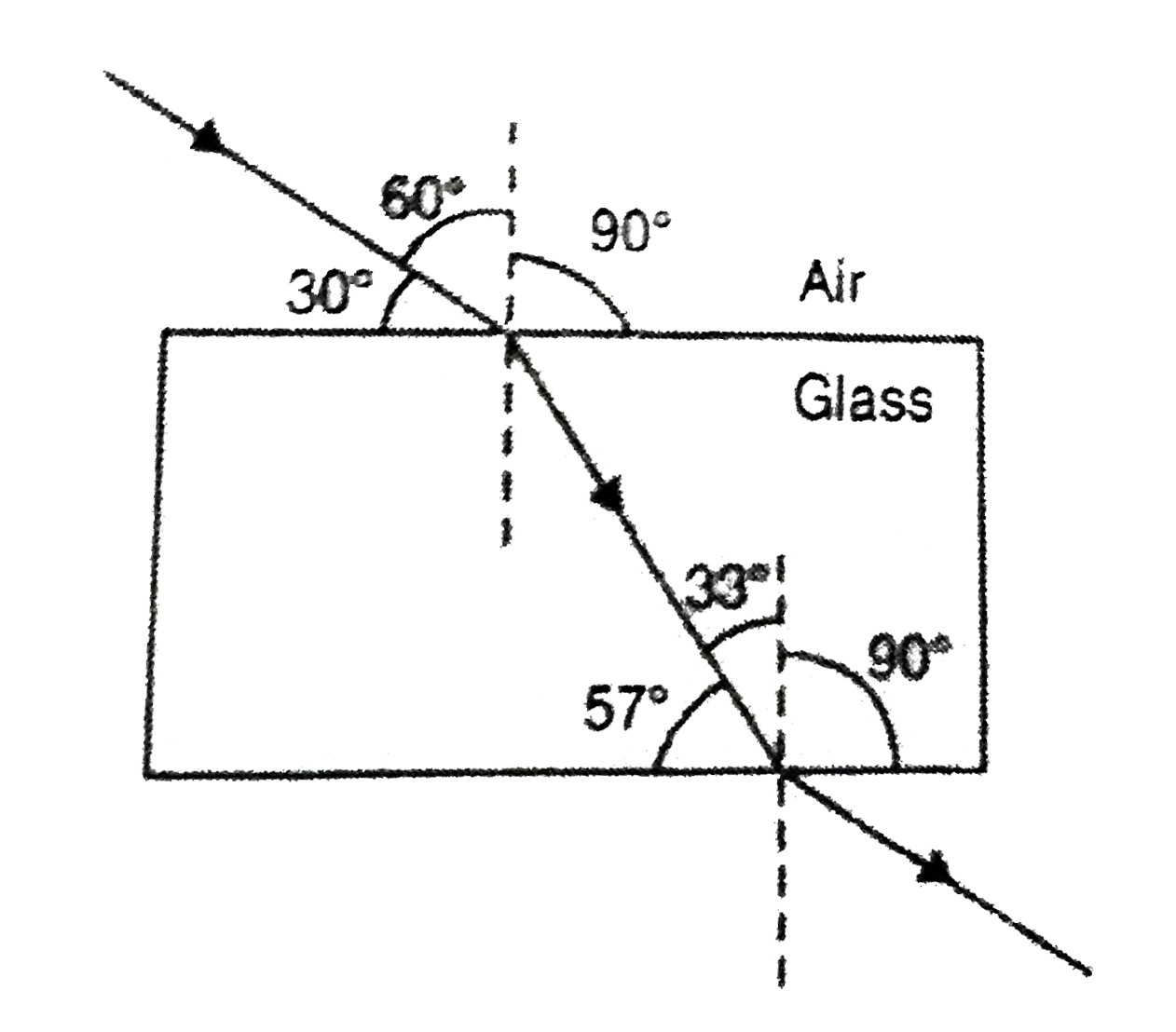 A60∘B33∘C57∘D30∘
A60∘B33∘C57∘D30∘When rays of light are incident on a glass slab, then the incident ray and emergent ray are ……….. To each other.
AperpendicularBparallelCoppositeDconcurrent
A ray of light is incident perpendicularly on a glass slab. The angle of incidence is 900.
View SolutionWhen rays of light are incident on a glass slab, then the incident ray and emergent ray are ____ to each other.
View SolutionA ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
View SolutionA ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
View SolutionWhite light is incident normally on a glass slab. Inside the glass slab,
View Solution
