A prism has refracting angle equal to $π / 2$ . It is given that $γ$ is the angle of minimum deviation and $β$ is the deviation of the ray entering at grazing incidence. Prove that $sin γ = {sin}^{2} β$ .

Text Solution

Verified by Experts

Applying condition of minimum deviation,
$μ = sin \frac{\frac{(A + γ)}{2}}{sin \frac{A}{2}} = \frac{sin \frac{A}{2} cos \frac{γ}{2} + cos \frac{A}{2} sin \frac{γ}{2}}{sin \frac{A}{2}}$
$= cos \frac{γ}{2} + cot \frac{A}{2} sin \frac{γ}{2}$
Using $A = 90^{\circ}, μ = cos \frac{γ}{2} + {cot 45}^{\circ} sin \frac{γ}{2}$
$\Rightarrow cos \frac{γ}{2} + sin \frac{γ}{2} = μ$
Squaring, ${cos}^{2} \frac{γ}{2} + {sin}^{2} \frac{γ}{2} + γ = μ^{2} \Rightarrow sin γ = μ^{2} - 1$
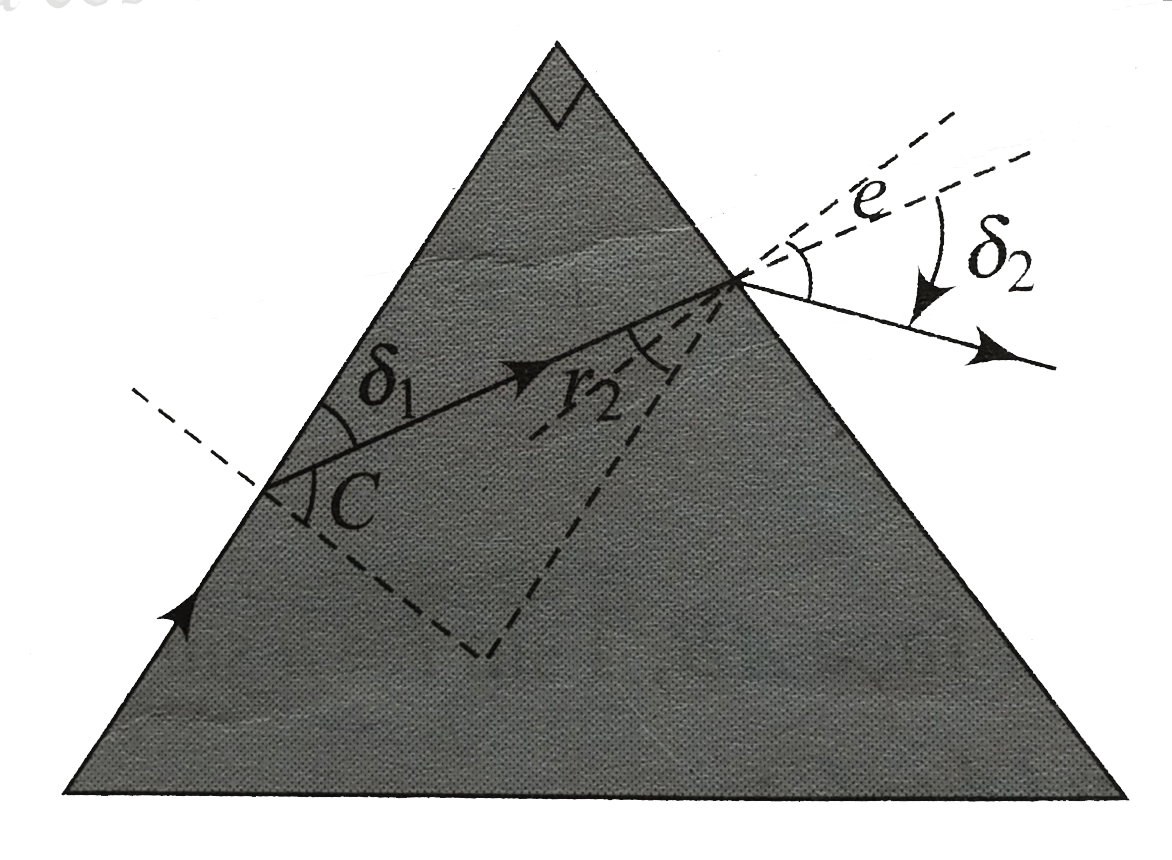
Deviation at grazing incidence,
$β = δ_{1} + δ_{2}$
$β = (\frac{π}{2} - C) + (e - r_{2})$
$\Rightarrow β (\frac{π}{2} - C) + [e - (\frac{π}{2} - C)]$
$\Rightarrow β = e$
(iii) or $sin β = sin e = μ {sin r}_{2} = μ sin (\frac{π}{2} - C)$
$\Rightarrow sin β = μ cos C$
Squaring Eq. (ii),
${sin}^{2} β = μ^{2} {cos}^{2} C \Rightarrow {sin}^{2} β = μ^{2} (1 - {sin}^{2} C)$
Using $sin C = \frac{1}{μ}, {sin}^{2} β = μ^{2} (1 - \frac{1}{μ^{2}})$
$\Rightarrow {sin}^{2} β = μ^{2} - 1$
From Eqs. (i) and (iii),
$sin γ = {sin}^{2} β$

Updated on:21/07/2023