There are two spherical surfaces of radii R1=30cm and R2=60cm. In how many ways these surfaces may be arranged to get different lenses. If all the lenses are made of glass (μ=1.5) , find the focal length of each lens.

Two surfaces may be arranged in four different ways. Using lensmaker's formuls, we can obtain the focal length of each lens as
1f=(μ−1)(1R1−1R2)
a. μ=1.5,R1=+30CM,R2=−60cm
∴1f1=(1.5−1)(130−160)=140
⇒f1=40cm (converging)
b. μ=1.5,R1=+30cm,R2=+60cm
∴1f2=(1.5−1)(130−160)=1120
⇒f2=+120cm(convering)
c. μ=1.5,R1=−30cm,R2=+60cm
∴1f3=(1.5−1)(1−30−160)=−14
⇒f3=−40cm (diverging)
d. μ=1.5,R1=−30cm,R2=−60cm
∴1f4=(1.5−1)(1−30−1−60)=−1120
⇒f4=−120cm (diverging)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
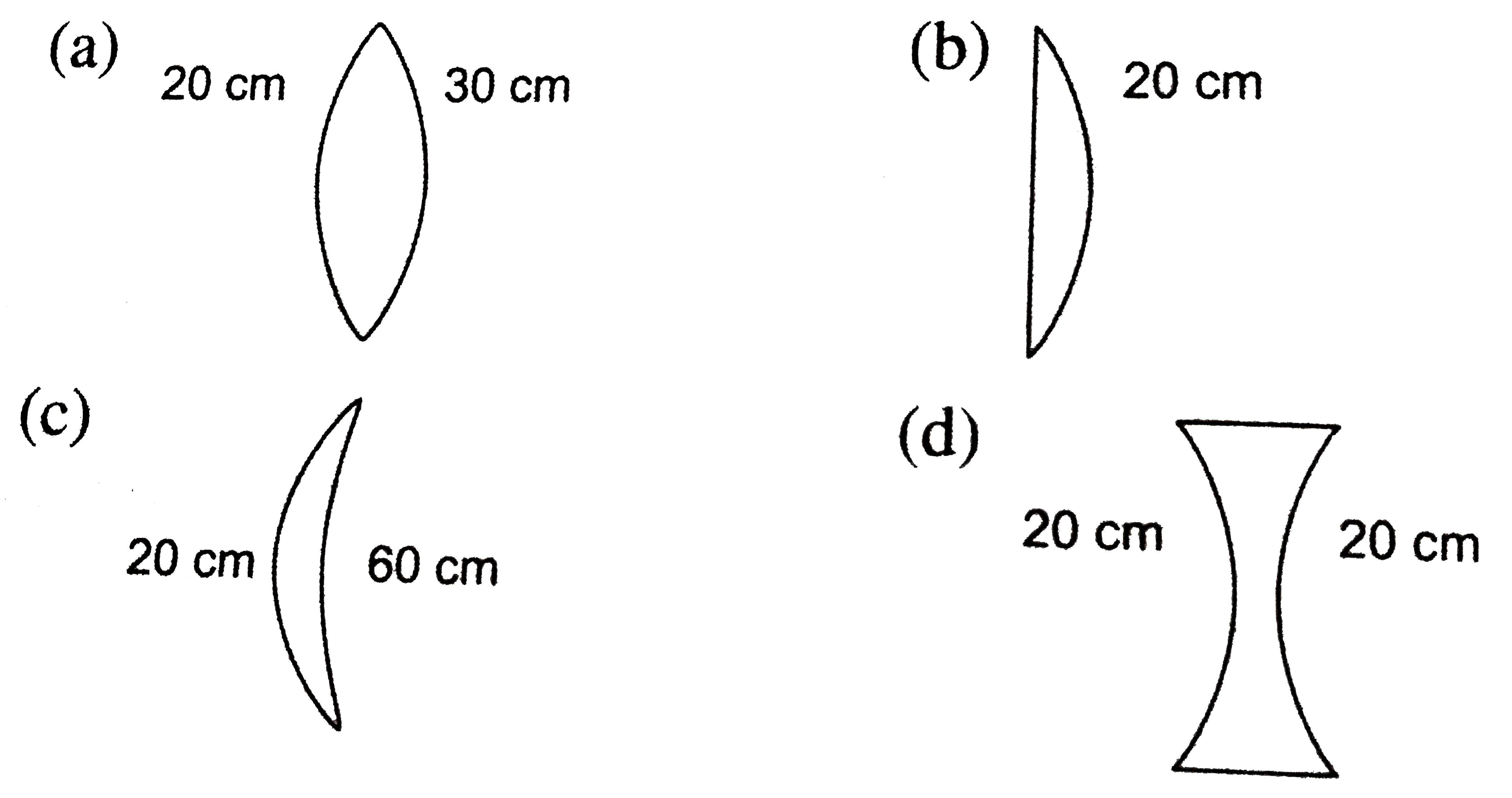
Find focal lengths of lenses made of glass (μ=3/2) and placed in air.
View SolutionA convex lens of glass (μ=1.5) is formed by combining two surfaces of radii R1=60cm and R2=30cm . It is cut into two parts in two different ways as shown in Figure .
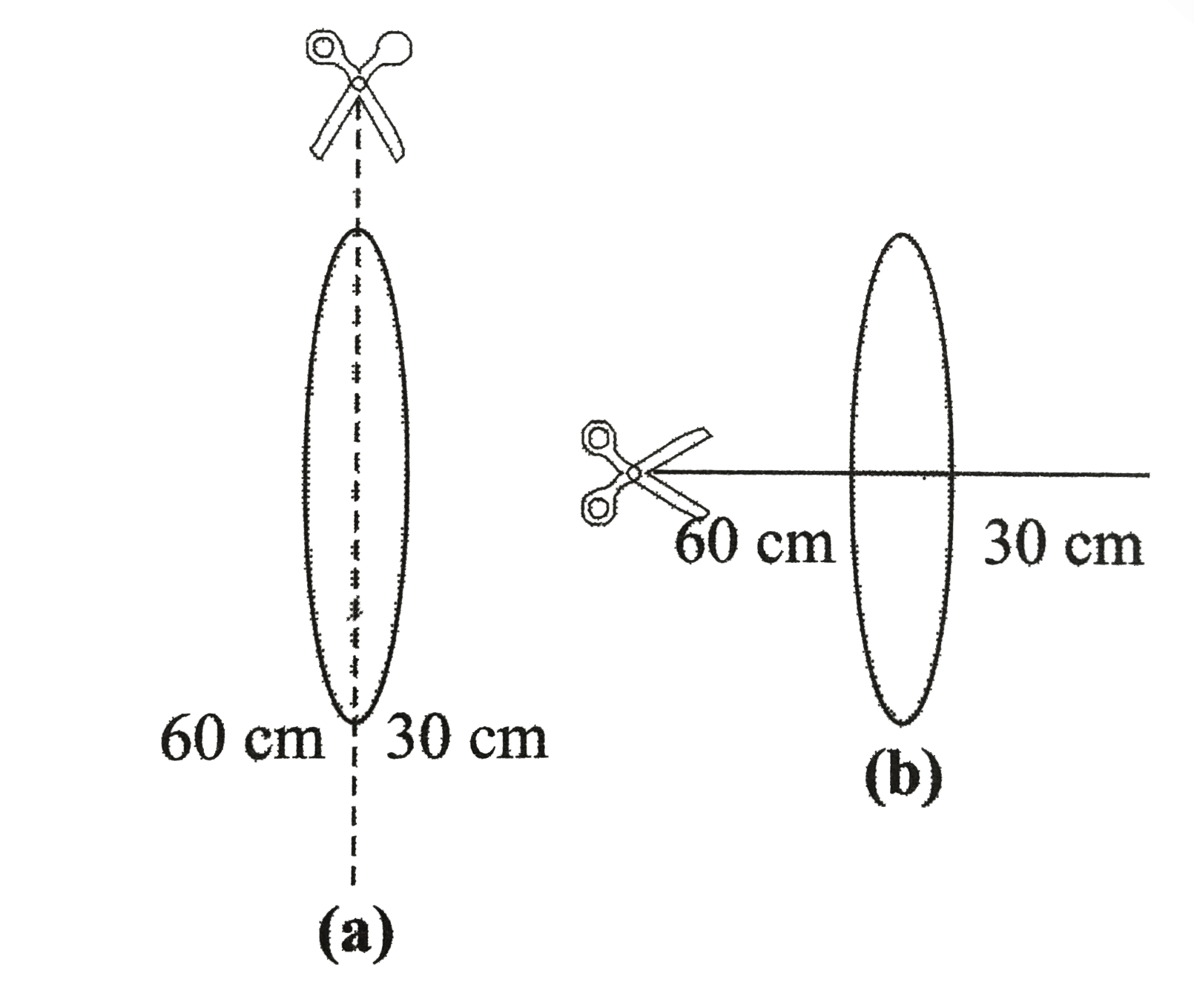
Find:
a. the focal length of the lens.
b. in figure (a), the focal length of left portion and that of the right portion.
c. in figure (b), the focal length of the upper part and that of the lower part.
View Solution
Knowledge Check
The radius of curvature of each surface of a biconcave lens made up of glass of refrative indx 1.5 is 30 cm. the focal length of the lens is
A60 cmB30 cmC−30cmD−60cmThe radii of curvature of the two surface of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5 . If the lens is concave - convex, then the focal length of the lens is :
A24 cmB10 cmC15 cmD120 cmThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
A24 cmB10 cmC15 cmD120 cm
Focal length of combination of two thin lenses is 1 m. Calculate the power of one lens if the focal length of other lens is 30 cm.
View SolutionTwo convex lenses of focal length 10 cm each are combined. What will be the focal length of the combined lens ?
View SolutionA convex lens of focal length 20cm and made of glass (μ=1.5) is immersed in water of μ=1.33 Calculate change in focal length of the lens.
View SolutionA plano-convex lens (μ=1.5) has a curved surface of radiys 15 cm. what is its focal length ?
View SolutionThe radii of curvature of the two surfaces of a lens are 20cm and 30cm and the refractive index of the material of the lens is 1.5. If the lens is concave− convex, then the focal length of lens is
View Solution
