A converging bundle of rays travel from water (refractive index 4/3 ) to glass (refractive index 1.5) through a convex interface of radius 16cm. In the absence of the interface, The rays would have converged to a point 32 cm from the pole of the interface. Where will the rays actually meet after refraction?
We now have refraction at a single curved surface. The coordinate system for this problem is shown in figure.
Refraction: Ray from water to glass
μ1=43,μ2=1.5
u=+32cm,R=+16cm
Substituting in the equation
μ2v−μ1u=μ2−μ1R
we get v=+(144/5)cm
I.e., the object appears to be 144/5 cm to the right of interface.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.615videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.721videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.412videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank39videos
GRAVITATION
Similar Questions
A converging set of ray, traveling from water to air, is incident on a plane interface. In the absence of the interface, the rays would have converged to a point O, 60 cm above the interface. However, dur to refraction the rays will bend. At what distance above the interface will the rays actually converge?
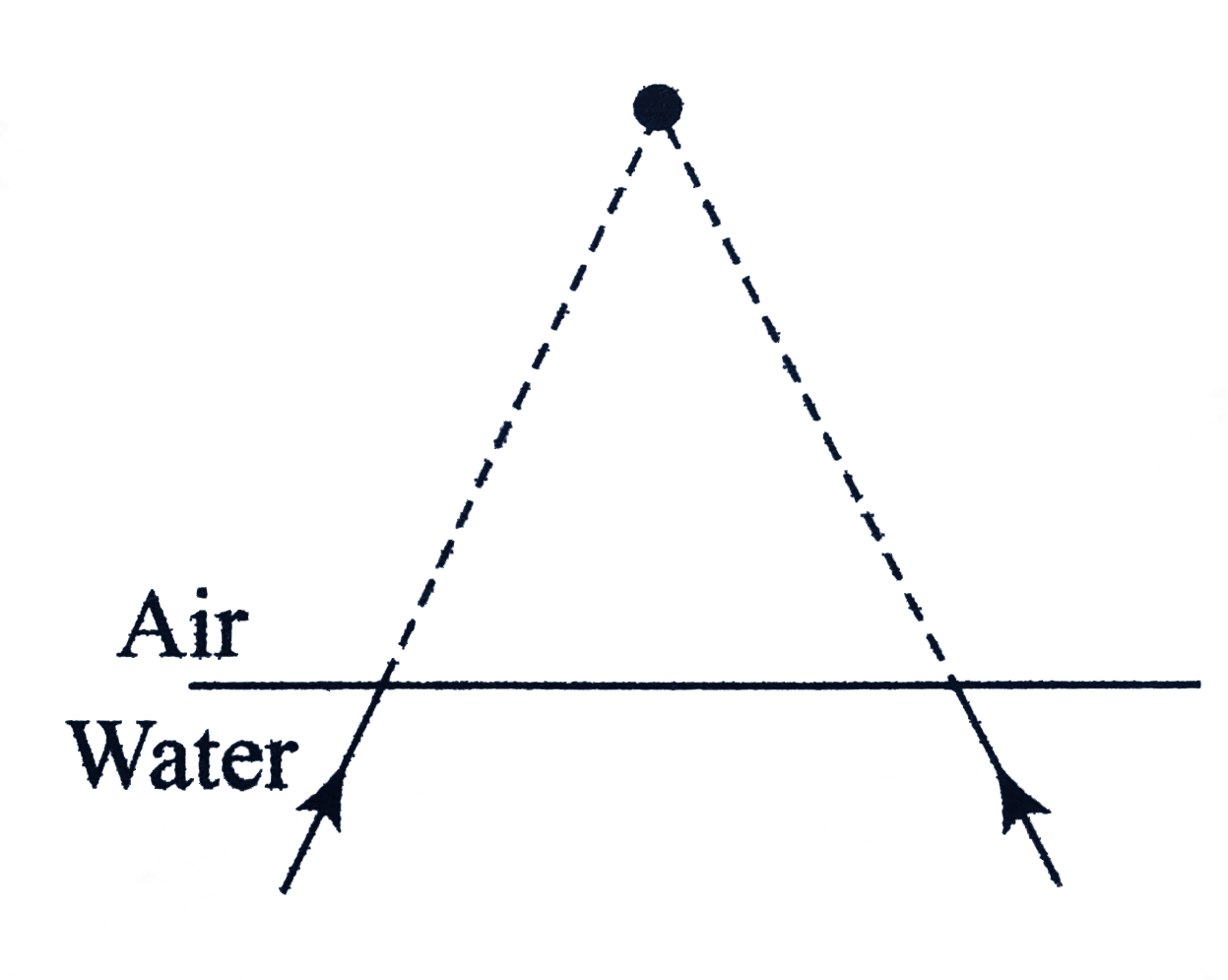 View Solution
View SolutionA converging bundle of rays is intercepted by a biconcave lens. The radii of curvature of both surfaces are 20cm and the refractive index of the material of the lens is 1.5. If the rays originially converged to a point 10cm in front of the lens, where will they now converge after passing through the lens?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
When a ray of light of frequency 6×1014 Hz travels from water of refractive index 4/3 to glass of refractive index 8/5, its
AFrequency becomes five-sixth (5/6) of its initial valueBSpeed becomes five-sixth (5/6) of its initial valueCWavelength becomes six-fifth (6/5) of its initial valueDSpeed becomes six-fifth (6/5) of its initial value - Question 2 - Select One
A ray of light travelling in glass (refractive index 1.52) enters water (refractive index 1.33) obliquely, The ray of light
ABends towards the normalBTravels along the normalCBends away from the normalDDoes not bend at all - Question 3 - Select One
A ray of light propagates from glass (refractive index =32) to water (refractive index =43). The value of the critical angel is
Asin−1(12)Bsin−1(√89)Csin−1(89)Dsin−1(34)
" I length of convex lens in air is "10cm" .Its focal length in water is (refractive index of glass "=3/2" ,refractive index of water "
View SolutionIf the refractive index from air to glass is 1.5 ,and the refractive index of water is 1.33. What is the refractive index from glass into water?
View SolutionA converging beam of light rays incident on a glasa-air interface as shown in figure. Find where these rays will meet after refraction.
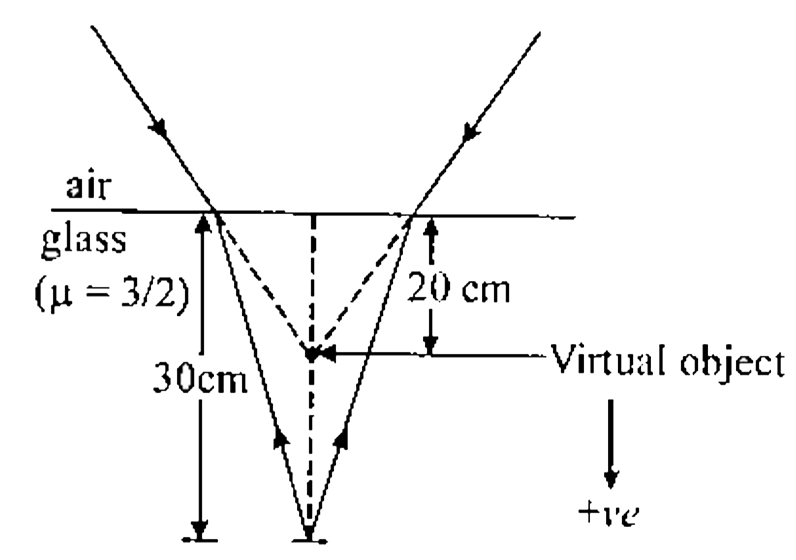 View Solution
View SolutionA ray of light is travelling from glass to air. (Refractive index of glass =1.5). The angle of incidence is 50∘. The deviation of the ray is
View SolutionLight ray is travelling from a medium of refractive index μ in to air. Angle of incidence at the interface is 53∘. Light ray is found to suffer total internal reflection. Select possible values of μ from the following :
View Solution

