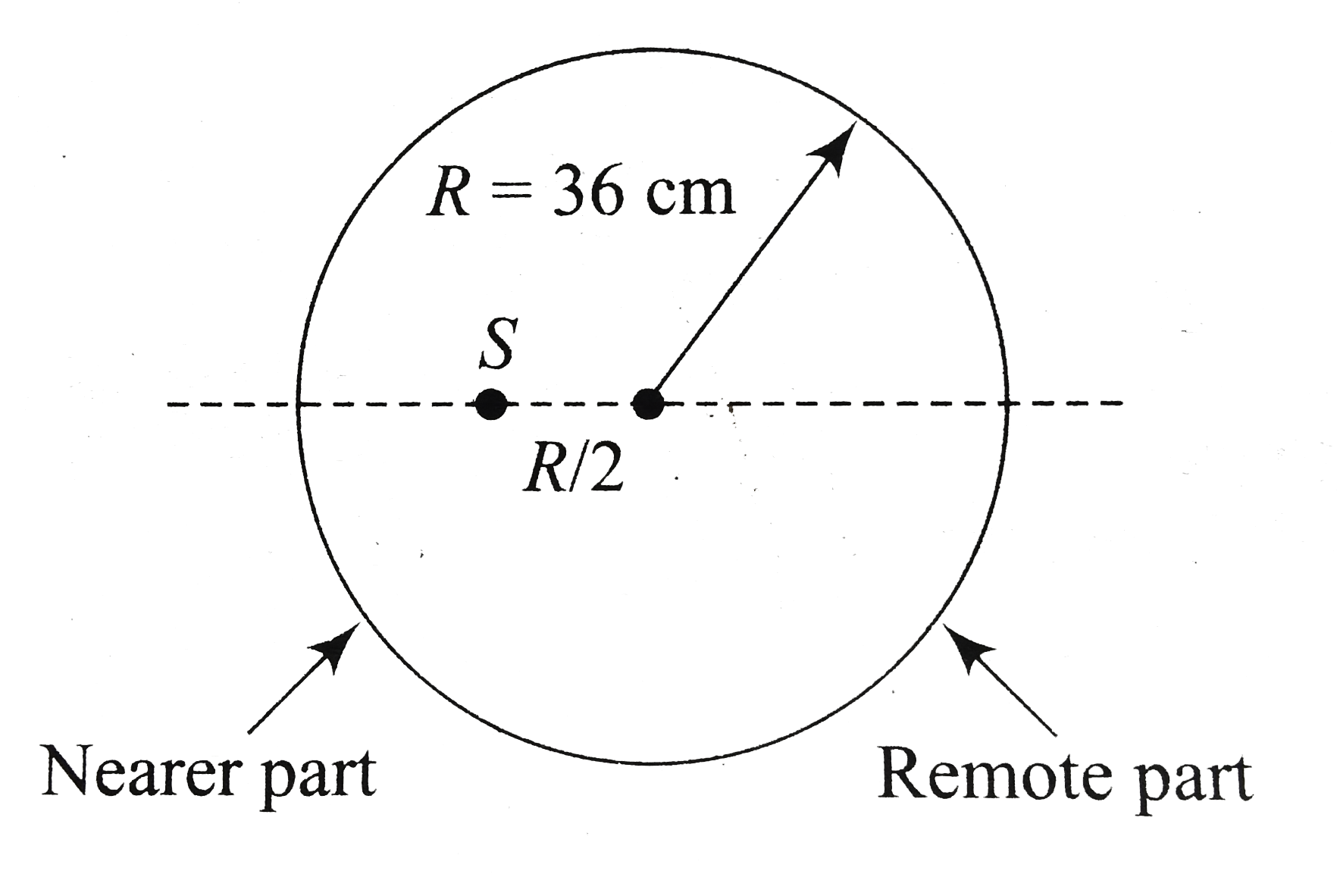
The internal surface of the walls of a sphere is specular. The radius of the sphere is R=36cm. A point source S is placed at a distance R/2 from the cneter of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflections from the remote and then nearest wall of the sphere? How will the position of the image change if the source sends light to the nearest wall first?Consider paraxial rays.
The correct Answer is:Image will be at −5R6 from near end towards source;
image will be at −R2 from remote end
Case I.
Applying mirror formula for remote part (u=−3R2,f=−R2)
v=ufu−f=−34R
Now, consider reflection from the nearer part for nearer part
u=3R4−2R=−5R4⇒v=ufu−f=∞
Reflection from remote part gives v=−2R2
Thus, the Image will be at −5R6 from near end toward source image will be at −R2 from remote end.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Single Correct
221 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.7
21 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
The internal surface of the walls of a sphere is specular (i.e. reflecting). The radius of the sphere is R=36cm. A point source S is placed at a distance R/2 from the centre of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflection from the remote and then the nearest wall of the sphere ? How wil the position of the image change if the source sends light to the nearest wall first ? Consider paraxial rays.
View SolutionThe inner surface of the wall of a sphere is perfectly reflecting. Radius of the sphere is R. A point source S is placed at a distance R/2 from the centre of the sphere. Consider the reflection of light from the farthest wall followed by reflection from the nearest wall. Where is the image of the source? Consider paraxial rays only.
View Solution
Knowledge Check
The potential at a distance R/2 from the centre of a conducting sphere of radius R will be
A0BQ8πε0RCQ4πε0RDQ2πε0RThe radius of a sphere is 21cm, what is the surface area of the sphere?
A12932cm2B4312cm2C9702cm2D5544cm2A point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
AzeroB14πε0qrC14πε0qRr2D14πε0qr2R
Radius of a sphere is 14 cm. Find the surface area of the sphere.
View SolutionThe volume of a sphere is 36πcm3. Find the surface area of the sphere.
View SolutionA hollow metal sphere of radius 5cm is charged such that the potential on its surface is 10V. The potential at a distance of 2cm from the centre of the sphere
View SolutionA hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10V. The potential at the distance 3cm from the centre of the sphere is:
View SolutionThe radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
View Solution
