In figure, ABC is the cross section of a right-angled prism and ACDE is the cross section of a gless slab. The value of θ so that light incident normally on the face AB does not cross the face AC is (given sin−1(3/5)=37∘).
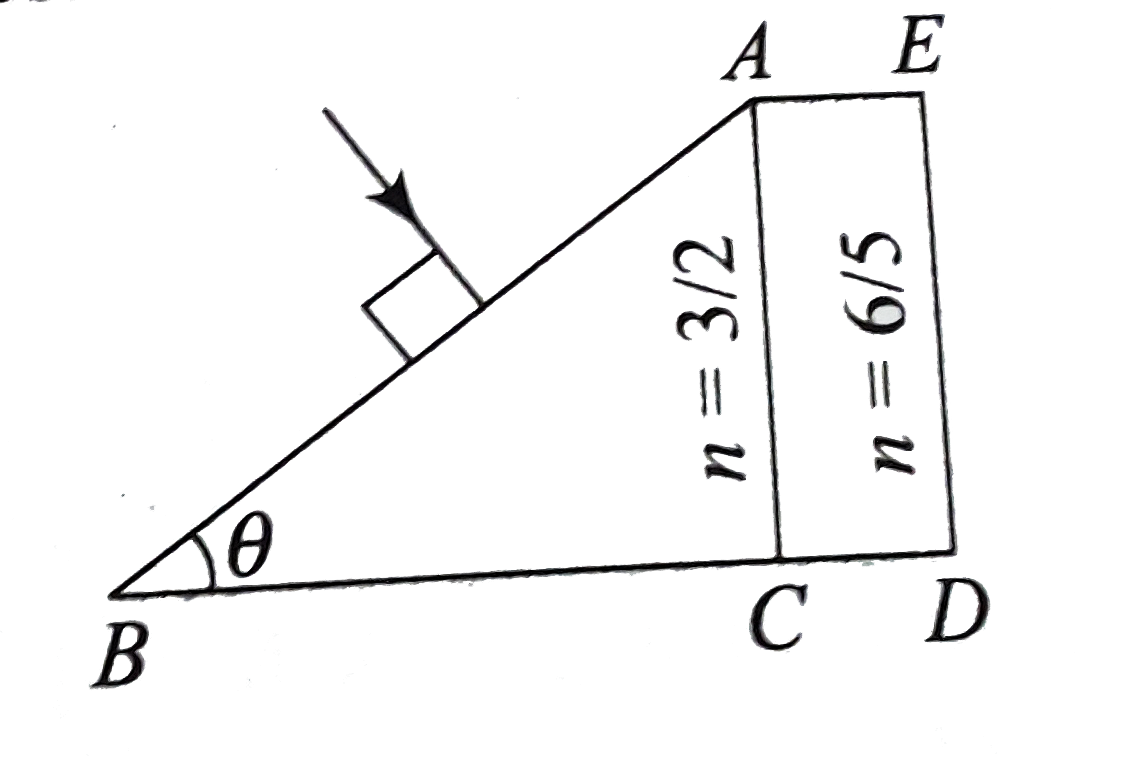
θ≤37∘
θ<37∘
θ≤53∘
θ<53∘
The correct Answer is:b.
A=90∘−θ
⇒r2=A=90∘−θ>θc
cosθ>sinθc=6/52/3=45
(θC is critical angle)
θ<cos−1(4)5=37∘

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension51videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective26videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank39videos
GRAVITATION
Similar Questions
What is the refractive index of the material of the glass prism shown in the figure, if a ray of light incident normally at the face AB emerges along the face AC?
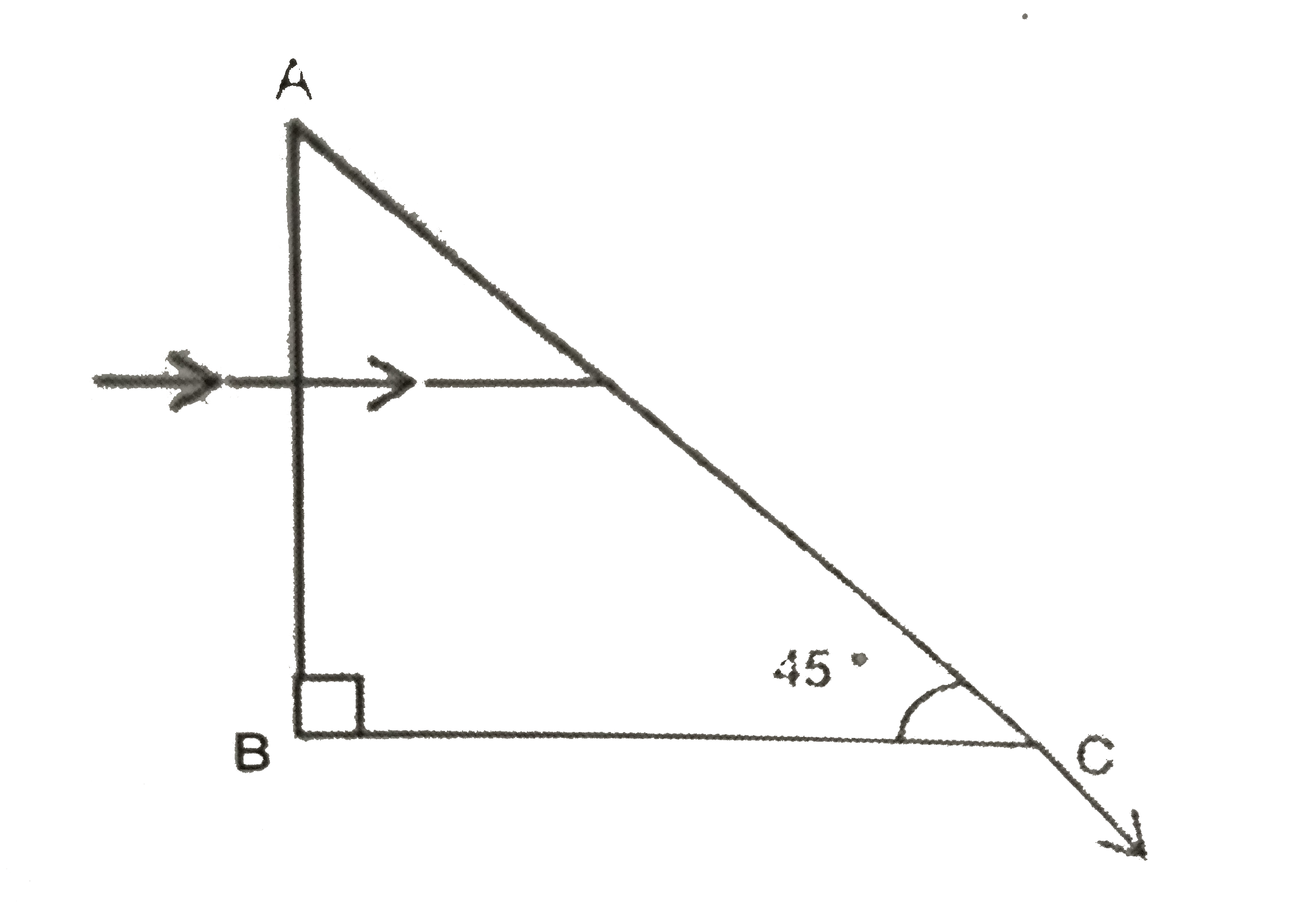 View Solution
View SolutionWhat should be the value of angle θ so that light entering normally through the surface AC of a prism (n=3/2) does not cross the second refracting surface AB?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the figure ABC is the cross-section of a right angled prism and BCDE is the cross-section of a glass slab. The value of theta so that light incident normally on the face AB does not cross the face BC is (Givensin−13/5=37∘)
 Aθ<37∘Bθ<53∘Cθ≥37∘Dθ≥53∘
Aθ<37∘Bθ<53∘Cθ≥37∘Dθ≥53∘ - Question 2 - Select One
A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if
 Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of these
Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of these - Question 3 - Select One
A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if.
 Asinθ≥89B23<sinθ<89Csinθ≤23DNone of these
Asinθ≥89B23<sinθ<89Csinθ≤23DNone of these
What should be the value of angle so that light entering normally through the surface AC of a prism (n = 3/2) does not cross the second refracting surface AB.
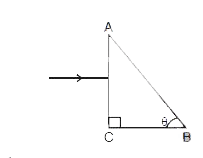 View Solution
View SolutionAt what values fo the refractive index of a recantangular prism can a ray travel as shwon in figure. The section of the prism is an isoseless triangle and the ray in normally incident onto the face AC.
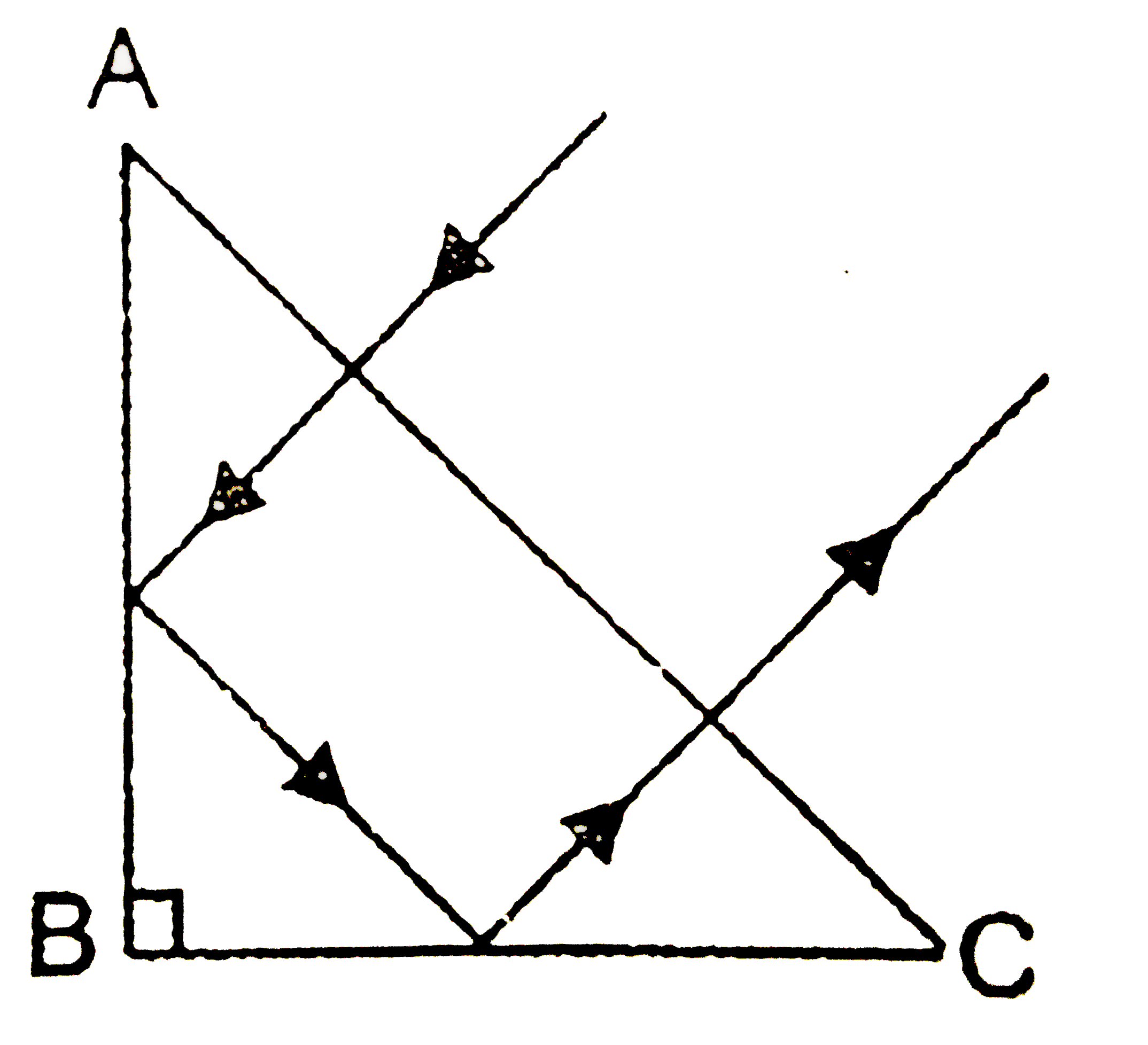 View Solution
View SolutionA light ray is incident normally on the face AB of a right-angled prism ABC(μ==1.50) as shown in figure. What is the largest angle ϕ for which the light ray is totally reflected at the surface AC ?
 View Solution
View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach the face BC, Fig. if :
 .View Solution
.View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3) . A light beam normally on the face AB is totally reflected to reach on the face BC if
 View Solution
View Solution

