Find the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:

(μ−1)Rμ
μR(μ−1)
R(μ−1)
(μ−1)R2μ
The correct Answer is:b.
μ2v−μ1u=μ2−μ1R
μ2=1,μ1=μ,u=−v,R=−R
1v−u(−u)=1−u(−R)
1v=u(μ−1)−μRuR
v=uRu(μ−1)
For v=∞,u(μ−1)−μR=0
u=μR(μ−1)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension51videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective26videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank39videos
GRAVITATION
Similar Questions
A point object is placed at a distance of 25cm from a convex lens. Its focal length is 22cm. A glass slab of refractive index 1.5 is inserted between the lens and the object, then the image is formed at infinity. Find the thickness of the glass slab (in cm).
View SolutionA glass hemispher of refractive index 4/3 and of radius 4cm is placed on a plane mirror. A point object is placed on axis of this sphere at a distance 'd' from O as shown in the figure. If the final image is formed at infinity, then find the value of d in mm .
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.

If x=2R,then the value of μisA1.5B2C3Dnone of these - Question 2 - Select One
The figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
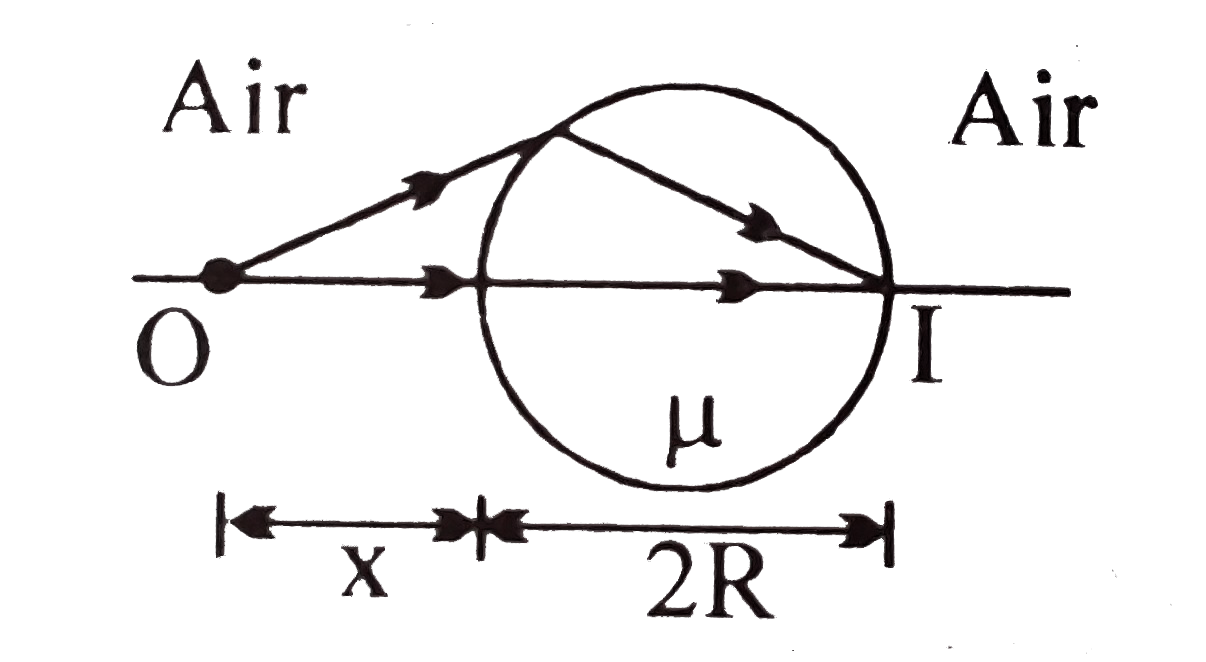 If x=∞,then the value of μ isA1.5B2C3DNone of these
If x=∞,then the value of μ isA1.5B2C3DNone of these - Question 3 - Select One
A point object is placed in front of a silvered plano convex lens of refractive index n radius of curvature R, so that its image is formed on itself. Then the object distance is equal to
 AR/2nB2R/nCR/nDnone of these
AR/2nB2R/nCR/nDnone of these
A sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
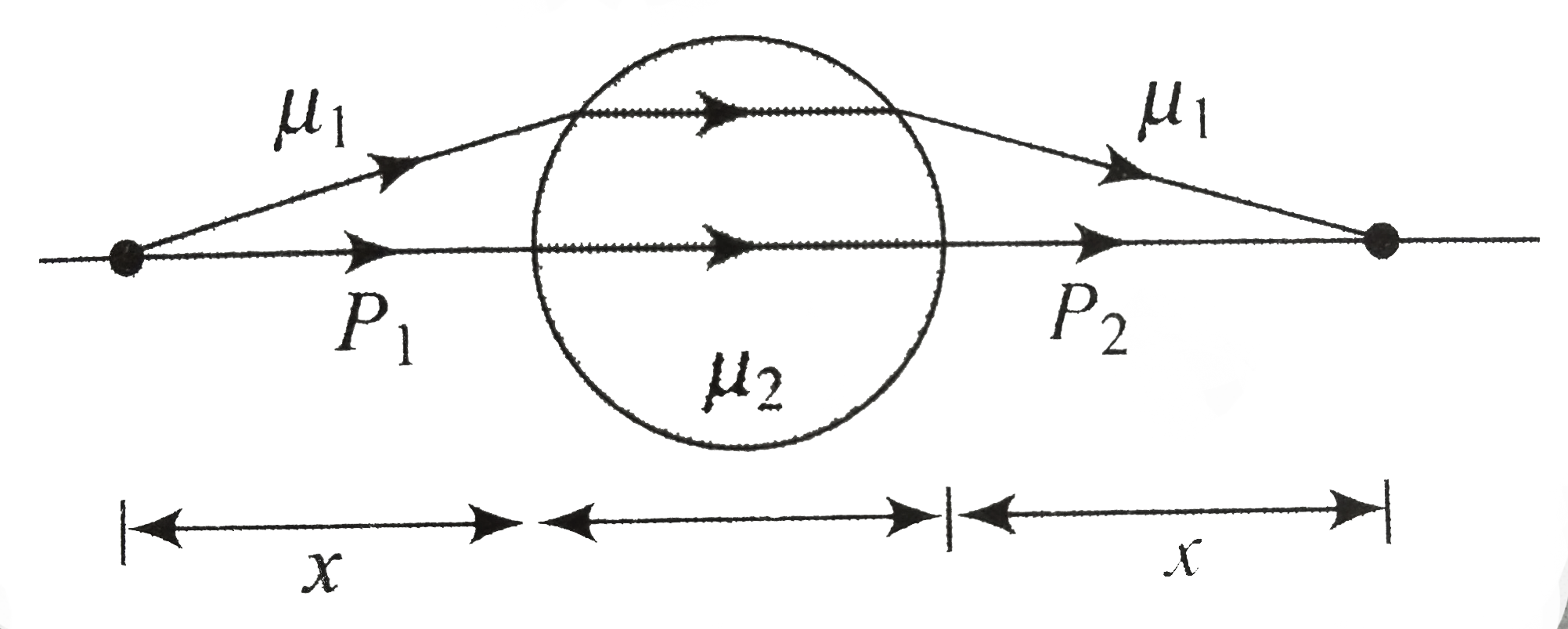 View Solution
View SolutionA point object is placed at a distance of25cmfrom a convex lens of focal length 20cm.If a glass slab of thicknesstand refractive index 1.5is inserted between the lens and object.The image is formed at infinity .Find the thickness?
View SolutionThere is a sphere of radius R and refractive index μ. At what distance from the surface of sphere should an object be placed so that real image is formed at the same distance from the sphere ?
View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
 if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byView Solution
if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byView SolutionAn object is placed at f/2 away from first focus of a convex lens where f is the focal length of the lens. Its image is formed at a distance 3f/2 in a slab of refractive index 3/2 , from the face of the slab facing the lens. Find the distance of this face of the slab from the second focus of the lens.
 View Solution
View Solution

