A parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thini convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equiconcave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.
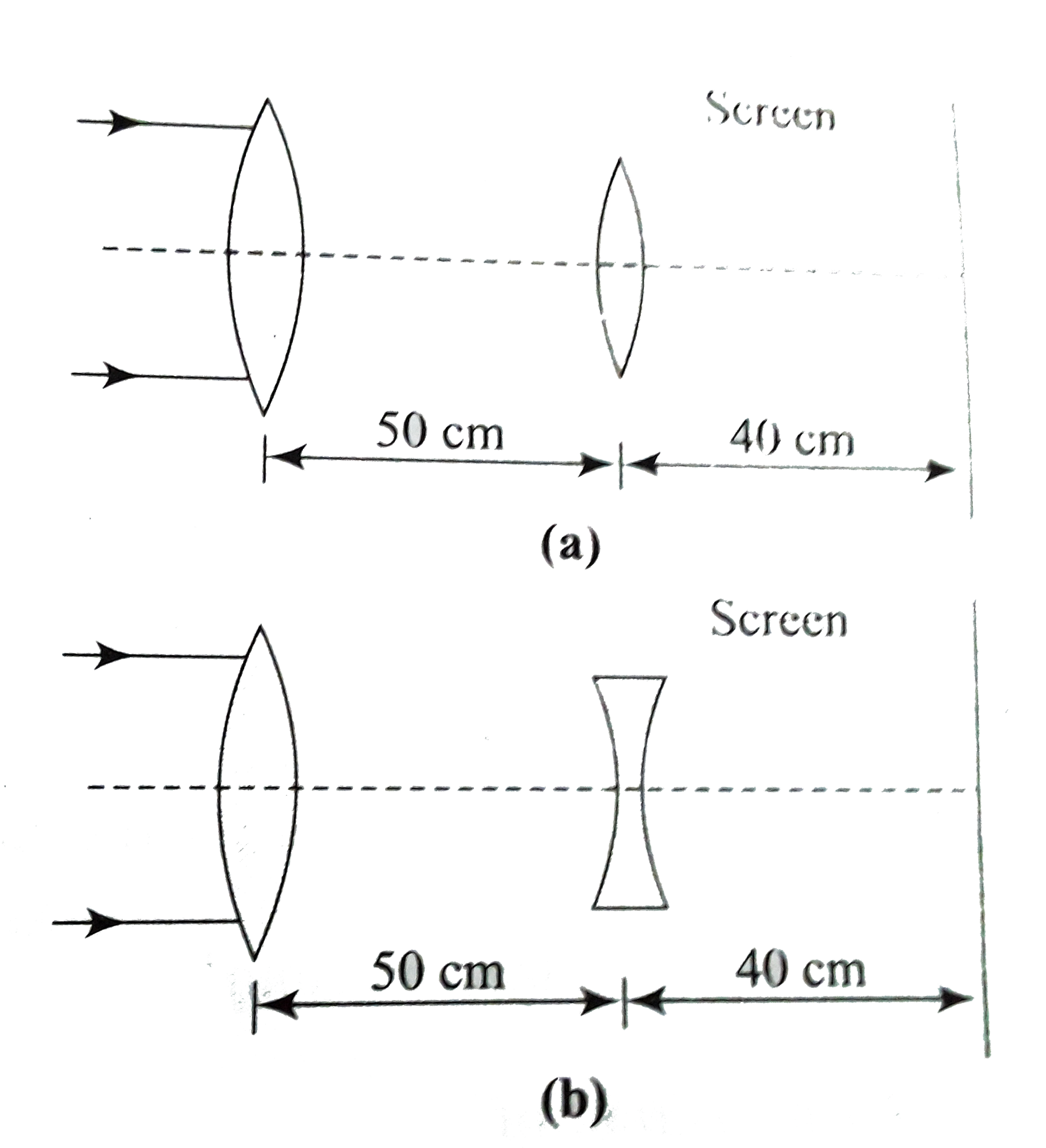
Q. Now, a liquid of refractive index μ is filled to the right of the second lens in case B such that the area illuminated in both the cases is the same. Determing the refractive index of the liquid.
1
2.5
3
1.5
The correct Answer is:c.
In case (a), the incident parallel beam emerges as a parallel beam. So area illuminated,
A1=π(1)2=πcm2
In case (b), let x be the diameter of the area illuminated.
Then,
x45=15⇒x=9cm
A2=π(92)2=814πcm2
A2A1=814
When liquid of refractive index μ is filled to the right of this lens, the first surface of the lens (radius of curvature =10cm) forms the imag at the object only. Considering the refraction at the second surface.
μ∞−1.5−10=μ−1.510 (therefore, same area ⇒υ→∞)
⇒μ=3
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives
7 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Video
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
A parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thin convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equi-concave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.
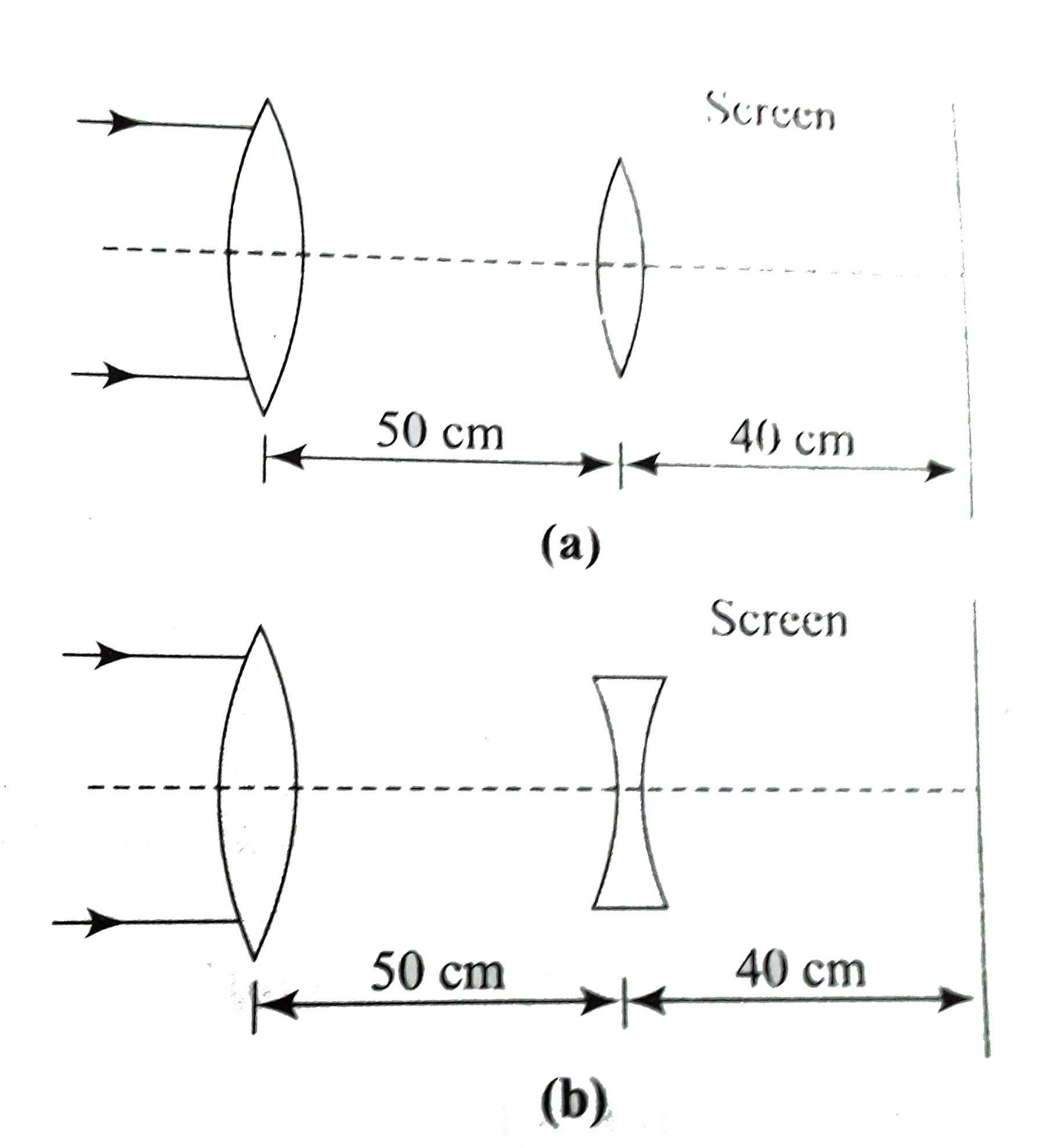
Q. Compare the area illuminated by the beam of light on the screen, which passes through the second lens in the two cases. The ratio (A2/A1) will be
View SolutionPower of a convex lens A of focal length 20 cm is more than that of a lens B of focal length 10 cm.
View Solution
Knowledge Check
A parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thini convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equiconcave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.

Q. Compare the area illuminated by the beam of light on the screen, which passes through the second lens in the two cases. The ratio (A2/A1) will beA72/5B81/4C56/3D29/2The power of a convex lens of focal length 5 cm is
A+20DB+50DC−20DD−50DA thin convex lens of focal length 10 cm and a thin concave lens of focal length 26.2 cm are in contact. The combination acts as
Aconcave lens of focal length 16.4 cmBconvex lens of focal length 16.2 cmCconcave or convex lens depends upon μof material of lensesDnone of the above.
A convex lens has focal length 20 cm. What is the power of the lens?
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionAn eye specialist prescribes spectacles having combination of convex lens of focal length 40 cm in contact with a concave lens of focal length 25 cm. The power of this lens combination in diopters is
View SolutionA convex lens of focal length 25 cm and a concave lens of focal length 10 cm are joined together. The power of the combination will be
View SolutionA convex lens of focal length 40cm is in contact with a concave lens of focal length 25cm. The power of the combination is
View Solution
