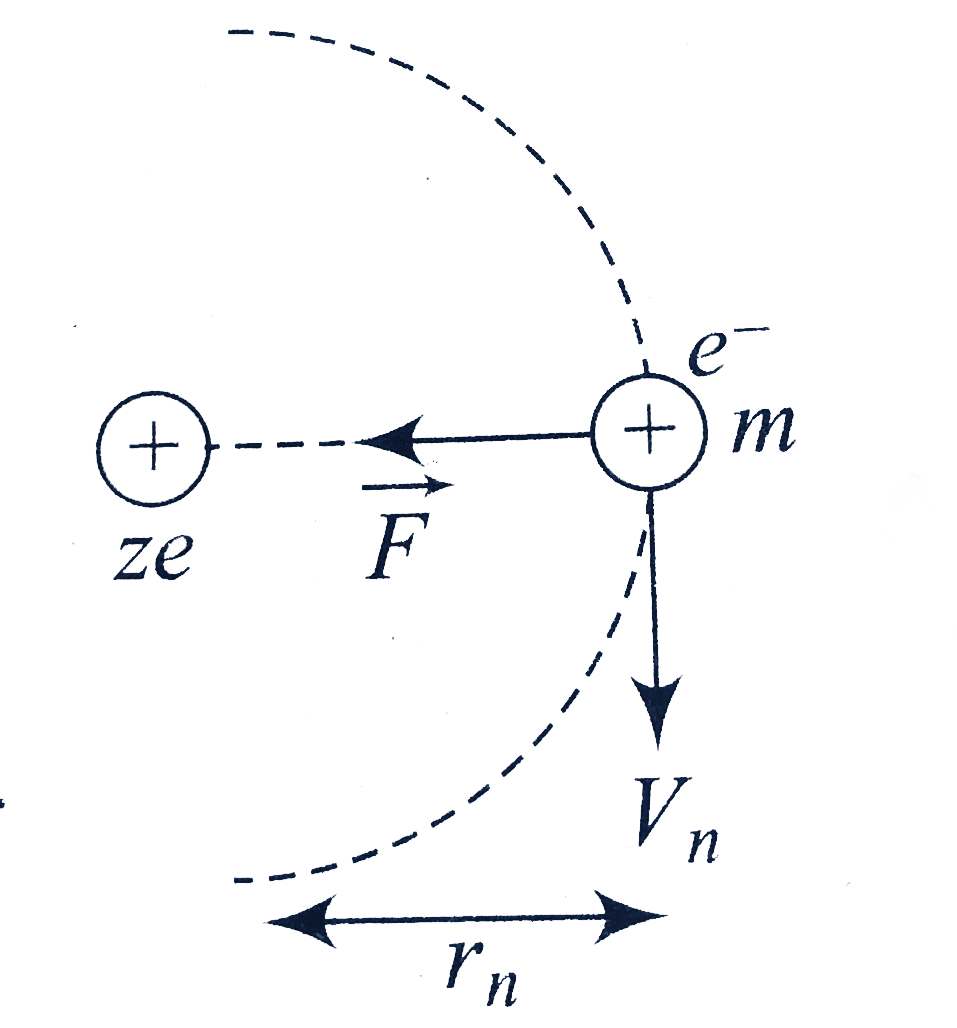
Hydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
![Hydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr = (nh//2 pi), where m = mass of the electron , v =velocity of the electron in the orbit , r =radius of the orbit , and n = 1, 2, 3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is lambda. we find that (1)/(lambda) = R [(1)/(J^(2)) - (1)/(K^(2))], where R is Rydberg's constant. On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P = 2n (h//2 pi). i.e., an even multipal of (h//2 pi). Answer the following questions regarding the other planet based on above passage: In our world, the ionization potential energy of a hydrogen atom is 13.6 eV. On the other planet, this ionization potential energy will be](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V04_C04_E01_246_Q01.png)
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the ionization potential energy of a hydrogen atom is 13.6eV. On the other planet, this ionization potential energy will be
The correct Answer is:A
On our planed En=−13.6n2
On other planet E'n=−13.6(2n)2
⇒E'n=En4=−3.4eV
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - Integer4videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - Fill In The Blanks8videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - Multiple Correct13videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - QUESTION BANK65videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMSEXERCISE - QUESTION BANK40videos
ATOMS
Similar Questions
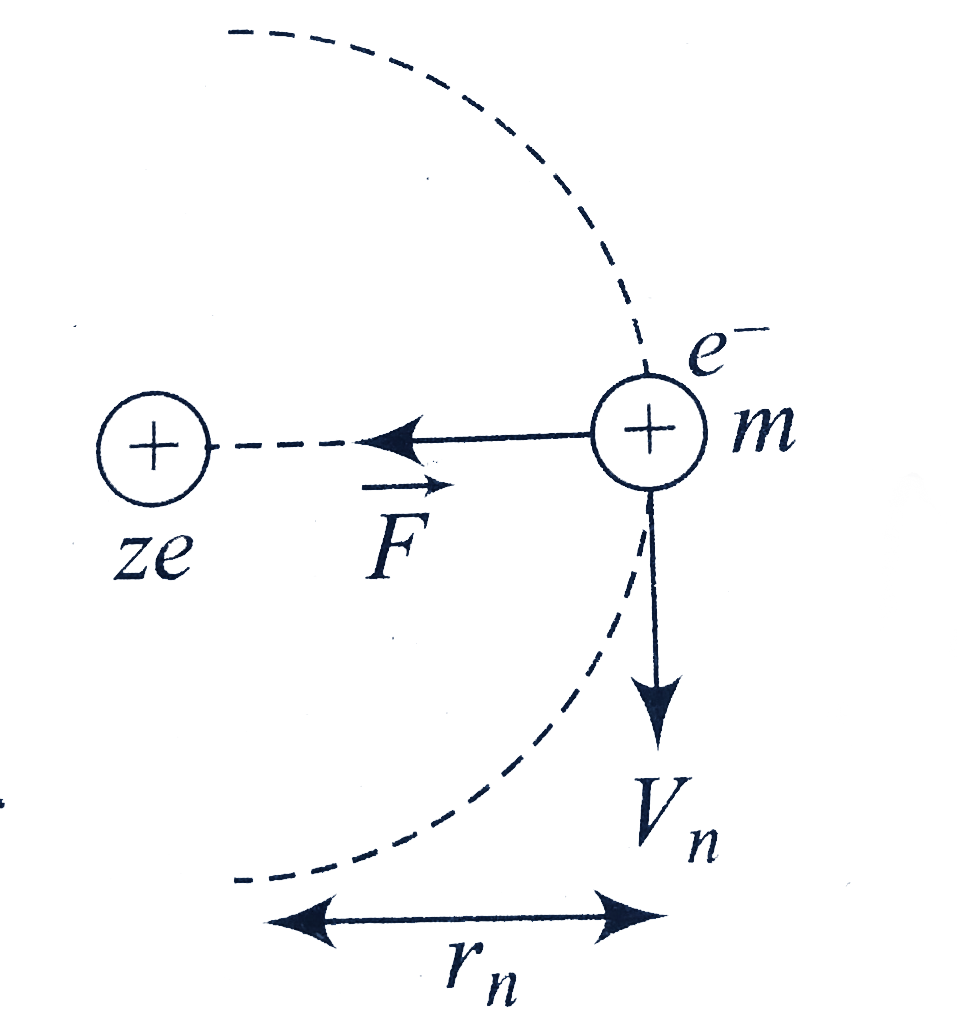
Hydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
The minimum permissible radius of the orbit will beView SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should beView Solution
Knowledge Check
- Question 1 - Select One
The angular momentum (L) of an electron in a Bohr orbit is gives as:
AL=nh2πBL=√l(l+1)h2πCL=mg2πDL=h4π - Question 2 - Select One
In Bohr's orbit angular momentum of an electron is proportional to
A√rB√r2CrDr−1/2 - Question 3 - Select One
The minimum orbital angular momentum of the electron in a hydrogen atom is
AhBh/2Ch/2πDh/λ
The angular momentum of an electron in an orbit is quantized because:
View SolutionAccording to Bohr's atomic model, electrons revolve in ______ orbits.
View SolutionAccording to Boohr's theory the angular momentum of an electron in 5th orbit is :
View SolutionThe orbital speed of an electron orbiting around the nucleus in a circular orbit of radius r is v. Then the magnetic dipole moment of the electron will be
View SolutionAccording to Boohr's theory the angular momentum of an electron in 5th orbit is :
View Solution

